Enhancing Interpretability of Sparse Latent Representations with Class Information

Variational Autoencoders (VAEs) are powerful generative models for learning latent representations. Standard VAEs generate dispersed and unstructured latent spaces by utilizing all dimensions, which limits their interpretability, especially in high-dimensional spaces. To address this challenge, Variational Sparse Coding (VSC) introduces a spike-and-slab prior distribution, resulting in sparse latent representations for each input. These sparse representations, characterized by a limited number of active dimensions, are inherently more interpretable. Despite this advantage, VSC falls short in providing structured interpretations across samples within the same class. Intuitively, samples from the same class are expected to share similar attributes while allowing for variations in those attributes. This expectation should manifest as consistent patterns of active dimensions in their latent representations, but VSC does not enforce such consistency. In this paper, we propose a novel approach to enhance the latent space interpretability by ensuring that the active dimensions in the latent space are consistent across samples within the same class. To achieve this, we introduce a new loss function that encourages samples from the same class to share similar active dimensions. This alignment creates a more structured and interpretable latent space, where each shared dimension corresponds to a high-level concept, or "factor." Unlike existing disentanglement-based methods that primarily focus on global factors shared across all classes, our method captures both global and class-specific factors, thereby enhancing the utility and interpretability of latent representations.

Crane: Context-Guided Prompt Learning and Attention Refinement for Zero-Shot Anomaly Detections

Anomaly Detection (AD) involves identifying deviations from normal data distributions and is critical in fields such as medical diagnostics and industrial defect detection. Traditional AD methods typically require the availability of normal training samples; however, this assumption is not always feasible, as collecting such data can be impractical. Additionally, these methods often struggle to generalize across different domains. Recent advancements, such as AnomalyCLIP and AdaCLIP, utilize the zero-shot generalization capabilities of CLIP but still face a performance gap between image-level and pixel-level anomaly detection. To address this gap, we propose a novel approach that conditions the prompts of the text encoder based on image context extracted from the vision encoder. Also, to capture fine-grained variations more effectively, we have modified the CLIP vision encoder and altered the extraction of dense features. These changes ensure that the features retain richer spatial and structural information for both normal and anomalous prompts. Our method achieves state-of-the-art performance, improving performance by 2% to 29% across different metrics on 14 datasets. This demonstrates its effectiveness in both image-level and pixel-level anomaly detection.

Water Flow Detection Device Based on Sound Data Analysis and Machine Learning to Detect Water Leakage

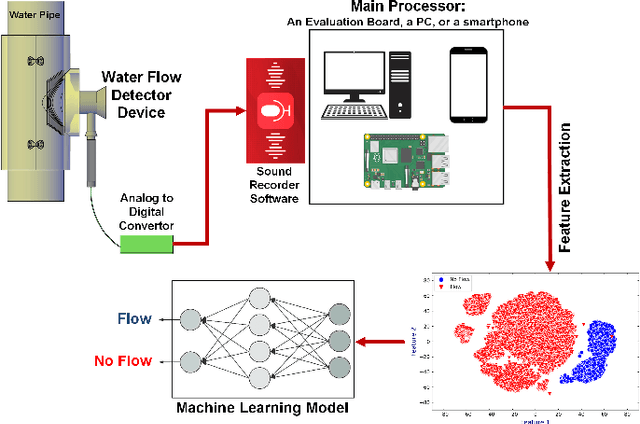
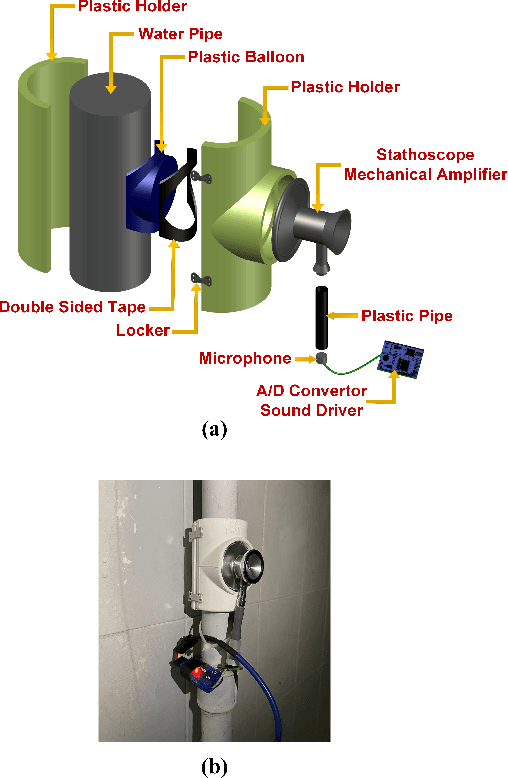
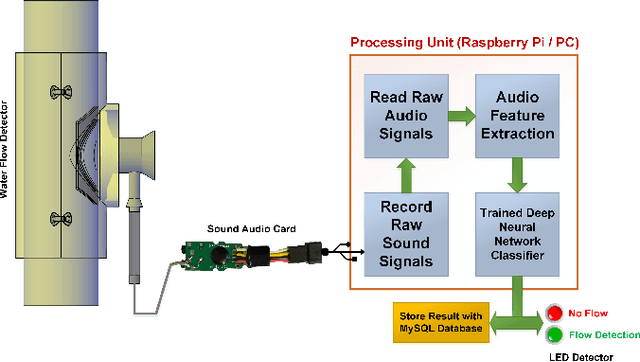
In this paper, we introduce a novel mechanism that uses machine learning techniques to detect water leaks in pipes. The proposed simple and low-cost mechanism is designed that can be easily installed on building pipes with various sizes. The system works based on gathering and amplifying water flow signals using a mechanical sound amplifier. Then sounds are recorded and converted to digital signals in order to be analyzed. After feature extraction and selection, deep neural networks are used to discriminate between with and without leak pipes. The experimental results show that this device can detect at least 100 milliliters per minute (mL/min) of water flow in a pipe so that it can be used as a core of a water leakage detection system.

Subgoal Discovery Using a Free Energy Paradigm and State Aggregations

Reinforcement learning (RL) plays a major role in solving complex sequential decision-making tasks. Hierarchical and goal-conditioned RL are promising methods for dealing with two major problems in RL, namely sample inefficiency and difficulties in reward shaping. These methods tackle the mentioned problems by decomposing a task into simpler subtasks and temporally abstracting a task in the action space. One of the key components for task decomposition of these methods is subgoal discovery. We can use the subgoal states to define hierarchies of actions and also use them in decomposing complex tasks. Under the assumption that subgoal states are more unpredictable, we propose a free energy paradigm to discover them. This is achieved by using free energy to select between two spaces, the main space and an aggregation space. The $model \; changes$ from neighboring states to a given state shows the unpredictability of a given state, and therefore it is used in this paper for subgoal discovery. Our empirical results on navigation tasks like grid-world environments show that our proposed method can be applied for subgoal discovery without prior knowledge of the task. Our proposed method is also robust to the stochasticity of environments.

Artificial Data Point Generation in Clustered Latent Space for Small Medical Datasets

One of the growing trends in machine learning is the use of data generation techniques, since the performance of machine learning models is dependent on the quantity of the training dataset. However, in many medical applications, collecting large datasets is challenging due to resource constraints, which leads to overfitting and poor generalization. This paper introduces a novel method, Artificial Data Point Generation in Clustered Latent Space (AGCL), designed to enhance classification performance on small medical datasets through synthetic data generation. The AGCL framework involves feature extraction, K-means clustering, cluster evaluation based on a class separation metric, and the generation of synthetic data points from clusters with distinct class representations. This method was applied to Parkinson's disease screening, utilizing facial expression data, and evaluated across multiple machine learning classifiers. Experimental results demonstrate that AGCL significantly improves classification accuracy compared to baseline, GN and kNNMTD. AGCL achieved the highest overall test accuracy of 83.33% and cross-validation accuracy of 90.90% in majority voting over different emotions, confirming its effectiveness in augmenting small datasets.

Out-of-distribution detection using normalizing flows on the data manifold

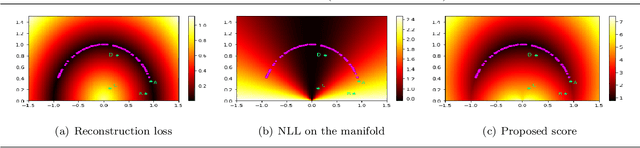
A common approach for out-of-distribution detection involves estimating an underlying data distribution, which assigns a lower likelihood value to out-of-distribution data. Normalizing flows are likelihood-based generative models providing a tractable density estimation via dimension-preserving invertible transformations. Conventional normalizing flows are prone to fail in out-of-distribution detection, because of the well-known curse of dimensionality problem of the likelihood-based models. According to the manifold hypothesis, real-world data often lie on a low-dimensional manifold. This study investigates the effect of manifold learning using normalizing flows on out-of-distribution detection. We proceed by estimating the density on a low-dimensional manifold, coupled with measuring the distance from the manifold, as criteria for out-of-distribution detection. However, individually, each of them is insufficient for this task. The extensive experimental results show that manifold learning improves the out-of-distribution detection ability of a class of likelihood-based models known as normalizing flows. This improvement is achieved without modifying the model structure or using auxiliary out-of-distribution data during training.

Combination of Single and Multi-frame Image Super-resolution: An Analytical Perspective

Super-resolution is the process of obtaining a high-resolution image from one or more low-resolution images. Single image super-resolution (SISR) and multi-frame super-resolution (MFSR) methods have been evolved almost independently for years. A neglected study in this field is the theoretical analysis of finding the optimum combination of SISR and MFSR. To fill this gap, we propose a novel theoretical analysis based on the iterative shrinkage and thresholding algorithm. We implement and compare several approaches for combining SISR and MFSR, and simulation results support the finding of our theoretical analysis, both quantitatively and qualitatively.

Efficient Relation-aware Neighborhood Aggregation in Graph Neural Networks via Tensor Decomposition

Many Graph Neural Networks (GNNs) are proposed for KG embedding. However, lots of these methods neglect the importance of the information of relations and combine it with the information of entities inefficiently and mostly additively, leading to low expressiveness. To address this issue, we introduce a general knowledge graph encoder incorporating tensor decomposition in the aggregation function of Relational Graph Convolutional Network (R-GCN). In our model, the parameters of a low-rank core projection tensor, used to transform neighbor entities, are shared across relations to benefit from multi-task learning and produce expressive relation-aware representations. Besides, we propose a low-rank estimation of the core tensor using CP decomposition to compress the model, which is also applicable, as a regularization method, to other similar GNNs. We train our model using a contrastive loss, which relieves the training limitation of the 1-N method on huge graphs. We achieved favorably competitive results on FB15-237 and WN18RR with embeddings in comparably lower dimensions; particularly, we improved R-GCN performance on FB15-237 by 36% with the same decoder.

Stochastic First-Order Learning for Large-Scale Flexibly Tied Gaussian Mixture Model

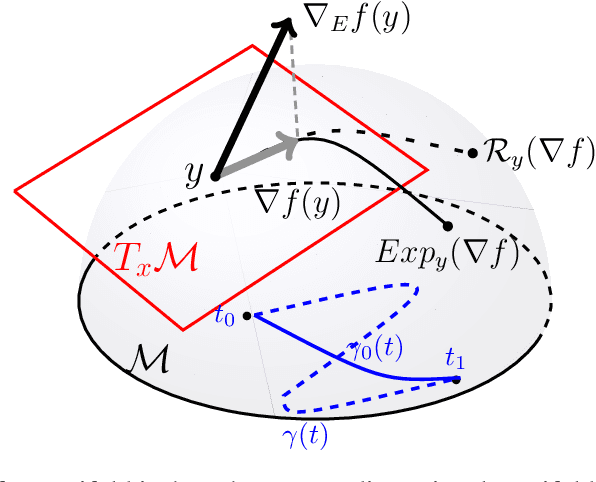
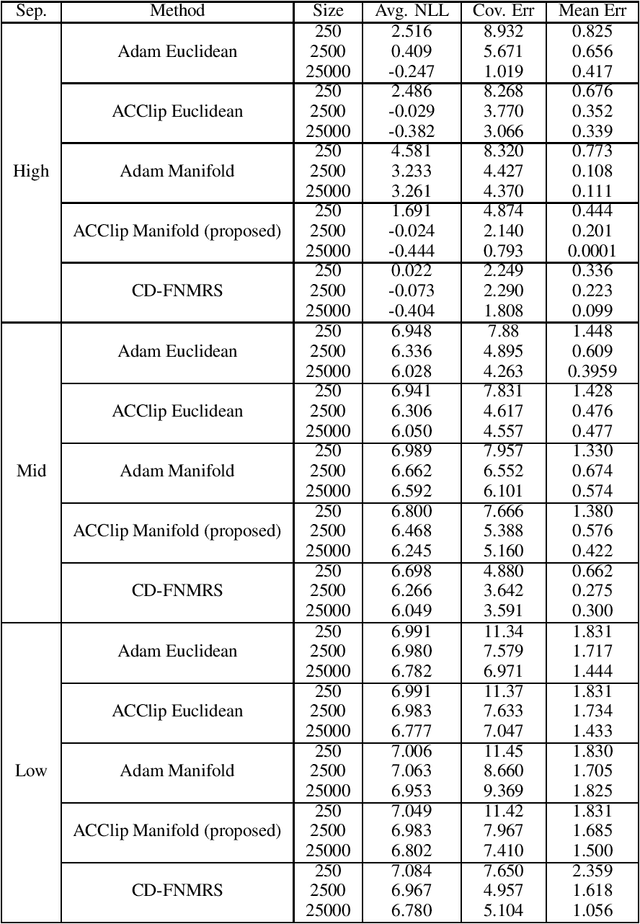
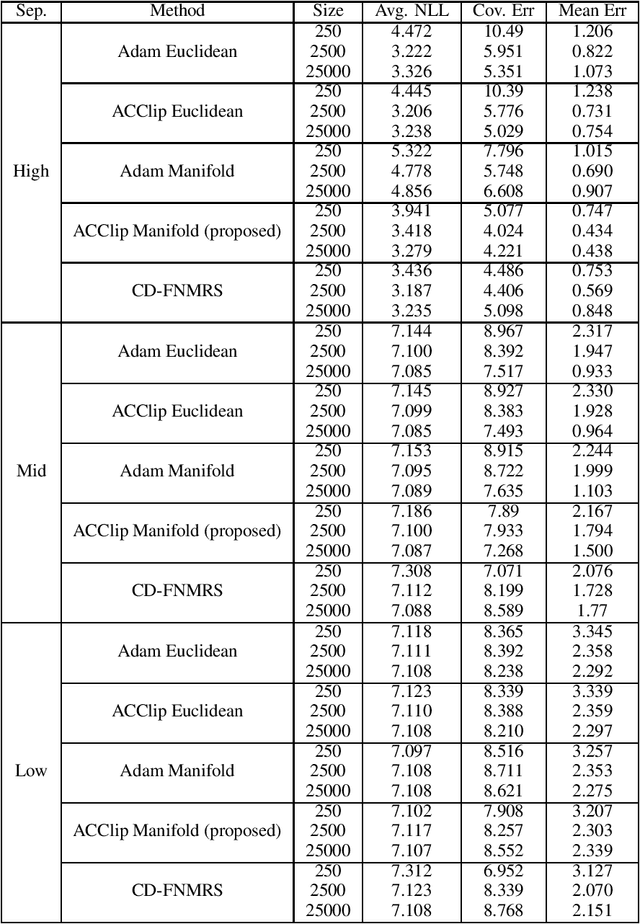
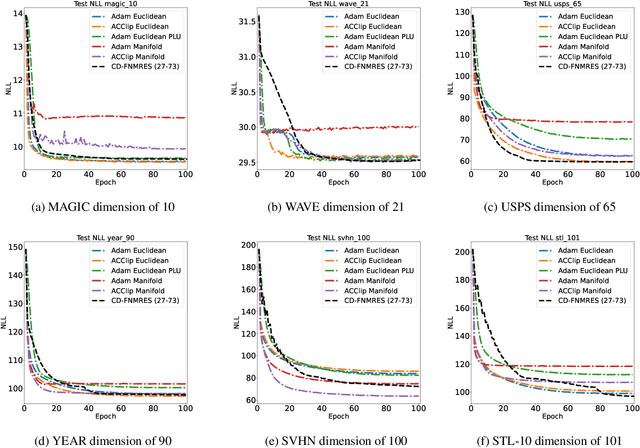
Gaussian Mixture Models (GMM) are one of the most potent parametric density estimators based on the kernel model that finds application in many scientific domains. In recent years, with the dramatic enlargement of data sources, typical machine learning algorithms, e.g. Expectation Maximization (EM), encounters difficulty with high-dimensional and streaming data. Moreover, complicated densities often demand a large number of Gaussian components. This paper proposes a fast online parameter estimation algorithm for GMM by using first-order stochastic optimization. This approach provides a framework to cope with the challenges of GMM when faced with high-dimensional streaming data and complex densities by leveraging the flexibly-tied factorization of the covariance matrix. A new stochastic Manifold optimization algorithm that preserves the orthogonality is introduced and used along with the well-known Euclidean space numerical optimization. Numerous empirical results on both synthetic and real datasets justify the effectiveness of our proposed stochastic method over EM-based methods in the sense of better-converged maximum for likelihood function, fewer number of needed epochs for convergence, and less time consumption per epoch.

Fast Online and Relational Tracking

To overcome challenges in multiple object tracking task, recent algorithms use interaction cues alongside motion and appearance features. These algorithms use graph neural networks or transformers to extract interaction features that lead to high computation costs. In this paper, a novel interaction cue based on geometric features is presented aiming to detect occlusion and re-identify lost targets with low computational cost. Moreover, in most algorithms, camera motion is considered negligible, which is a strong assumption that is not always true and leads to ID Switch or mismatching of targets. In this paper, a method for measuring camera motion and removing its effect is presented that efficiently reduces the camera motion effect on tracking. The proposed algorithm is evaluated on MOT17 and MOT20 datasets and it achieves the state-of-the-art performance of MOT17 and comparable results on MOT20. The code is also publicly available.