Seyedeh Fatemeh Razavi
Out-of-distribution detection using normalizing flows on the data manifold
Aug 26, 2023Abstract:A common approach for out-of-distribution detection involves estimating an underlying data distribution, which assigns a lower likelihood value to out-of-distribution data. Normalizing flows are likelihood-based generative models providing a tractable density estimation via dimension-preserving invertible transformations. Conventional normalizing flows are prone to fail in out-of-distribution detection, because of the well-known curse of dimensionality problem of the likelihood-based models. According to the manifold hypothesis, real-world data often lie on a low-dimensional manifold. This study investigates the effect of manifold learning using normalizing flows on out-of-distribution detection. We proceed by estimating the density on a low-dimensional manifold, coupled with measuring the distance from the manifold, as criteria for out-of-distribution detection. However, individually, each of them is insufficient for this task. The extensive experimental results show that manifold learning improves the out-of-distribution detection ability of a class of likelihood-based models known as normalizing flows. This improvement is achieved without modifying the model structure or using auxiliary out-of-distribution data during training.
Joint Manifold Learning and Density Estimation Using Normalizing Flows
Jun 07, 2022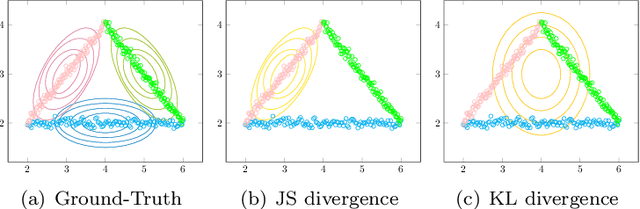
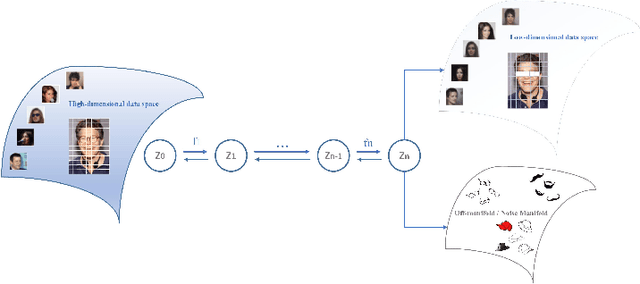

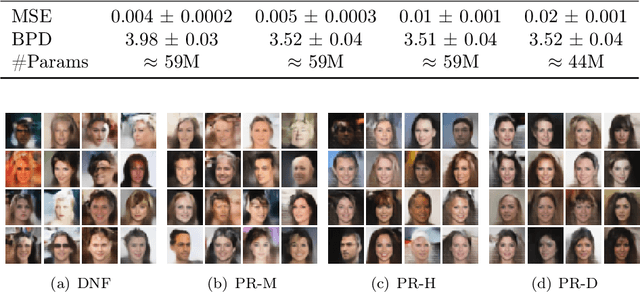
Abstract:Based on the manifold hypothesis, real-world data often lie on a low-dimensional manifold, while normalizing flows as a likelihood-based generative model are incapable of finding this manifold due to their structural constraints. So, one interesting question arises: $\textit{"Can we find sub-manifold(s) of data in normalizing flows and estimate the density of the data on the sub-manifold(s)?"}$. In this paper, we introduce two approaches, namely per-pixel penalized log-likelihood and hierarchical training, to answer the mentioned question. We propose a single-step method for joint manifold learning and density estimation by disentangling the transformed space obtained by normalizing flows to manifold and off-manifold parts. This is done by a per-pixel penalized likelihood function for learning a sub-manifold of the data. Normalizing flows assume the transformed data is Gaussianizationed, but this imposed assumption is not necessarily true, especially in high dimensions. To tackle this problem, a hierarchical training approach is employed to improve the density estimation on the sub-manifold. The results validate the superiority of the proposed methods in simultaneous manifold learning and density estimation using normalizing flows in terms of generated image quality and likelihood.
PerSpeechNorm: A Persian Toolkit for Speech Processing Normalization
Nov 01, 2021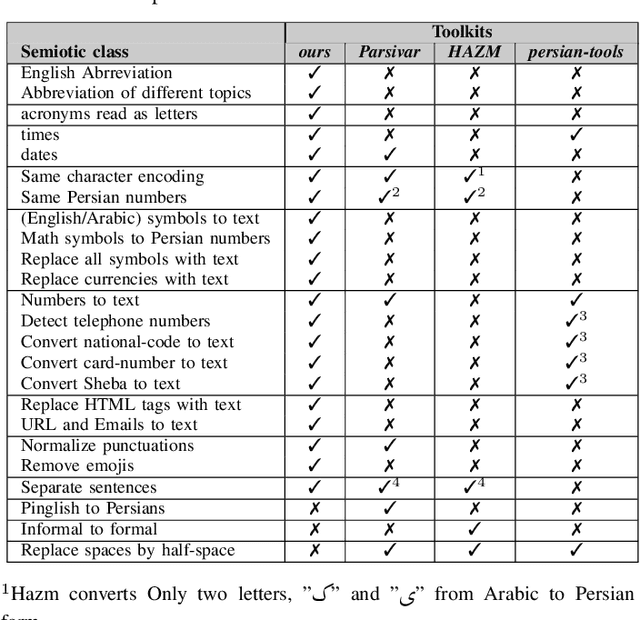

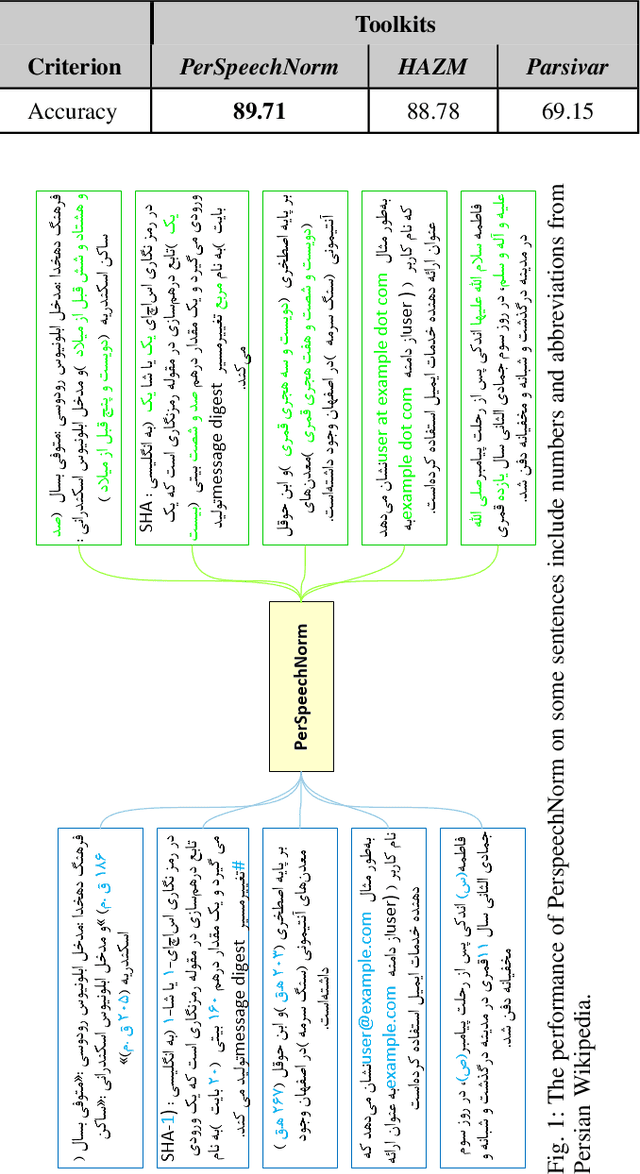
Abstract:In general, speech processing models consist of a language model along with an acoustic model. Regardless of the language model's complexity and variants, three critical pre-processing steps are needed in language models: cleaning, normalization, and tokenization. Among mentioned steps, the normalization step is so essential to format unification in pure textual applications. However, for embedded language models in speech processing modules, normalization is not limited to format unification. Moreover, it has to convert each readable symbol, number, etc., to how they are pronounced. To the best of our knowledge, there is no Persian normalization toolkits for embedded language models in speech processing modules, So in this paper, we propose an open-source normalization toolkit for text processing in speech applications. Briefly, we consider different readable Persian text like symbols (common currencies, #, @, URL, etc.), numbers (date, time, phone number, national code, etc.), and so on. Comparison with other available Persian textual normalization tools indicates the superiority of the proposed method in speech processing. Also, comparing the model's performance for one of the proposed functions (sentence separation) with other common natural language libraries such as HAZM and Parsivar indicates the proper performance of the proposed method. Besides, its evaluation of some Persian Wikipedia data confirms the proper performance of the proposed method.
FRMDN: Flow-based Recurrent Mixture Density Network
Aug 05, 2020



Abstract:Recurrent Mixture Density Networks (RMDNs) are consisted of two main parts: a Recurrent Neural Network (RNN) and a Gaussian Mixture Model (GMM), in which a kind of RNN (almost LSTM) is used to find the parameters of a GMM in every time step. While available RMDNs have been faced with different difficulties. The most important of them is high$-$dimensional problems. Since estimating the covariance matrix for the high$-$dimensional problems is more difficult, due to existing correlation between dimensions and satisfying the positive definition condition. Consequently, the available methods have usually used RMDN with a diagonal covariance matrix for high$-$dimensional problems by supposing independence among dimensions. Hence, in this paper with inspiring a common approach in the literature of GMM, we consider a tied configuration for each precision matrix (inverse of the covariance matrix) in RMDN as $(\(\Sigma _k^{ - 1} = U{D_k}U\))$ to enrich GMM rather than considering a diagonal form for it. But due to simplicity, we assume $\(U\)$ be an Identity matrix and $\(D_k\)$ is a specific diagonal matrix for $\(k^{th}\)$ component. Until now, we only have a diagonal matrix and it does not differ with available diagonal RMDNs. Besides, Flow$-$based neural networks are a new group of generative models that are able to transform a distribution to a simpler distribution and vice versa, through a sequence of invertible functions. Therefore, we applied a diagonal GMM on transformed observations. At every time step, the next observation, $\({y_{t + 1}}\)$, has been passed through a flow$-$based neural network to obtain a much simpler distribution. Experimental results for a reinforcement learning problem verify the superiority of the proposed method to the base$-$line method in terms of Negative Log$-$Likelihood (NLL) for RMDN and the cumulative reward for a controller with fewer population size.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge