Out-of-distribution detection using normalizing flows on the data manifold

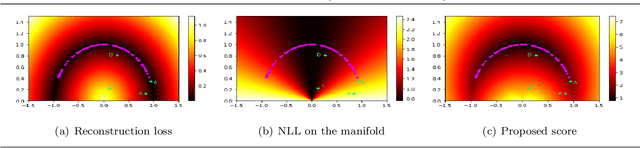
A common approach for out-of-distribution detection involves estimating an underlying data distribution, which assigns a lower likelihood value to out-of-distribution data. Normalizing flows are likelihood-based generative models providing a tractable density estimation via dimension-preserving invertible transformations. Conventional normalizing flows are prone to fail in out-of-distribution detection, because of the well-known curse of dimensionality problem of the likelihood-based models. According to the manifold hypothesis, real-world data often lie on a low-dimensional manifold. This study investigates the effect of manifold learning using normalizing flows on out-of-distribution detection. We proceed by estimating the density on a low-dimensional manifold, coupled with measuring the distance from the manifold, as criteria for out-of-distribution detection. However, individually, each of them is insufficient for this task. The extensive experimental results show that manifold learning improves the out-of-distribution detection ability of a class of likelihood-based models known as normalizing flows. This improvement is achieved without modifying the model structure or using auxiliary out-of-distribution data during training.

Revealing Model Biases: Assessing Deep Neural Networks via Recovered Sample Analysis

This paper proposes a straightforward and cost-effective approach to assess whether a deep neural network (DNN) relies on the primary concepts of training samples or simply learns discriminative, yet simple and irrelevant features that can differentiate between classes. The paper highlights that DNNs, as discriminative classifiers, often find the simplest features to discriminate between classes, leading to a potential bias towards irrelevant features and sometimes missing generalization. While a generalization test is one way to evaluate a trained model's performance, it can be costly and may not cover all scenarios to ensure that the model has learned the primary concepts. Furthermore, even after conducting a generalization test, identifying bias in the model may not be possible. Here, the paper proposes a method that involves recovering samples from the parameters of the trained model and analyzing the reconstruction quality. We believe that if the model's weights are optimized to discriminate based on some features, these features will be reflected in the reconstructed samples. If the recovered samples contain the primary concepts of the training data, it can be concluded that the model has learned the essential and determining features. On the other hand, if the recovered samples contain irrelevant features, it can be concluded that the model is biased towards these features. The proposed method does not require any test or generalization samples, only the parameters of the trained model and the training data that lie on the margin. Our experiments demonstrate that the proposed method can determine whether the model has learned the desired features of the training data. The paper highlights that our understanding of how these models work is limited, and the proposed approach addresses this issue.

Joint Manifold Learning and Density Estimation Using Normalizing Flows

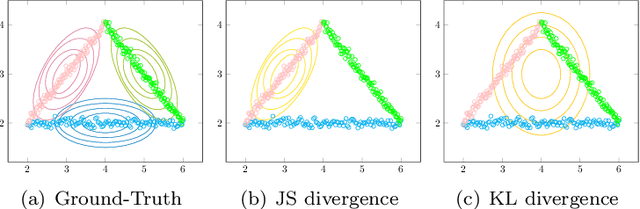
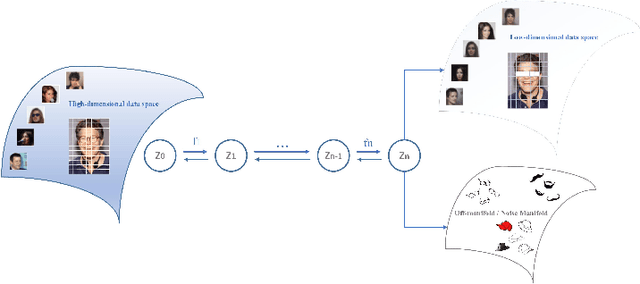
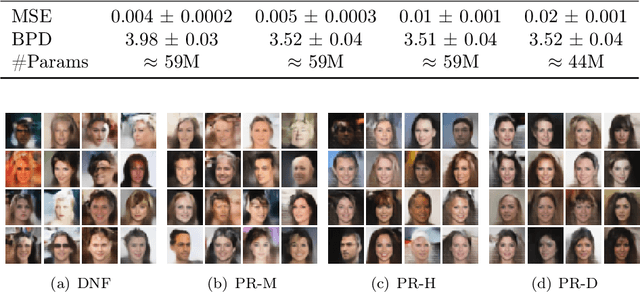
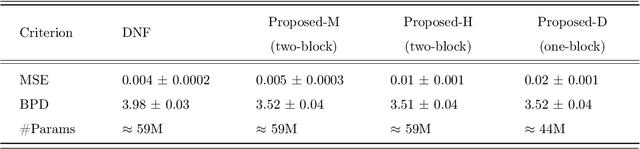
Based on the manifold hypothesis, real-world data often lie on a low-dimensional manifold, while normalizing flows as a likelihood-based generative model are incapable of finding this manifold due to their structural constraints. So, one interesting question arises: $\textit{"Can we find sub-manifold(s) of data in normalizing flows and estimate the density of the data on the sub-manifold(s)?"}$. In this paper, we introduce two approaches, namely per-pixel penalized log-likelihood and hierarchical training, to answer the mentioned question. We propose a single-step method for joint manifold learning and density estimation by disentangling the transformed space obtained by normalizing flows to manifold and off-manifold parts. This is done by a per-pixel penalized likelihood function for learning a sub-manifold of the data. Normalizing flows assume the transformed data is Gaussianizationed, but this imposed assumption is not necessarily true, especially in high dimensions. To tackle this problem, a hierarchical training approach is employed to improve the density estimation on the sub-manifold. The results validate the superiority of the proposed methods in simultaneous manifold learning and density estimation using normalizing flows in terms of generated image quality and likelihood.