Fast Online and Relational Tracking

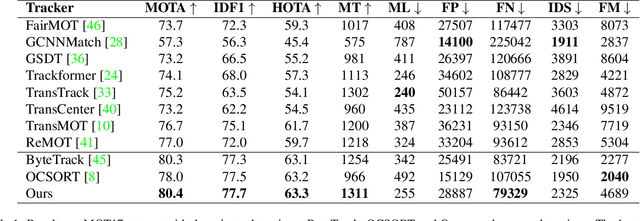
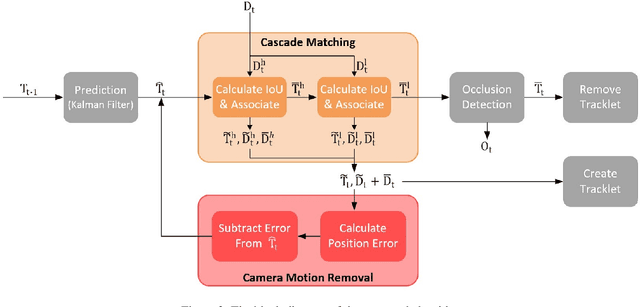
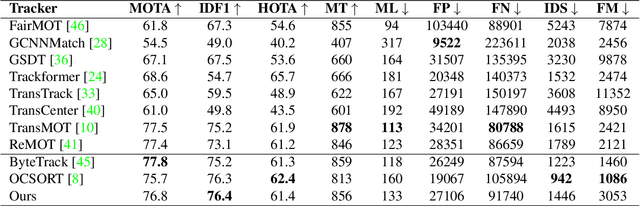
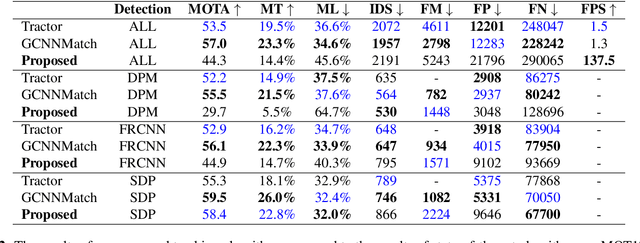
To overcome challenges in multiple object tracking task, recent algorithms use interaction cues alongside motion and appearance features. These algorithms use graph neural networks or transformers to extract interaction features that lead to high computation costs. In this paper, a novel interaction cue based on geometric features is presented aiming to detect occlusion and re-identify lost targets with low computational cost. Moreover, in most algorithms, camera motion is considered negligible, which is a strong assumption that is not always true and leads to ID Switch or mismatching of targets. In this paper, a method for measuring camera motion and removing its effect is presented that efficiently reduces the camera motion effect on tracking. The proposed algorithm is evaluated on MOT17 and MOT20 datasets and it achieves the state-of-the-art performance of MOT17 and comparable results on MOT20. The code is also publicly available.

Simple online and real-time tracking with occlusion handling

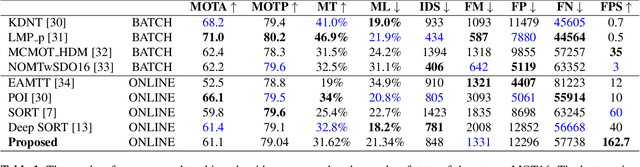
Multiple object tracking is a challenging problem in computer vision due to difficulty in dealing with motion prediction, occlusion handling, and object re-identification. Many recent algorithms use motion and appearance cues to overcome these challenges. But using appearance cues increases the computation cost notably and therefore the speed of the algorithm decreases significantly which makes them inappropriate for online applications. In contrast, there are algorithms that only use motion cues to increase speed, especially for online applications. But these algorithms cannot handle occlusions and re-identify lost objects. In this paper, a novel online multiple object tracking algorithm is presented that only uses geometric cues of objects to tackle the occlusion and reidentification challenges simultaneously. As a result, it decreases the identity switch and fragmentation metrics. Experimental results show that the proposed algorithm could decrease identity switch by 40% and fragmentation by 28% compared to the state of the art online tracking algorithms. The code is also publicly available.