Stochastic First-Order Learning for Large-Scale Flexibly Tied Gaussian Mixture Model

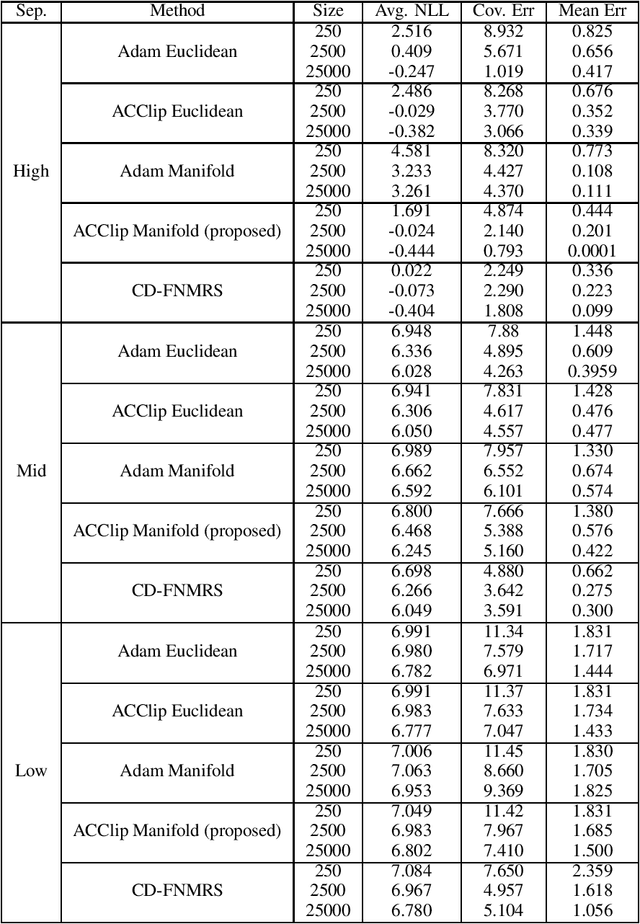
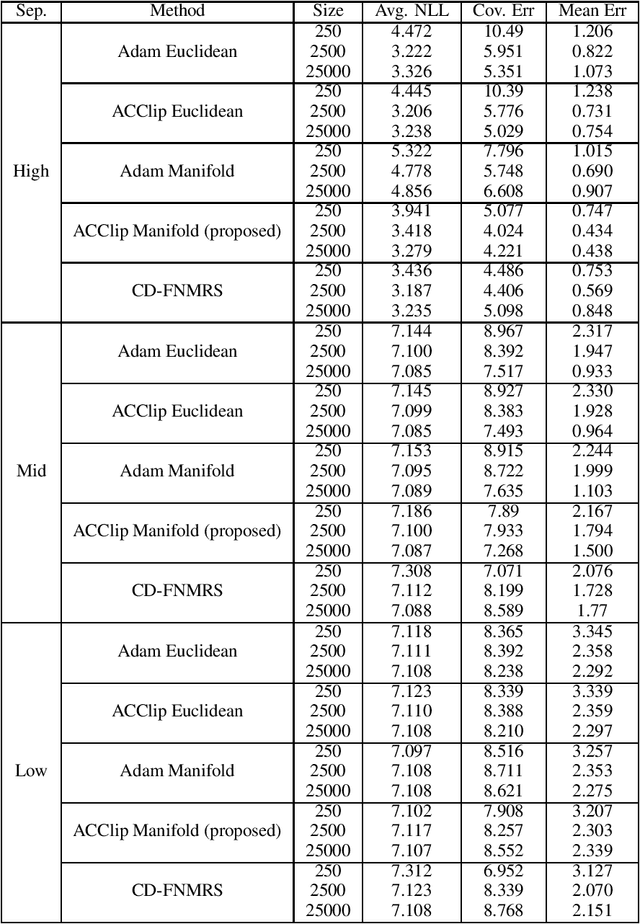
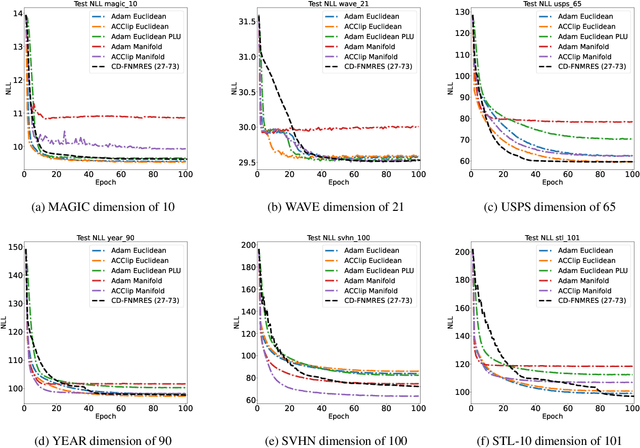
Gaussian Mixture Models (GMM) are one of the most potent parametric density estimators based on the kernel model that finds application in many scientific domains. In recent years, with the dramatic enlargement of data sources, typical machine learning algorithms, e.g. Expectation Maximization (EM), encounters difficulty with high-dimensional and streaming data. Moreover, complicated densities often demand a large number of Gaussian components. This paper proposes a fast online parameter estimation algorithm for GMM by using first-order stochastic optimization. This approach provides a framework to cope with the challenges of GMM when faced with high-dimensional streaming data and complex densities by leveraging the flexibly-tied factorization of the covariance matrix. A new stochastic Manifold optimization algorithm that preserves the orthogonality is introduced and used along with the well-known Euclidean space numerical optimization. Numerous empirical results on both synthetic and real datasets justify the effectiveness of our proposed stochastic method over EM-based methods in the sense of better-converged maximum for likelihood function, fewer number of needed epochs for convergence, and less time consumption per epoch.