Clustering in Partially Labeled Stochastic Block Models via Total Variation Minimization
Paper and Code
Nov 03, 2019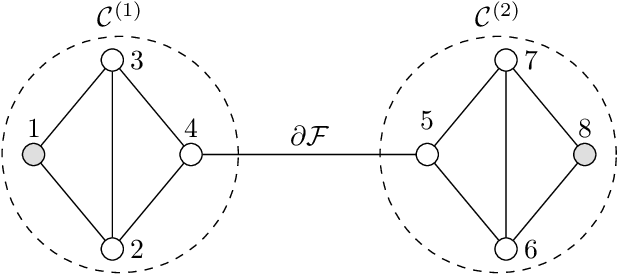
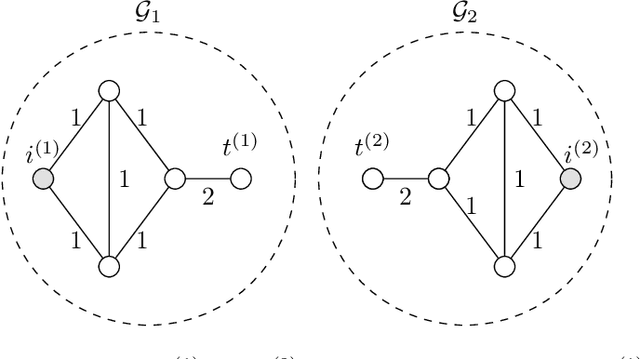
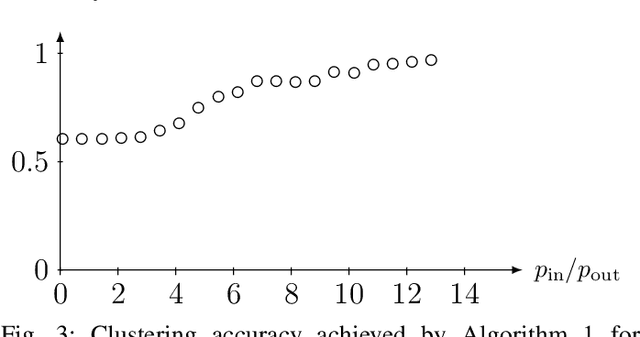
A main task in data analysis is to organize data points into coherent groups or clusters. The stochastic block model is a probabilistic model for the cluster structure. This model prescribes different probabilities for the presence of edges within a cluster and between different clusters. We assume that the cluster assignments are known for at least one data point in each cluster. In such a partially labeled stochastic block model, clustering amounts to estimating the cluster assignments of the remaining data points. We study total variation minimization as a method for this clustering task. We implement the resulting clustering algorithm as a highly scalable message passing protocol. We also provide a condition on the model parameters such that total variation minimization allows for accurate clustering.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge