Local Graph Clustering with Network Lasso

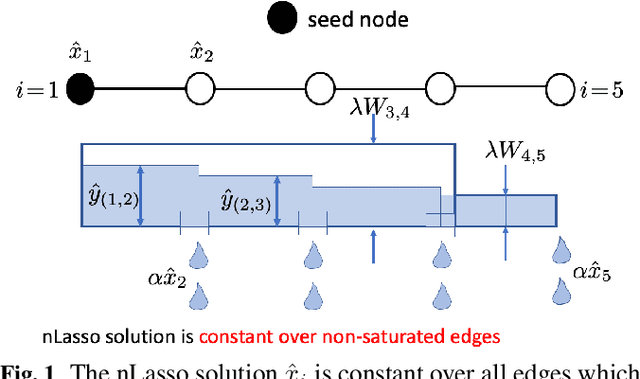
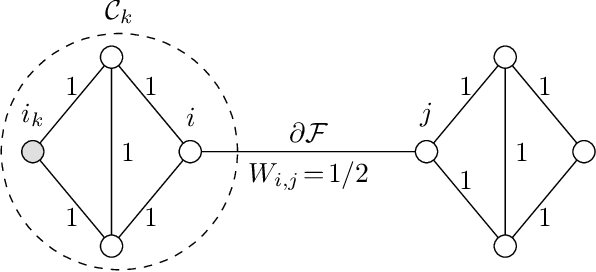
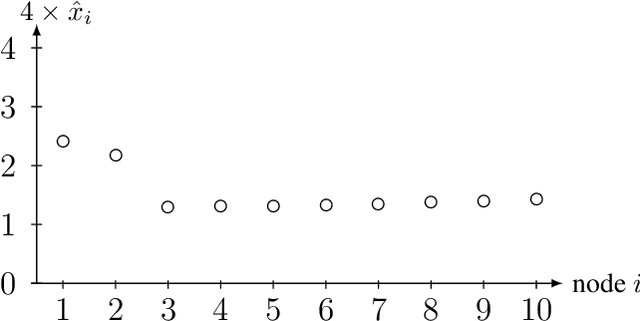
We study the statistical and computational properties of a network Lasso method for local graph clustering. The clusters delivered by nLasso can be characterized elegantly via network flows between cluster boundary and seed nodes. While spectral clustering methods are guided by a minimization of the graph Laplacian quadratic form, nLasso minimizes the total variation of cluster indicator signals. As demonstrated theoretically and numerically, nLasso methods can handle very sparse clusters (chain-like) which are difficult for spectral clustering. We also verify that a primal-dual method for non-smooth optimization allows to approximate nLasso solutions with optimal worst-case convergence rate.