Linli Zhang
Networked Federated Multi-Task Learning
May 26, 2021
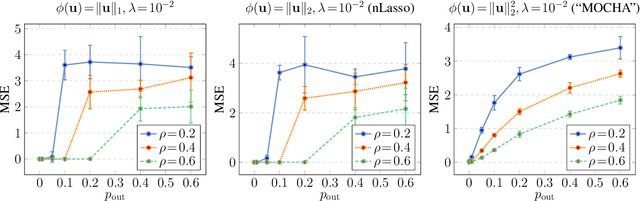
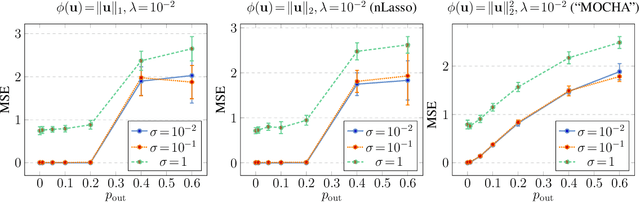
Abstract:Many important application domains generate distributed collections of heterogeneous local datasets. These local datasets are often related via an intrinsic network structure that arises from domain-specific notions of similarity between local datasets. Different notions of similarity are induced by spatiotemporal proximity, statistical dependencies, or functional relations. We use this network structure to adaptively pool similar local datasets into nearly homogenous training sets for learning tailored models. Our main conceptual contribution is to formulate networked federated learning using the concept of generalized total variation (GTV) minimization as a regularizer. This formulation is highly flexible and can be combined with almost any parametric model including Lasso or deep neural networks. We unify and considerably extend some well-known approaches to federated multi-task learning. Our main algorithmic contribution is a novel federated learning algorithm that is well suited for distributed computing environments such as edge computing over wireless networks. This algorithm is robust against model misspecification and numerical errors arising from limited computational resources including processing time or wireless channel bandwidth. As our main technical contribution, we offer precise conditions on the local models as well on their network structure such that our algorithm learns nearly optimal local models. Our analysis reveals an interesting interplay between the (information-) geometry of local models and the (cluster-) geometry of their network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge