Meta-Dynamical State Space Models for Integrative Neural Data Analysis

Learning shared structure across environments facilitates rapid learning and adaptive behavior in neural systems. This has been widely demonstrated and applied in machine learning to train models that are capable of generalizing to novel settings. However, there has been limited work exploiting the shared structure in neural activity during similar tasks for learning latent dynamics from neural recordings. Existing approaches are designed to infer dynamics from a single dataset and cannot be readily adapted to account for statistical heterogeneities across recordings. In this work, we hypothesize that similar tasks admit a corresponding family of related solutions and propose a novel approach for meta-learning this solution space from task-related neural activity of trained animals. Specifically, we capture the variabilities across recordings on a low-dimensional manifold which concisely parametrizes this family of dynamics, thereby facilitating rapid learning of latent dynamics given new recordings. We demonstrate the efficacy of our approach on few-shot reconstruction and forecasting of synthetic dynamical systems, and neural recordings from the motor cortex during different arm reaching tasks.

Representational dissimilarity metric spaces for stochastic neural networks

Quantifying similarity between neural representations -- e.g. hidden layer activation vectors -- is a perennial problem in deep learning and neuroscience research. Existing methods compare deterministic responses (e.g. artificial networks that lack stochastic layers) or averaged responses (e.g., trial-averaged firing rates in biological data). However, these measures of deterministic representational similarity ignore the scale and geometric structure of noise, both of which play important roles in neural computation. To rectify this, we generalize previously proposed shape metrics (Williams et al. 2021) to quantify differences in stochastic representations. These new distances satisfy the triangle inequality, and thus can be used as a rigorous basis for many supervised and unsupervised analyses. Leveraging this novel framework, we find that the stochastic geometries of neurobiological representations of oriented visual gratings and naturalistic scenes respectively resemble untrained and trained deep network representations. Further, we are able to more accurately predict certain network attributes (e.g. training hyperparameters) from its position in stochastic (versus deterministic) shape space.

BAM: Bayes with Adaptive Memory

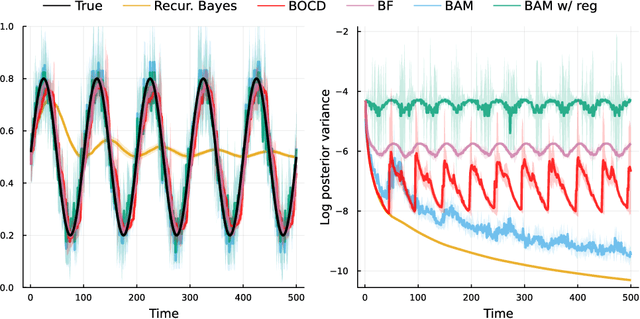
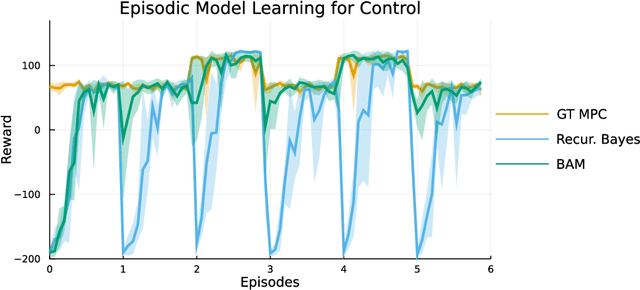
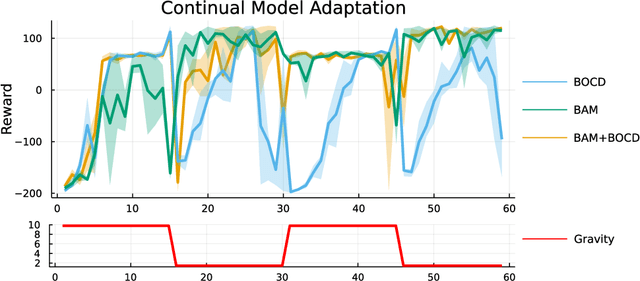
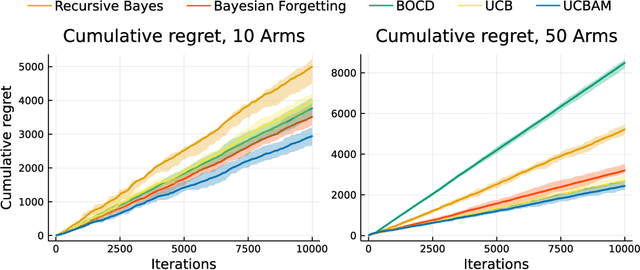
Online learning via Bayes' theorem allows new data to be continuously integrated into an agent's current beliefs. However, a naive application of Bayesian methods in non stationary environments leads to slow adaptation and results in state estimates that may converge confidently to the wrong parameter value. A common solution when learning in changing environments is to discard/downweight past data; however, this simple mechanism of "forgetting" fails to account for the fact that many real-world environments involve revisiting similar states. We propose a new framework, Bayes with Adaptive Memory (BAM), that takes advantage of past experience by allowing the agent to choose which past observations to remember and which to forget. We demonstrate that BAM generalizes many popular Bayesian update rules for non-stationary environments. Through a variety of experiments, we demonstrate the ability of BAM to continuously adapt in an ever-changing world.

On 1/n neural representation and robustness

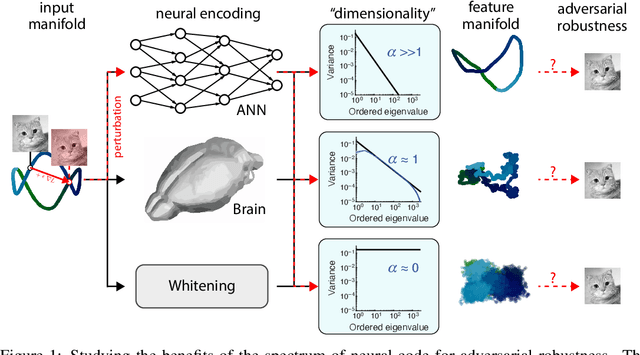
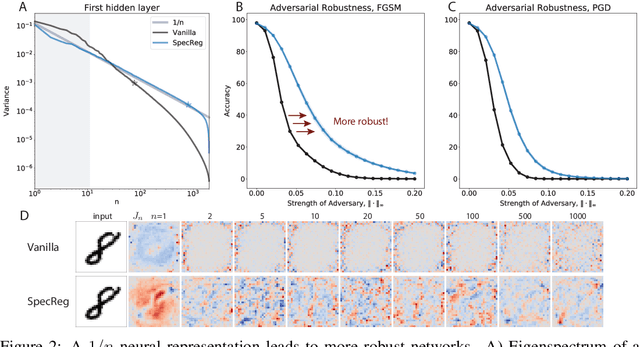
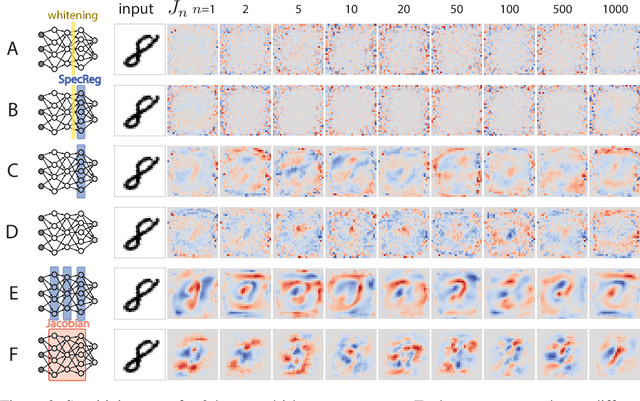
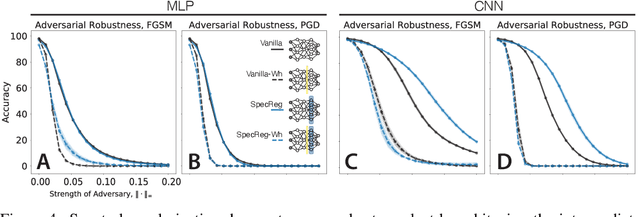
Understanding the nature of representation in neural networks is a goal shared by neuroscience and machine learning. It is therefore exciting that both fields converge not only on shared questions but also on similar approaches. A pressing question in these areas is understanding how the structure of the representation used by neural networks affects both their generalization, and robustness to perturbations. In this work, we investigate the latter by juxtaposing experimental results regarding the covariance spectrum of neural representations in the mouse V1 (Stringer et al) with artificial neural networks. We use adversarial robustness to probe Stringer et al's theory regarding the causal role of a 1/n covariance spectrum. We empirically investigate the benefits such a neural code confers in neural networks, and illuminate its role in multi-layer architectures. Our results show that imposing the experimentally observed structure on artificial neural networks makes them more robust to adversarial attacks. Moreover, our findings complement the existing theory relating wide neural networks to kernel methods, by showing the role of intermediate representations.

Streaming Variational Monte Carlo

Nonlinear state-space models are powerful tools to describe dynamical structures in complex time series. In a streaming setting where data are processed one sample at a time, simultaneously inferring the state and their nonlinear dynamics has posed significant challenges in practice. We develop a novel online learning framework, leveraging variational inference and sequential Monte Carlo, which enables flexible and accurate Bayesian joint filtering. Our method provides a filtering posterior arbitrarily close to the true filtering distribution for a wide class of dynamics models and observation models. Specifically, the proposed framework can efficiently infer a posterior over the dynamics using sparse Gaussian processes. Constant time complexity per sample makes our approach amenable to online learning scenarios and suitable for real-time applications.

Tree-Structured Recurrent Switching Linear Dynamical Systems for Multi-Scale Modeling

Many real-world systems studied are governed by complex, nonlinear dynamics. By modeling these dynamics, we can gain insight into how these systems work, make predictions about how they will behave, and develop strategies for controlling them. While there are many methods for modeling nonlinear dynamical systems, existing techniques face a trade off between offering interpretable descriptions and making accurate predictions. Here, we develop a class of models that aims to achieve both simultaneously, smoothly interpolating between simple descriptions and more complex, yet also more accurate models. Our probabilistic model achieves this multi-scale property through a hierarchy of locally linear dynamics that jointly approximate global nonlinear dynamics. We call it the tree-structured recurrent switching linear dynamical system. To fit this model, we present a fully-Bayesian sampling procedure using Polya-Gamma data augmentation to allow for fast and conjugate Gibbs sampling. Through a variety of synthetic and real examples, we show how these models outperform existing methods in both interpretability and predictive capability.