Guillermo Martín-Sánchez
Back to the Continuous Attractor
Jul 31, 2024



Abstract:Continuous attractors offer a unique class of solutions for storing continuous-valued variables in recurrent system states for indefinitely long time intervals. Unfortunately, continuous attractors suffer from severe structural instability in general--they are destroyed by most infinitesimal changes of the dynamical law that defines them. This fragility limits their utility especially in biological systems as their recurrent dynamics are subject to constant perturbations. We observe that the bifurcations from continuous attractors in theoretical neuroscience models display various structurally stable forms. Although their asymptotic behaviors to maintain memory are categorically distinct, their finite-time behaviors are similar. We build on the persistent manifold theory to explain the commonalities between bifurcations from and approximations of continuous attractors. Fast-slow decomposition analysis uncovers the persistent manifold that survives the seemingly destructive bifurcation. Moreover, recurrent neural networks trained on analog memory tasks display approximate continuous attractors with predicted slow manifold structures. Therefore, continuous attractors are functionally robust and remain useful as a universal analogy for understanding analog memory.
A Taxonomy of Recurrent Learning Rules
Jul 23, 2022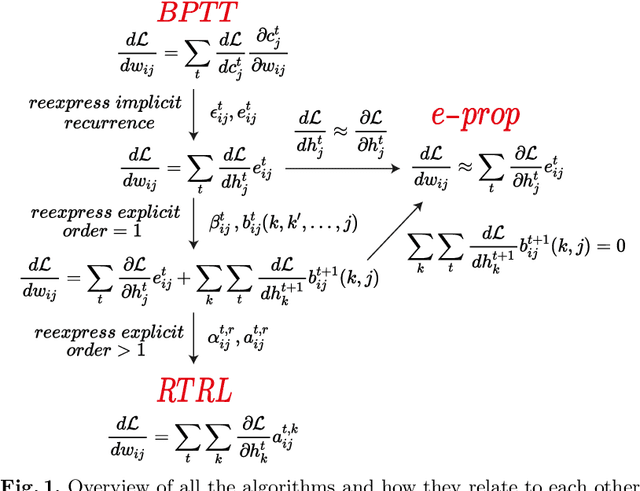
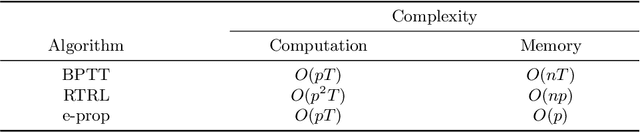
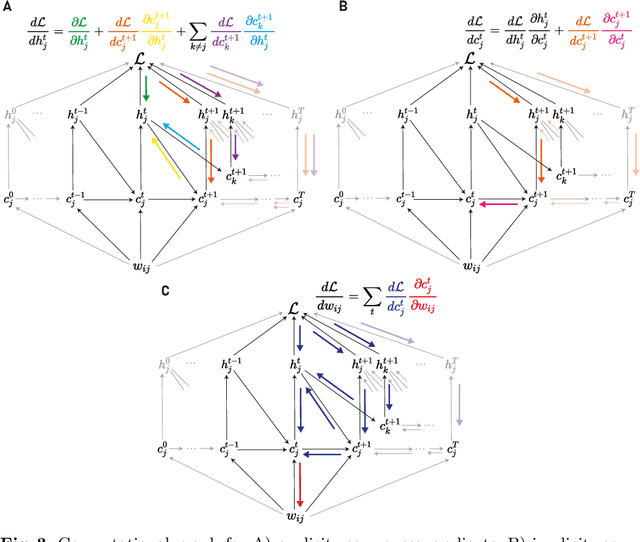
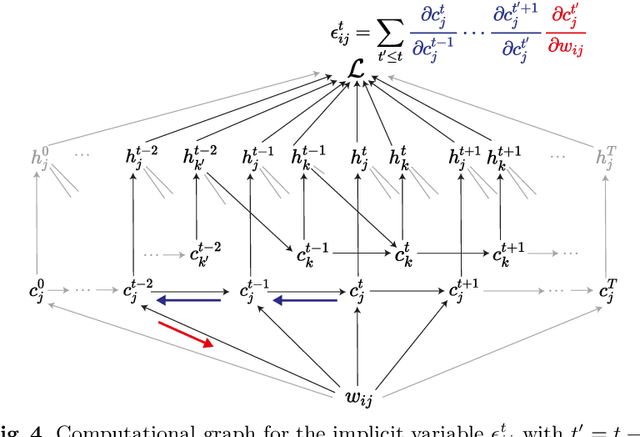
Abstract:Backpropagation through time (BPTT) is the de facto standard for training recurrent neural networks (RNNs), but it is non-causal and non-local. Real-time recurrent learning is a causal alternative, but it is highly inefficient. Recently, e-prop was proposed as a causal, local, and efficient practical alternative to these algorithms, providing an approximation of the exact gradient by radically pruning the recurrent dependencies carried over time. Here, we derive RTRL from BPTT using a detailed notation bringing intuition and clarification to how they are connected. Furthermore, we frame e-prop within in the picture, formalising what it approximates. Finally, we derive a family of algorithms of which e-prop is a special case.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge