Flexible inference of learning rules from de novo learning data using neural networks

Understanding how animals learn is a central challenge in neuroscience, with growing relevance to the development of animal- or human-aligned artificial intelligence. However, most existing approaches assume specific parametric forms for the learning rule (e.g., Q-learning, policy gradient) or are limited to simplified settings like bandit tasks, which do not involve learning a new input-output mapping from scratch. In contrast, animals must often learn new behaviors de novo, which poses a rich challenge for learning-rule inference. We target this problem by inferring learning rules directly from animal decision-making data during de novo task learning, a setting that requires models flexible enough to capture suboptimality, history dependence, and rich external stimulus integration without strong structural priors. We first propose a nonparametric framework that parameterizes the per-trial update of policy weights with a deep neural network (DNN), and validate it by recovering ground-truth rules in simulation. We then extend to a recurrent variant (RNN) that captures non-Markovian dynamics by allowing updates to depend on trial history. Applied to a large behavioral dataset of mice learning a sensory decision-making task over multiple weeks, our models improved predictions on held-out data. The inferred rules revealed asymmetric updates after correct versus error trials and history dependence, consistent with non-Markovian learning. Overall, these results introduce a flexible framework for inferring biological learning rules from behavioral data in de novo learning tasks, providing insights to inform experimental training protocols and the development of behavioral digital twins.

Modeling Neural Activity with Conditionally Linear Dynamical Systems

Neural population activity exhibits complex, nonlinear dynamics, varying in time, over trials, and across experimental conditions. Here, we develop Conditionally Linear Dynamical System (CLDS) models as a general-purpose method to characterize these dynamics. These models use Gaussian Process (GP) priors to capture the nonlinear dependence of circuit dynamics on task and behavioral variables. Conditioned on these covariates, the data is modeled with linear dynamics. This allows for transparent interpretation and tractable Bayesian inference. We find that CLDS models can perform well even in severely data-limited regimes (e.g. one trial per condition) due to their Bayesian formulation and ability to share statistical power across nearby task conditions. In example applications, we apply CLDS to model thalamic neurons that nonlinearly encode heading direction and to model motor cortical neurons during a cued reaching task

Comparing noisy neural population dynamics using optimal transport distances

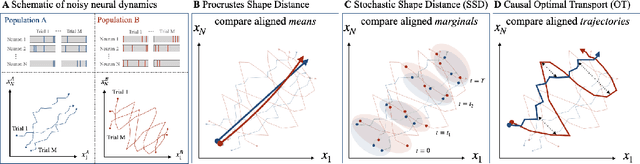
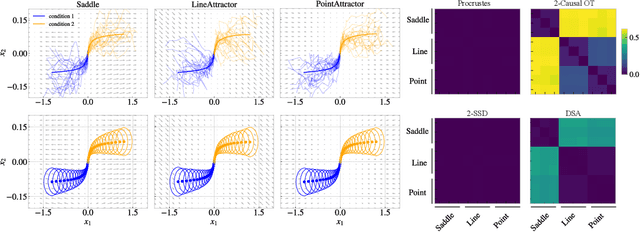
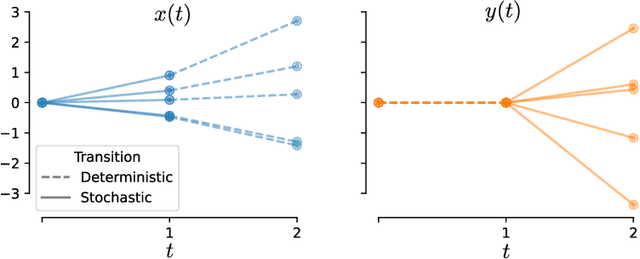
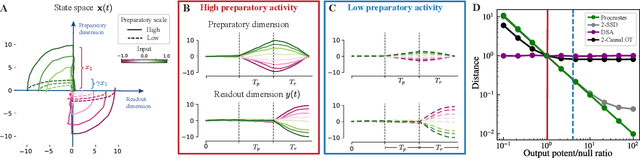
Biological and artificial neural systems form high-dimensional neural representations that underpin their computational capabilities. Methods for quantifying geometric similarity in neural representations have become a popular tool for identifying computational principles that are potentially shared across neural systems. These methods generally assume that neural responses are deterministic and static. However, responses of biological systems, and some artificial systems, are noisy and dynamically unfold over time. Furthermore, these characteristics can have substantial influence on a system's computational capabilities. Here, we demonstrate that existing metrics can fail to capture key differences between neural systems with noisy dynamic responses. We then propose a metric for comparing the geometry of noisy neural trajectories, which can be derived as an optimal transport distance between Gaussian processes. We use the metric to compare models of neural responses in different regions of the motor system and to compare the dynamics of latent diffusion models for text-to-image synthesis.

Advantages of biologically-inspired adaptive neural activation in RNNs during learning

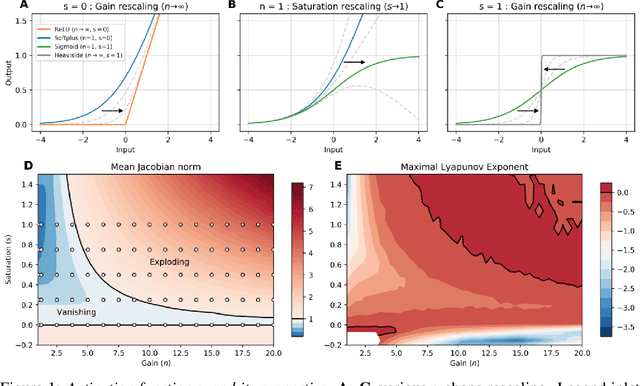
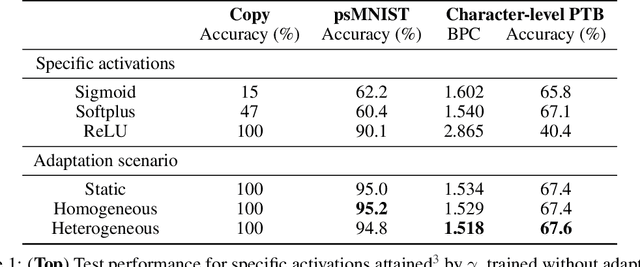
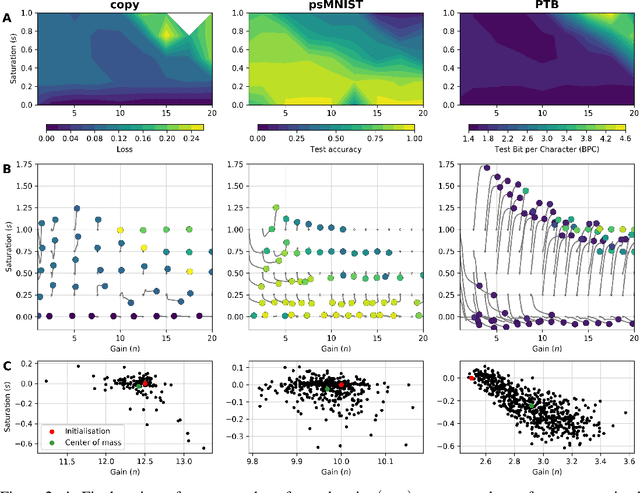
Dynamic adaptation in single-neuron response plays a fundamental role in neural coding in biological neural networks. Yet, most neural activation functions used in artificial networks are fixed and mostly considered as an inconsequential architecture choice. In this paper, we investigate nonlinear activation function adaptation over the large time scale of learning, and outline its impact on sequential processing in recurrent neural networks. We introduce a novel parametric family of nonlinear activation functions, inspired by input-frequency response curves of biological neurons, which allows interpolation between well-known activation functions such as ReLU and sigmoid. Using simple numerical experiments and tools from dynamical systems and information theory, we study the role of neural activation features in learning dynamics. We find that activation adaptation provides distinct task-specific solutions and in some cases, improves both learning speed and performance. Importantly, we find that optimal activation features emerging from our parametric family are considerably different from typical functions used in the literature, suggesting that exploiting the gap between these usual configurations can help learning. Finally, we outline situations where neural activation adaptation alone may help mitigate changes in input statistics in a given task, suggesting mechanisms for transfer learning optimization.