On Neural Architecture Inductive Biases for Relational Tasks

Current deep learning approaches have shown good in-distribution generalization performance, but struggle with out-of-distribution generalization. This is especially true in the case of tasks involving abstract relations like recognizing rules in sequences, as we find in many intelligence tests. Recent work has explored how forcing relational representations to remain distinct from sensory representations, as it seems to be the case in the brain, can help artificial systems. Building on this work, we further explore and formalize the advantages afforded by 'partitioned' representations of relations and sensory details, and how this inductive bias can help recompose learned relational structure in newly encountered settings. We introduce a simple architecture based on similarity scores which we name Compositional Relational Network (CoRelNet). Using this model, we investigate a series of inductive biases that ensure abstract relations are learned and represented distinctly from sensory data, and explore their effects on out-of-distribution generalization for a series of relational psychophysics tasks. We find that simple architectural choices can outperform existing models in out-of-distribution generalization. Together, these results show that partitioning relational representations from other information streams may be a simple way to augment existing network architectures' robustness when performing out-of-distribution relational computations.

Continuous-Time Meta-Learning with Forward Mode Differentiation

Drawing inspiration from gradient-based meta-learning methods with infinitely small gradient steps, we introduce Continuous-Time Meta-Learning (COMLN), a meta-learning algorithm where adaptation follows the dynamics of a gradient vector field. Specifically, representations of the inputs are meta-learned such that a task-specific linear classifier is obtained as a solution of an ordinary differential equation (ODE). Treating the learning process as an ODE offers the notable advantage that the length of the trajectory is now continuous, as opposed to a fixed and discrete number of gradient steps. As a consequence, we can optimize the amount of adaptation necessary to solve a new task using stochastic gradient descent, in addition to learning the initial conditions as is standard practice in gradient-based meta-learning. Importantly, in order to compute the exact meta-gradients required for the outer-loop updates, we devise an efficient algorithm based on forward mode differentiation, whose memory requirements do not scale with the length of the learning trajectory, thus allowing longer adaptation in constant memory. We provide analytical guarantees for the stability of COMLN, we show empirically its efficiency in terms of runtime and memory usage, and we illustrate its effectiveness on a range of few-shot image classification problems.

Catastrophic Fisher Explosion: Early Phase Fisher Matrix Impacts Generalization

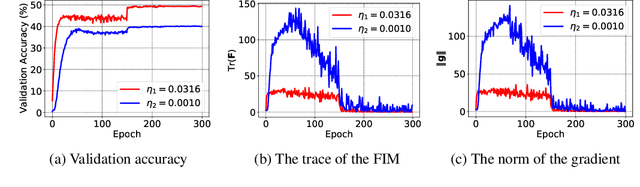
The early phase of training has been shown to be important in two ways for deep neural networks. First, the degree of regularization in this phase significantly impacts the final generalization. Second, it is accompanied by a rapid change in the local loss curvature influenced by regularization choices. Connecting these two findings, we show that stochastic gradient descent (SGD) implicitly penalizes the trace of the Fisher Information Matrix (FIM) from the beginning of training. We argue it is an implicit regularizer in SGD by showing that explicitly penalizing the trace of the FIM can significantly improve generalization. We further show that the early value of the trace of the FIM correlates strongly with the final generalization. We highlight that in the absence of implicit or explicit regularization, the trace of the FIM can increase to a large value early in training, to which we refer as catastrophic Fisher explosion. Finally, to gain insight into the regularization effect of penalizing the trace of the FIM, we show that 1) it limits memorization by reducing the learning speed of examples with noisy labels more than that of the clean examples, and 2) trajectories with a low initial trace of the FIM end in flat minima, which are commonly associated with good generalization.

Advantages of biologically-inspired adaptive neural activation in RNNs during learning

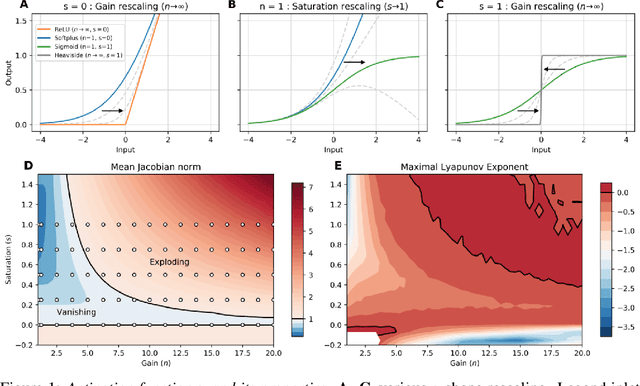
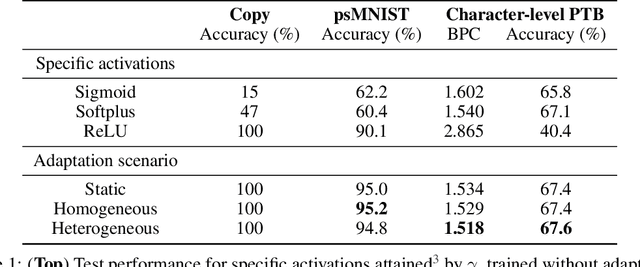
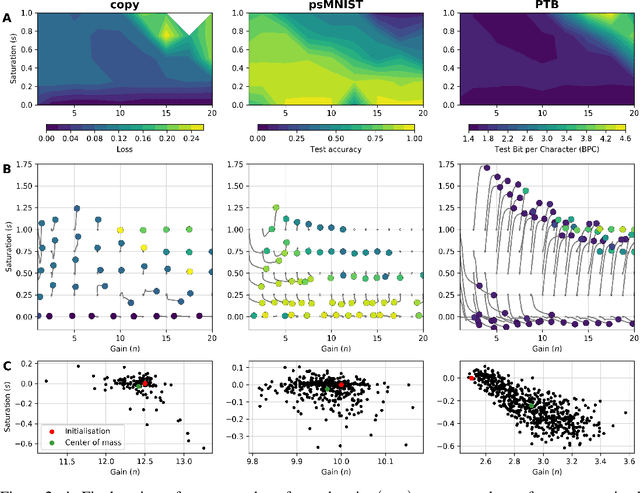
Dynamic adaptation in single-neuron response plays a fundamental role in neural coding in biological neural networks. Yet, most neural activation functions used in artificial networks are fixed and mostly considered as an inconsequential architecture choice. In this paper, we investigate nonlinear activation function adaptation over the large time scale of learning, and outline its impact on sequential processing in recurrent neural networks. We introduce a novel parametric family of nonlinear activation functions, inspired by input-frequency response curves of biological neurons, which allows interpolation between well-known activation functions such as ReLU and sigmoid. Using simple numerical experiments and tools from dynamical systems and information theory, we study the role of neural activation features in learning dynamics. We find that activation adaptation provides distinct task-specific solutions and in some cases, improves both learning speed and performance. Importantly, we find that optimal activation features emerging from our parametric family are considerably different from typical functions used in the literature, suggesting that exploiting the gap between these usual configurations can help learning. Finally, we outline situations where neural activation adaptation alone may help mitigate changes in input statistics in a given task, suggesting mechanisms for transfer learning optimization.

Untangling tradeoffs between recurrence and self-attention in neural networks

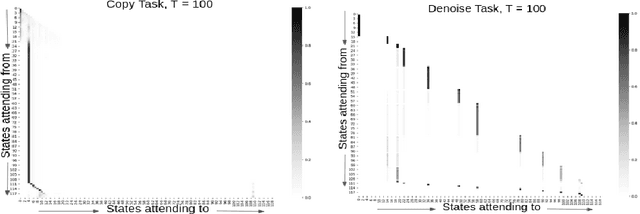
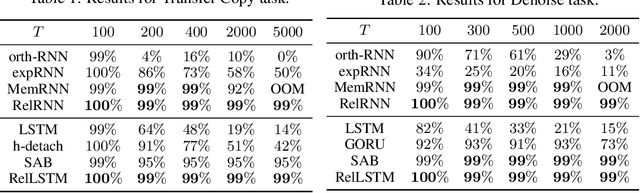
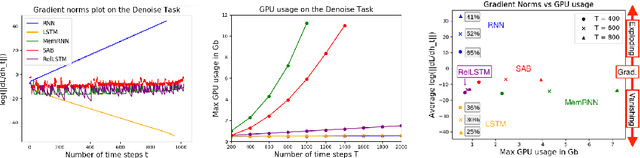
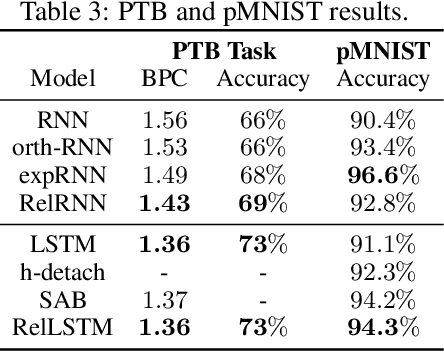
Attention and self-attention mechanisms, inspired by cognitive processes, are now central to state-of-the-art deep learning on sequential tasks. However, most recent progress hinges on heuristic approaches with limited understanding of attention's role in model optimization and computation, and rely on considerable memory and computational resources that scale poorly. In this work, we present a formal analysis of how self-attention affects gradient propagation in recurrent networks, and prove that it mitigates the problem of vanishing gradients when trying to capture long-term dependencies. Building on these results, we propose a relevancy screening mechanism, inspired by the cognitive process of memory consolidation, that allows for a scalable use of sparse self-attention with recurrence. While providing guarantees to avoid vanishing gradients, we use simple numerical experiments to demonstrate the tradeoffs in performance and computational resources by efficiently balancing attention and recurrence. Based on our results, we propose a concrete direction of research to improve scalability of attentive networks.

Non-normal Recurrent Neural Network (nnRNN): learning long time dependencies while improving expressivity with transient dynamics

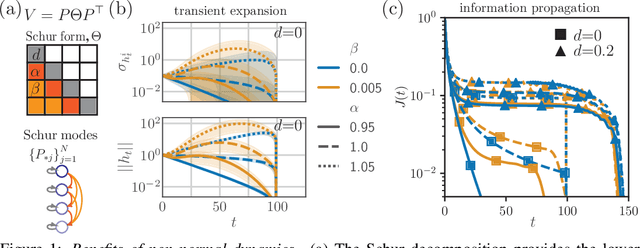
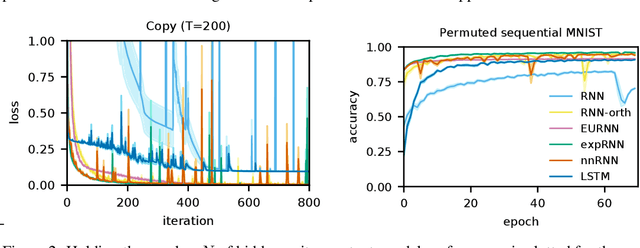
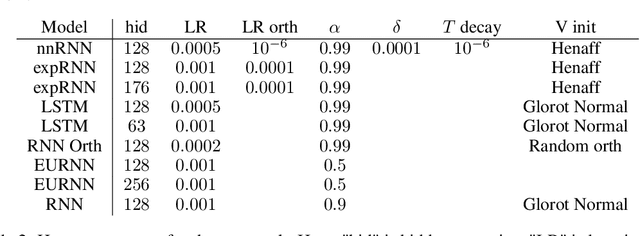
A recent strategy to circumvent the exploding and vanishing gradient problem in RNNs, and to allow the stable propagation of signals over long time scales, is to constrain recurrent connectivity matrices to be orthogonal or unitary. This ensures eigenvalues with unit norm and thus stable dynamics and training. However this comes at the cost of reduced expressivity due to the limited variety of orthogonal transformations. We propose a novel connectivity structure based on the Schur decomposition and a splitting of the Schur form into normal and non-normal parts. This allows to parametrize matrices with unit-norm eigenspectra without orthogonality constraints on eigenbases. The resulting architecture ensures access to a larger space of spectrally constrained matrices, of which orthogonal matrices are a subset. This crucial difference retains the stability advantages and training speed of orthogonal RNNs while enhancing expressivity, especially on tasks that require computations over ongoing input sequences.