Course Correcting Koopman Representations

Koopman representations aim to learn features of nonlinear dynamical systems (NLDS) which lead to linear dynamics in the latent space. Theoretically, such features can be used to simplify many problems in modeling and control of NLDS. In this work we study autoencoder formulations of this problem, and different ways they can be used to model dynamics, specifically for future state prediction over long horizons. We discover several limitations of predicting future states in the latent space and propose an inference-time mechanism, which we refer to as Periodic Reencoding, for faithfully capturing long term dynamics. We justify this method both analytically and empirically via experiments in low and high dimensional NLDS.

Continuous-Time Meta-Learning with Forward Mode Differentiation

Drawing inspiration from gradient-based meta-learning methods with infinitely small gradient steps, we introduce Continuous-Time Meta-Learning (COMLN), a meta-learning algorithm where adaptation follows the dynamics of a gradient vector field. Specifically, representations of the inputs are meta-learned such that a task-specific linear classifier is obtained as a solution of an ordinary differential equation (ODE). Treating the learning process as an ODE offers the notable advantage that the length of the trajectory is now continuous, as opposed to a fixed and discrete number of gradient steps. As a consequence, we can optimize the amount of adaptation necessary to solve a new task using stochastic gradient descent, in addition to learning the initial conditions as is standard practice in gradient-based meta-learning. Importantly, in order to compute the exact meta-gradients required for the outer-loop updates, we devise an efficient algorithm based on forward mode differentiation, whose memory requirements do not scale with the length of the learning trajectory, thus allowing longer adaptation in constant memory. We provide analytical guarantees for the stability of COMLN, we show empirically its efficiency in terms of runtime and memory usage, and we illustrate its effectiveness on a range of few-shot image classification problems.

Simple Video Generation using Neural ODEs

Despite having been studied to a great extent, the task of conditional generation of sequences of frames, or videos, remains extremely challenging. It is a common belief that a key step towards solving this task resides in modelling accurately both spatial and temporal information in video signals. A promising direction to do so has been to learn latent variable models that predict the future in latent space and project back to pixels, as suggested in recent literature. Following this line of work and building on top of a family of models introduced in prior work, Neural ODE, we investigate an approach that models time-continuous dynamics over a continuous latent space with a differential equation with respect to time. The intuition behind this approach is that these trajectories in latent space could then be extrapolated to generate video frames beyond the time steps for which the model is trained. We show that our approach yields promising results in the task of future frame prediction on the Moving MNIST dataset with 1 and 2 digits.

TDprop: Does Jacobi Preconditioning Help Temporal Difference Learning?

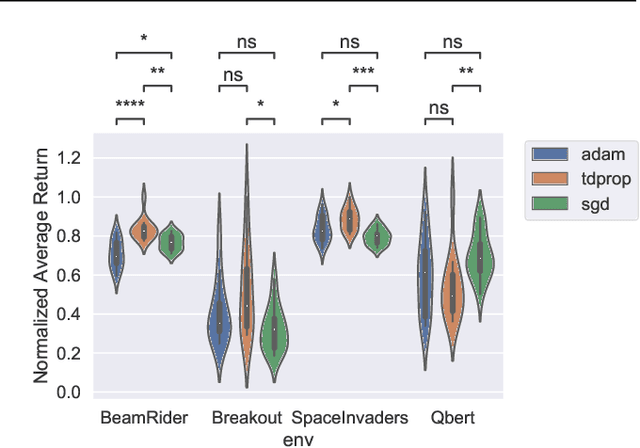
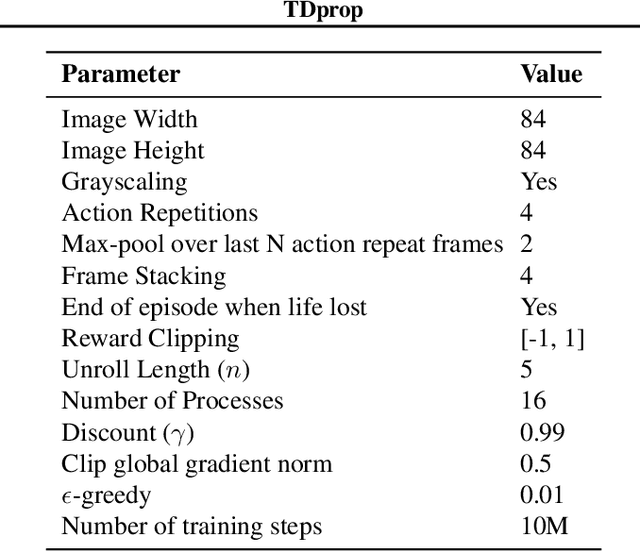
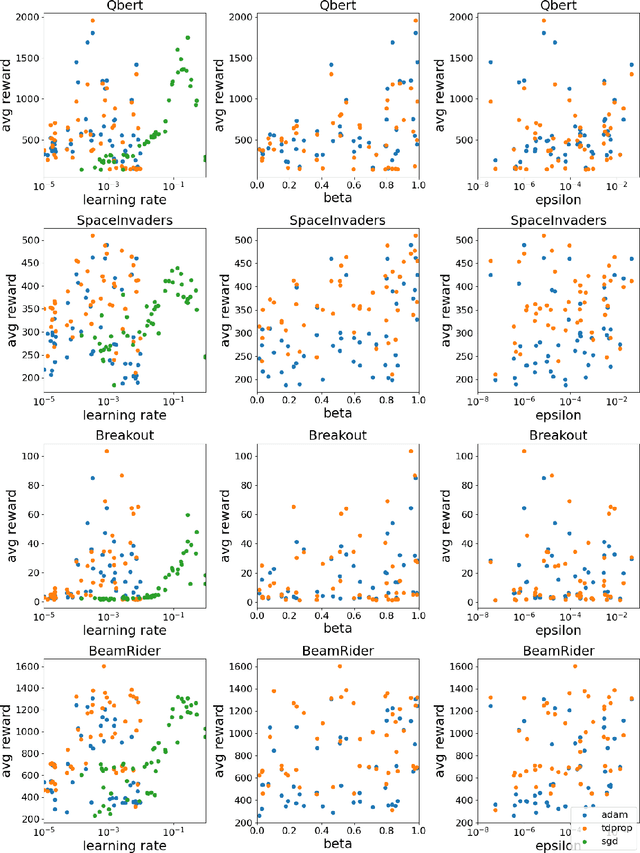
We investigate whether Jacobi preconditioning, accounting for the bootstrap term in temporal difference (TD) learning, can help boost performance of adaptive optimizers. Our method, TDprop, computes a per parameter learning rate based on the diagonal preconditioning of the TD update rule. We show how this can be used in both $n$-step returns and TD($\lambda$). Our theoretical findings demonstrate that including this additional preconditioning information is, surprisingly, comparable to normal semi-gradient TD if the optimal learning rate is found for both via a hyperparameter search. In Deep RL experiments using Expected SARSA, TDprop meets or exceeds the performance of Adam in all tested games under near-optimal learning rates, but a well-tuned SGD can yield similar improvements -- matching our theory. Our findings suggest that Jacobi preconditioning may improve upon typical adaptive optimization methods in Deep RL, but despite incorporating additional information from the TD bootstrap term, may not always be better than SGD.

Recurrent Semi-supervised Classification and Constrained Adversarial Generation with Motion Capture Data

We explore recurrent encoder multi-decoder neural network architectures for semi-supervised sequence classification and reconstruction. We find that the use of multiple reconstruction modules helps models generalize in a classification task when only a small amount of labeled data is available, which is often the case in practice. Such models provide useful high-level representations of motions allowing clustering, searching and faster labeling of new sequences. We also propose a new, realistic partitioning of a well-known, high quality motion-capture dataset for better evaluations. We further explore a novel formulation for future-predicting decoders based on conditional recurrent generative adversarial networks, for which we propose both soft and hard constraints for transition generation derived from desired physical properties of synthesized future movements and desired animation goals. We find that using such constraints allow to stabilize the training of recurrent adversarial architectures for animation generation.