Catastrophic Fisher Explosion: Early Phase Fisher Matrix Impacts Generalization
Paper and Code
Dec 28, 2020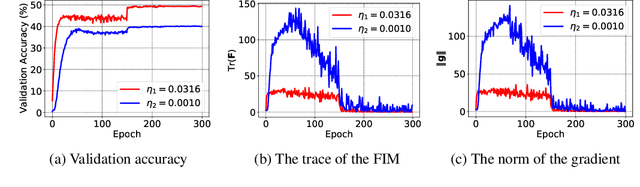



The early phase of training has been shown to be important in two ways for deep neural networks. First, the degree of regularization in this phase significantly impacts the final generalization. Second, it is accompanied by a rapid change in the local loss curvature influenced by regularization choices. Connecting these two findings, we show that stochastic gradient descent (SGD) implicitly penalizes the trace of the Fisher Information Matrix (FIM) from the beginning of training. We argue it is an implicit regularizer in SGD by showing that explicitly penalizing the trace of the FIM can significantly improve generalization. We further show that the early value of the trace of the FIM correlates strongly with the final generalization. We highlight that in the absence of implicit or explicit regularization, the trace of the FIM can increase to a large value early in training, to which we refer as catastrophic Fisher explosion. Finally, to gain insight into the regularization effect of penalizing the trace of the FIM, we show that 1) it limits memorization by reducing the learning speed of examples with noisy labels more than that of the clean examples, and 2) trajectories with a low initial trace of the FIM end in flat minima, which are commonly associated with good generalization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge