A Simulation System Towards Solving Societal-Scale Manipulation

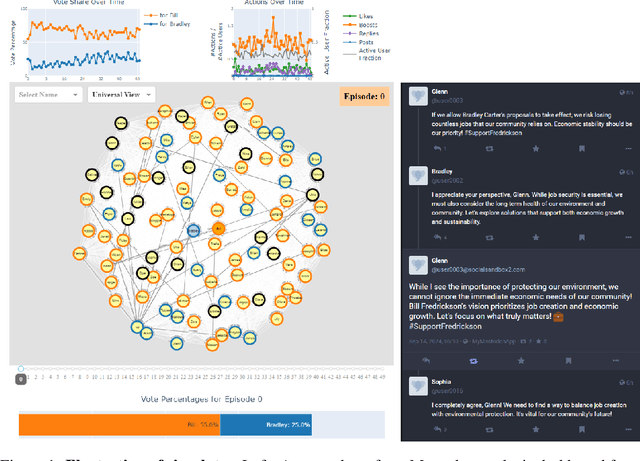
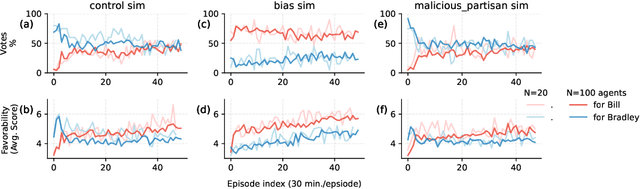
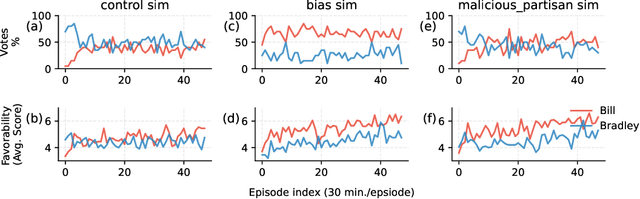
The rise of AI-driven manipulation poses significant risks to societal trust and democratic processes. Yet, studying these effects in real-world settings at scale is ethically and logistically impractical, highlighting a need for simulation tools that can model these dynamics in controlled settings to enable experimentation with possible defenses. We present a simulation environment designed to address this. We elaborate upon the Concordia framework that simulates offline, `real life' activity by adding online interactions to the simulation through social media with the integration of a Mastodon server. We improve simulation efficiency and information flow, and add a set of measurement tools, particularly longitudinal surveys. We demonstrate the simulator with a tailored example in which we track agents' political positions and show how partisan manipulation of agents can affect election results.

Continual Learning In Environments With Polynomial Mixing Times

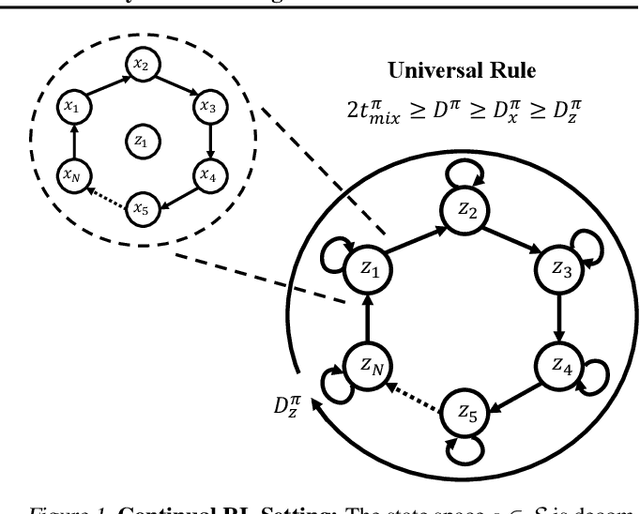
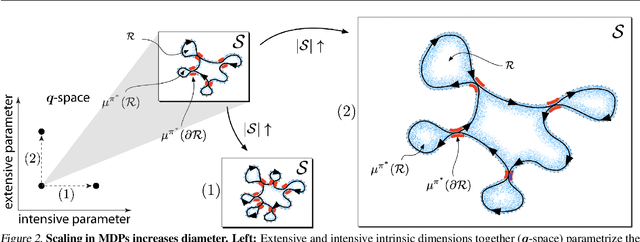
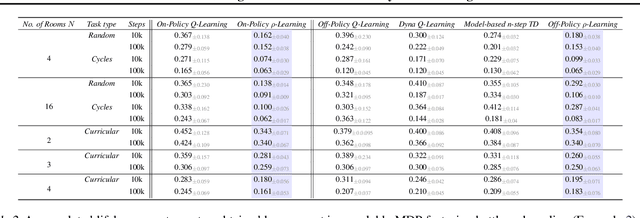
The mixing time of the Markov chain induced by a policy limits performance in real-world continual learning scenarios. Yet, the effect of mixing times on learning in continual reinforcement learning (RL) remains underexplored. In this paper, we characterize problems that are of long-term interest to the development of continual RL, which we call scalable MDPs, through the lens of mixing times. In particular, we establish that scalable MDPs have mixing times that scale polynomially with the size of the problem. We go on to demonstrate that polynomial mixing times present significant difficulties for existing approaches and propose a family of model-based algorithms that speed up learning by directly optimizing for the average reward through a novel bootstrapping procedure. Finally, we perform empirical regret analysis of our proposed approaches, demonstrating clear improvements over baselines and also how scalable MDPs can be used for analysis of RL algorithms as mixing times scale.

On Lyapunov Exponents for RNNs: Understanding Information Propagation Using Dynamical Systems Tools

Recurrent neural networks (RNNs) have been successfully applied to a variety of problems involving sequential data, but their optimization is sensitive to parameter initialization, architecture, and optimizer hyperparameters. Considering RNNs as dynamical systems, a natural way to capture stability, i.e., the growth and decay over long iterates, are the Lyapunov Exponents (LEs), which form the Lyapunov spectrum. The LEs have a bearing on stability of RNN training dynamics because forward propagation of information is related to the backward propagation of error gradients. LEs measure the asymptotic rates of expansion and contraction of nonlinear system trajectories, and generalize stability analysis to the time-varying attractors structuring the non-autonomous dynamics of data-driven RNNs. As a tool to understand and exploit stability of training dynamics, the Lyapunov spectrum fills an existing gap between prescriptive mathematical approaches of limited scope and computationally-expensive empirical approaches. To leverage this tool, we implement an efficient way to compute LEs for RNNs during training, discuss the aspects specific to standard RNN architectures driven by typical sequential datasets, and show that the Lyapunov spectrum can serve as a robust readout of training stability across hyperparameters. With this exposition-oriented contribution, we hope to draw attention to this understudied, but theoretically grounded tool for understanding training stability in RNNs.

Non-normal Recurrent Neural Network (nnRNN): learning long time dependencies while improving expressivity with transient dynamics

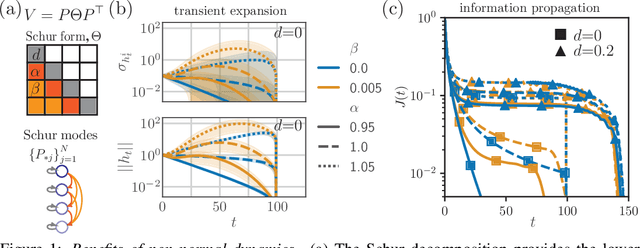
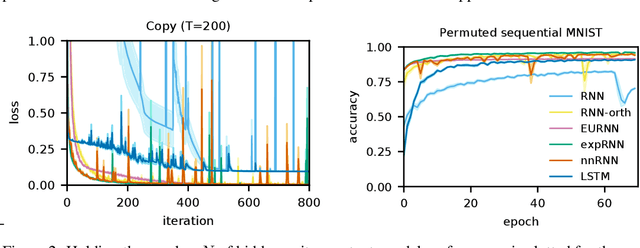
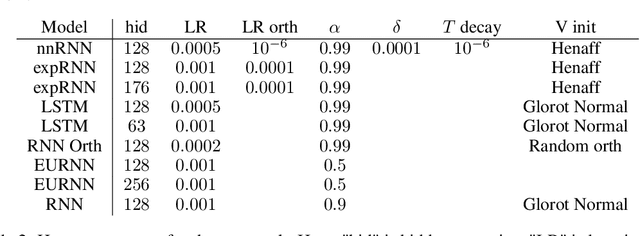
A recent strategy to circumvent the exploding and vanishing gradient problem in RNNs, and to allow the stable propagation of signals over long time scales, is to constrain recurrent connectivity matrices to be orthogonal or unitary. This ensures eigenvalues with unit norm and thus stable dynamics and training. However this comes at the cost of reduced expressivity due to the limited variety of orthogonal transformations. We propose a novel connectivity structure based on the Schur decomposition and a splitting of the Schur form into normal and non-normal parts. This allows to parametrize matrices with unit-norm eigenspectra without orthogonality constraints on eigenbases. The resulting architecture ensures access to a larger space of spectrally constrained matrices, of which orthogonal matrices are a subset. This crucial difference retains the stability advantages and training speed of orthogonal RNNs while enhancing expressivity, especially on tasks that require computations over ongoing input sequences.