Untangling tradeoffs between recurrence and self-attention in neural networks

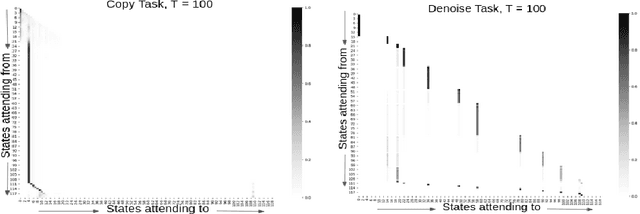
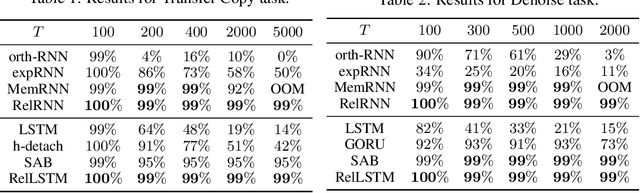
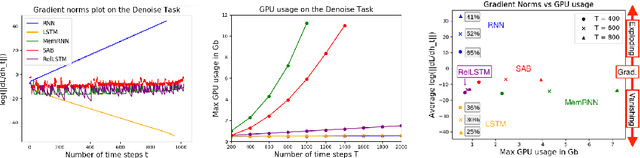
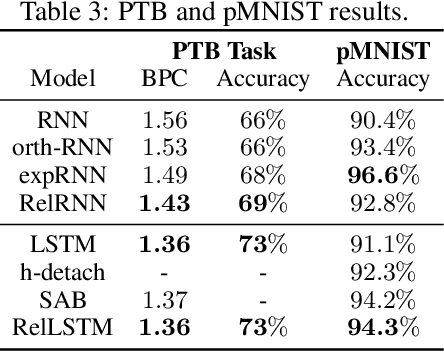
Attention and self-attention mechanisms, inspired by cognitive processes, are now central to state-of-the-art deep learning on sequential tasks. However, most recent progress hinges on heuristic approaches with limited understanding of attention's role in model optimization and computation, and rely on considerable memory and computational resources that scale poorly. In this work, we present a formal analysis of how self-attention affects gradient propagation in recurrent networks, and prove that it mitigates the problem of vanishing gradients when trying to capture long-term dependencies. Building on these results, we propose a relevancy screening mechanism, inspired by the cognitive process of memory consolidation, that allows for a scalable use of sparse self-attention with recurrence. While providing guarantees to avoid vanishing gradients, we use simple numerical experiments to demonstrate the tradeoffs in performance and computational resources by efficiently balancing attention and recurrence. Based on our results, we propose a concrete direction of research to improve scalability of attentive networks.

Non-normal Recurrent Neural Network (nnRNN): learning long time dependencies while improving expressivity with transient dynamics

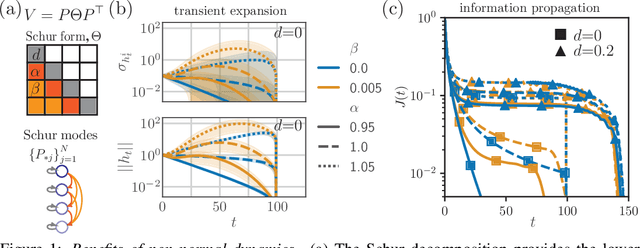
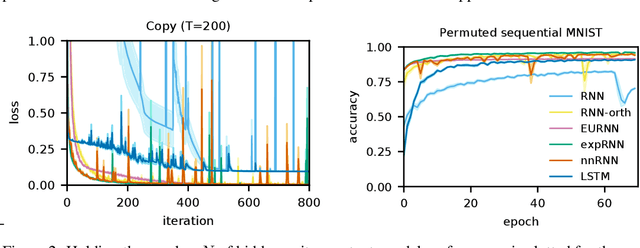
A recent strategy to circumvent the exploding and vanishing gradient problem in RNNs, and to allow the stable propagation of signals over long time scales, is to constrain recurrent connectivity matrices to be orthogonal or unitary. This ensures eigenvalues with unit norm and thus stable dynamics and training. However this comes at the cost of reduced expressivity due to the limited variety of orthogonal transformations. We propose a novel connectivity structure based on the Schur decomposition and a splitting of the Schur form into normal and non-normal parts. This allows to parametrize matrices with unit-norm eigenspectra without orthogonality constraints on eigenbases. The resulting architecture ensures access to a larger space of spectrally constrained matrices, of which orthogonal matrices are a subset. This crucial difference retains the stability advantages and training speed of orthogonal RNNs while enhancing expressivity, especially on tasks that require computations over ongoing input sequences.

Deep Pepper: Expert Iteration based Chess agent in the Reinforcement Learning Setting

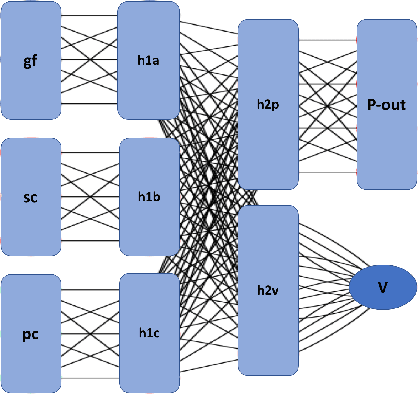
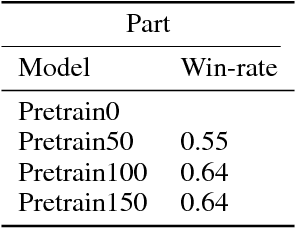
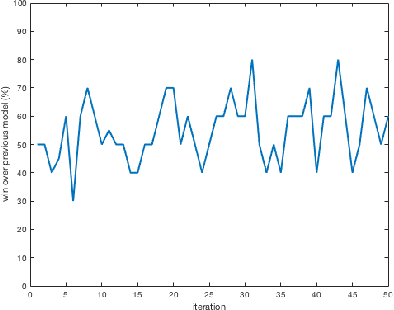
An almost-perfect chess playing agent has been a long standing challenge in the field of Artificial Intelligence. Some of the recent advances demonstrate we are approaching that goal. In this project, we provide methods for faster training of self-play style algorithms, mathematical details of the algorithm used, various potential future directions, and discuss most of the relevant work in the area of computer chess. Deep Pepper uses embedded knowledge to accelerate the training of the chess engine over a "tabula rasa" system such as Alpha Zero. We also release our code to promote further research.