Advantages of biologically-inspired adaptive neural activation in RNNs during learning
Paper and Code
Jun 22, 2020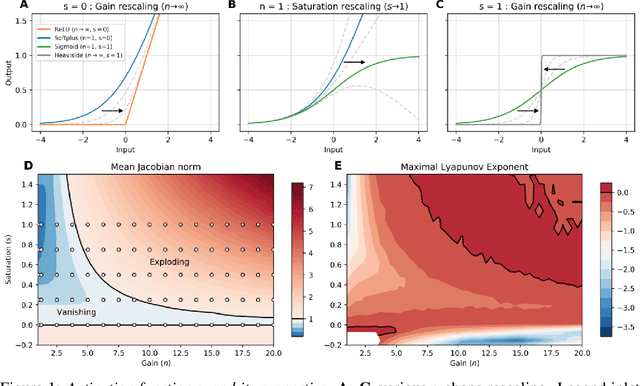
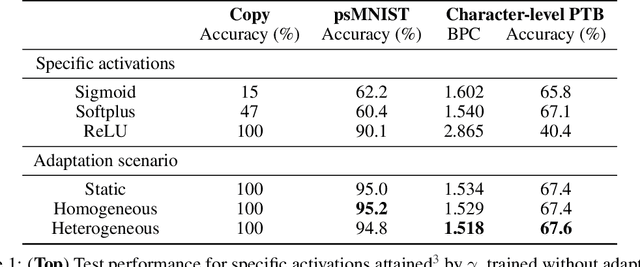
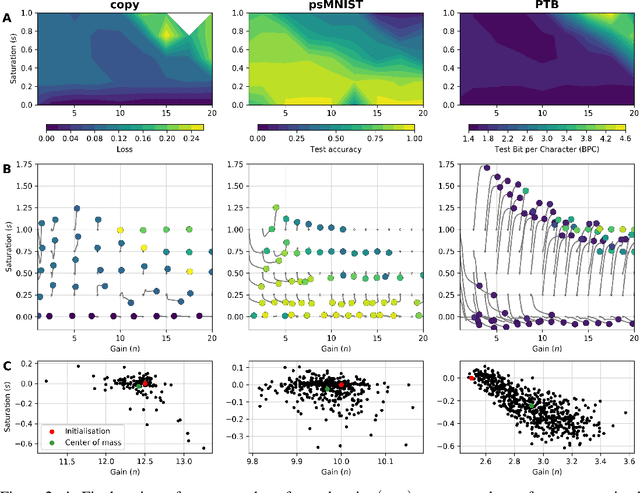

Dynamic adaptation in single-neuron response plays a fundamental role in neural coding in biological neural networks. Yet, most neural activation functions used in artificial networks are fixed and mostly considered as an inconsequential architecture choice. In this paper, we investigate nonlinear activation function adaptation over the large time scale of learning, and outline its impact on sequential processing in recurrent neural networks. We introduce a novel parametric family of nonlinear activation functions, inspired by input-frequency response curves of biological neurons, which allows interpolation between well-known activation functions such as ReLU and sigmoid. Using simple numerical experiments and tools from dynamical systems and information theory, we study the role of neural activation features in learning dynamics. We find that activation adaptation provides distinct task-specific solutions and in some cases, improves both learning speed and performance. Importantly, we find that optimal activation features emerging from our parametric family are considerably different from typical functions used in the literature, suggesting that exploiting the gap between these usual configurations can help learning. Finally, we outline situations where neural activation adaptation alone may help mitigate changes in input statistics in a given task, suggesting mechanisms for transfer learning optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge