Unlocking the Potential of Similarity Matching: Scalability, Supervision and Pre-training

While effective, the backpropagation (BP) algorithm exhibits limitations in terms of biological plausibility, computational cost, and suitability for online learning. As a result, there has been a growing interest in developing alternative biologically plausible learning approaches that rely on local learning rules. This study focuses on the primarily unsupervised similarity matching (SM) framework, which aligns with observed mechanisms in biological systems and offers online, localized, and biologically plausible algorithms. i) To scale SM to large datasets, we propose an implementation of Convolutional Nonnegative SM using PyTorch. ii) We introduce a localized supervised SM objective reminiscent of canonical correlation analysis, facilitating stacking SM layers. iii) We leverage the PyTorch implementation for pre-training architectures such as LeNet and compare the evaluation of features against BP-trained models. This work combines biologically plausible algorithms with computational efficiency opening multiple avenues for further explorations.

A normative framework for deriving neural networks with multi-compartmental neurons and non-Hebbian plasticity

An established normative approach for understanding the algorithmic basis of neural computation is to derive online algorithms from principled computational objectives and evaluate their compatibility with anatomical and physiological observations. Similarity matching objectives have served as successful starting points for deriving online algorithms that map onto neural networks (NNs) with point neurons and Hebbian/anti-Hebbian plasticity. These NN models account for many anatomical and physiological observations; however, the objectives have limited computational power and the derived NNs do not explain multi-compartmental neuronal structures and non-Hebbian forms of plasticity that are prevalent throughout the brain. In this article, we review and unify recent extensions of the similarity matching approach to address more complex objectives, including a broad range of unsupervised and self-supervised learning tasks that can be formulated as generalized eigenvalue problems or nonnegative matrix factorization problems. Interestingly, the online algorithms derived from these objectives naturally map onto NNs with multi-compartmental neurons and local, non-Hebbian learning rules. Therefore, this unified extension of the similarity matching approach provides a normative framework that facilitates understanding the multi-compartmental neuronal structures and non-Hebbian plasticity found throughout the brain.

Neural optimal feedback control with local learning rules

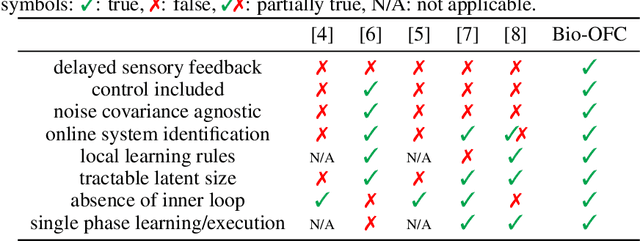
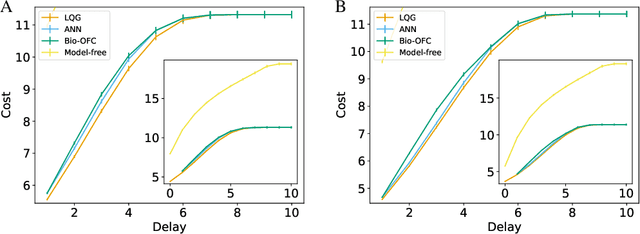
A major problem in motor control is understanding how the brain plans and executes proper movements in the face of delayed and noisy stimuli. A prominent framework for addressing such control problems is Optimal Feedback Control (OFC). OFC generates control actions that optimize behaviorally relevant criteria by integrating noisy sensory stimuli and the predictions of an internal model using the Kalman filter or its extensions. However, a satisfactory neural model of Kalman filtering and control is lacking because existing proposals have the following limitations: not considering the delay of sensory feedback, training in alternating phases, and requiring knowledge of the noise covariance matrices, as well as that of systems dynamics. Moreover, the majority of these studies considered Kalman filtering in isolation, and not jointly with control. To address these shortcomings, we introduce a novel online algorithm which combines adaptive Kalman filtering with a model free control approach (i.e., policy gradient algorithm). We implement this algorithm in a biologically plausible neural network with local synaptic plasticity rules. This network performs system identification and Kalman filtering, without the need for multiple phases with distinct update rules or the knowledge of the noise covariances. It can perform state estimation with delayed sensory feedback, with the help of an internal model. It learns the control policy without requiring any knowledge of the dynamics, thus avoiding the need for weight transport. In this way, our implementation of OFC solves the credit assignment problem needed to produce the appropriate sensory-motor control in the presence of stimulus delay.

A Similarity-preserving Neural Network Trained on Transformed Images Recapitulates Salient Features of the Fly Motion Detection Circuit

Learning to detect content-independent transformations from data is one of the central problems in biological and artificial intelligence. An example of such problem is unsupervised learning of a visual motion detector from pairs of consecutive video frames. Rao and Ruderman formulated this problem in terms of learning infinitesimal transformation operators (Lie group generators) via minimizing image reconstruction error. Unfortunately, it is difficult to map their model onto a biologically plausible neural network (NN) with local learning rules. Here we propose a biologically plausible model of motion detection. We also adopt the transformation-operator approach but, instead of reconstruction-error minimization, start with a similarity-preserving objective function. An online algorithm that optimizes such an objective function naturally maps onto an NN with biologically plausible learning rules. The trained NN recapitulates major features of the well-studied motion detector in the fly. In particular, it is consistent with the experimental observation that local motion detectors combine information from at least three adjacent pixels, something that contradicts the celebrated Hassenstein-Reichardt model.

A biologically plausible neural network for local supervision in cortical microcircuits

The backpropagation algorithm is an invaluable tool for training artificial neural networks; however, because of a weight sharing requirement, it does not provide a plausible model of brain function. Here, in the context of a two-layer network, we derive an algorithm for training a neural network which avoids this problem by not requiring explicit error computation and backpropagation. Furthermore, our algorithm maps onto a neural network that bears a remarkable resemblance to the connectivity structure and learning rules of the cortex. We find that our algorithm empirically performs comparably to backprop on a number of datasets.

A simple normative network approximates local non-Hebbian learning in the cortex

To guide behavior, the brain extracts relevant features from high-dimensional data streamed by sensory organs. Neuroscience experiments demonstrate that the processing of sensory inputs by cortical neurons is modulated by instructive signals which provide context and task-relevant information. Here, adopting a normative approach, we model these instructive signals as supervisory inputs guiding the projection of the feedforward data. Mathematically, we start with a family of Reduced-Rank Regression (RRR) objective functions which include Reduced Rank (minimum) Mean Square Error (RRMSE) and Canonical Correlation Analysis (CCA), and derive novel offline and online optimization algorithms, which we call Bio-RRR. The online algorithms can be implemented by neural networks whose synaptic learning rules resemble calcium plateau potential dependent plasticity observed in the cortex. We detail how, in our model, the calcium plateau potential can be interpreted as a backpropagating error signal. We demonstrate that, despite relying exclusively on biologically plausible local learning rules, our algorithms perform competitively with existing implementations of RRMSE and CCA.

A biologically plausible neural network for multi-channel Canonical Correlation Analysis

Cortical pyramidal neurons receive inputs from multiple distinct neural populations and integrate these inputs in separate dendritic compartments. We explore the possibility that cortical microcircuits implement Canonical Correlation Analysis (CCA), an unsupervised learning method that projects the inputs onto a common subspace so as to maximize the correlations between the projections. To this end, we seek a multi-channel CCA algorithm that can be implemented in a biologically plausible neural network. For biological plausibility, we require that the network operates in the online setting and its synaptic update rules are local. Starting from a novel CCA objective function, we derive an online optimization algorithm whose optimization steps can be implemented in a single-layer neural network with multi-compartmental neurons and local non-Hebbian learning rules. We also derive an extension of our online CCA algorithm with adaptive output rank and output whitening. Interestingly, the extension maps onto a neural network whose neural architecture and synaptic updates resemble neural circuitry and synaptic plasticity observed experimentally in cortical pyramidal neurons.

A Neural Network for Semi-Supervised Learning on Manifolds

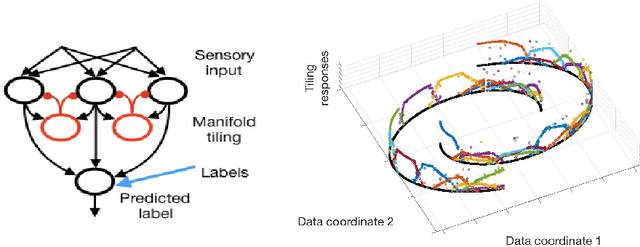
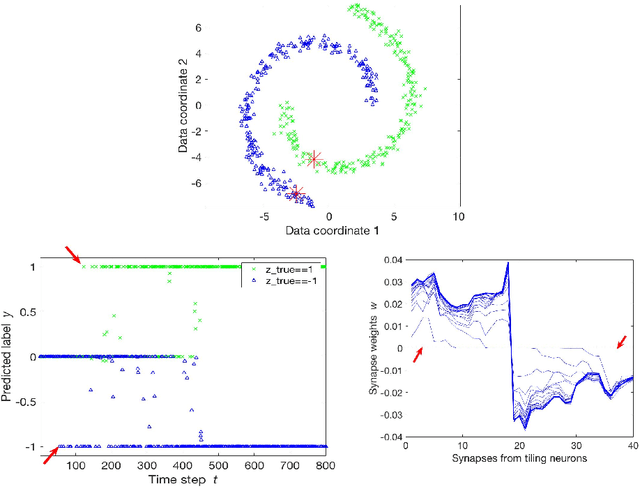
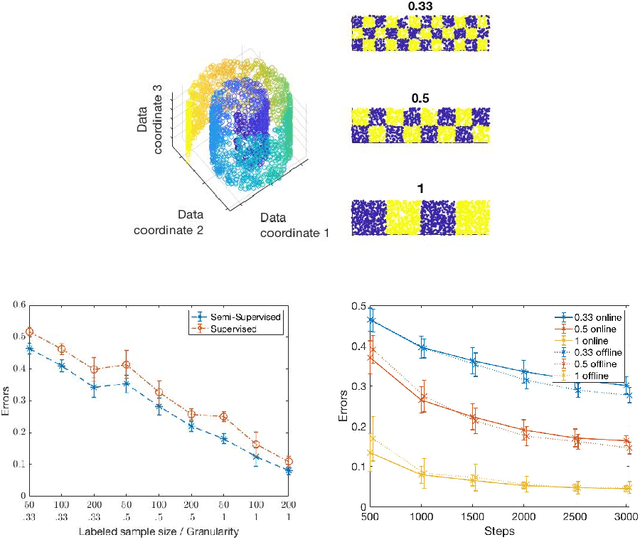
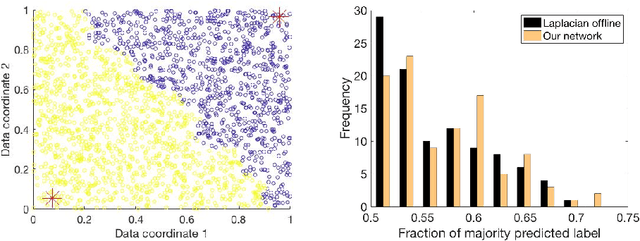
Semi-supervised learning algorithms typically construct a weighted graph of data points to represent a manifold. However, an explicit graph representation is problematic for neural networks operating in the online setting. Here, we propose a feed-forward neural network capable of semi-supervised learning on manifolds without using an explicit graph representation. Our algorithm uses channels that represent localities on the manifold such that correlations between channels represent manifold structure. The proposed neural network has two layers. The first layer learns to build a representation of low-dimensional manifolds in the input data as proposed recently in [8]. The second learns to classify data using both occasional supervision and similarity of the manifold representation of the data. The channel carrying label information for the second layer is assumed to be "silent" most of the time. Learning in both layers is Hebbian, making our network design biologically plausible. We experimentally demonstrate the effect of semi-supervised learning on non-trivial manifolds.

Clustering is semidefinitely not that hard: Nonnegative SDP for manifold disentangling

In solving hard computational problems, semidefinite program (SDP) relaxations often play an important role because they come with a guarantee of optimality. Here, we focus on a popular semidefinite relaxation of K-means clustering which yields the same solution as the non-convex original formulation for well segregated datasets. We report an unexpected finding: when data contains (greater than zero-dimensional) manifolds, the SDP solution captures such geometrical structures. Unlike traditional manifold embedding techniques, our approach does not rely on manually defining a kernel but rather enforces locality via a nonnegativity constraint. We thus call our approach NOnnegative MAnifold Disentangling, or NOMAD. To build an intuitive understanding of its manifold learning capabilities, we develop a theoretical analysis of NOMAD on idealized datasets. While NOMAD is convex and the globally optimal solution can be found by generic SDP solvers with polynomial time complexity, they are too slow for modern datasets. To address this problem, we analyze a non-convex heuristic and present a new, convex and yet efficient, algorithm, based on the conditional gradient method. Our results render NOMAD a versatile, understandable, and powerful tool for manifold learning.