An Out-of-Domain Synapse Detection Challenge for Microwasp Brain Connectomes

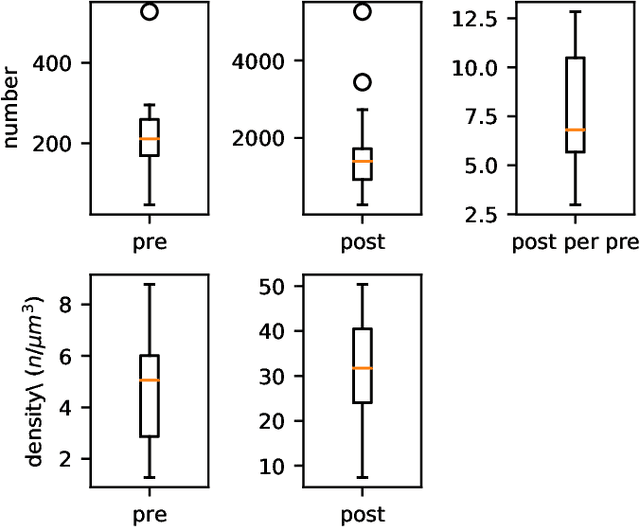
The size of image stacks in connectomics studies now reaches the terabyte and often petabyte scales with a great diversity of appearance across brain regions and samples. However, manual annotation of neural structures, e.g., synapses, is time-consuming, which leads to limited training data often smaller than 0.001\% of the test data in size. Domain adaptation and generalization approaches were proposed to address similar issues for natural images, which were less evaluated on connectomics data due to a lack of out-of-domain benchmarks.

Toward Next-Generation Artificial Intelligence: Catalyzing the NeuroAI Revolution

Neuroscience has long been an important driver of progress in artificial intelligence (AI). We propose that to accelerate progress in AI, we must invest in fundamental research in NeuroAI.

A Neural Network for Semi-Supervised Learning on Manifolds

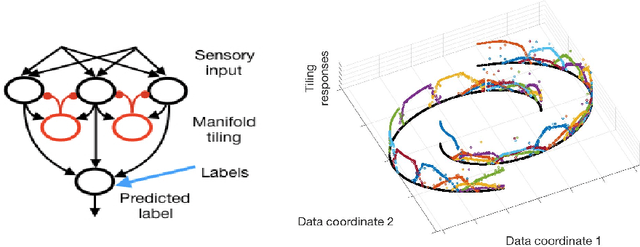
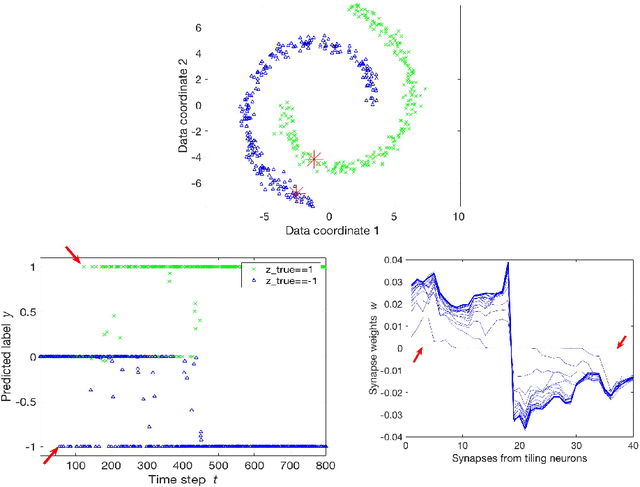
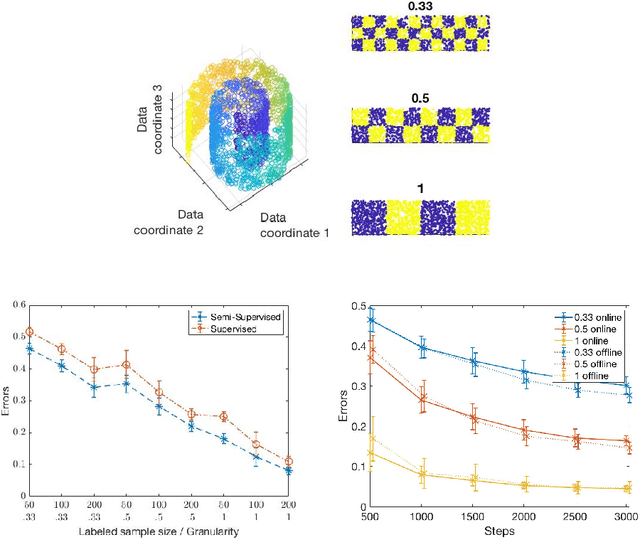
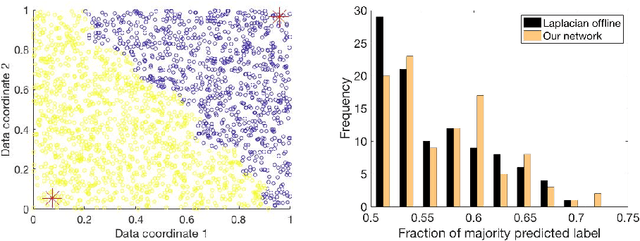
Semi-supervised learning algorithms typically construct a weighted graph of data points to represent a manifold. However, an explicit graph representation is problematic for neural networks operating in the online setting. Here, we propose a feed-forward neural network capable of semi-supervised learning on manifolds without using an explicit graph representation. Our algorithm uses channels that represent localities on the manifold such that correlations between channels represent manifold structure. The proposed neural network has two layers. The first layer learns to build a representation of low-dimensional manifolds in the input data as proposed recently in [8]. The second learns to classify data using both occasional supervision and similarity of the manifold representation of the data. The channel carrying label information for the second layer is assumed to be "silent" most of the time. Learning in both layers is Hebbian, making our network design biologically plausible. We experimentally demonstrate the effect of semi-supervised learning on non-trivial manifolds.

Clustering is semidefinitely not that hard: Nonnegative SDP for manifold disentangling

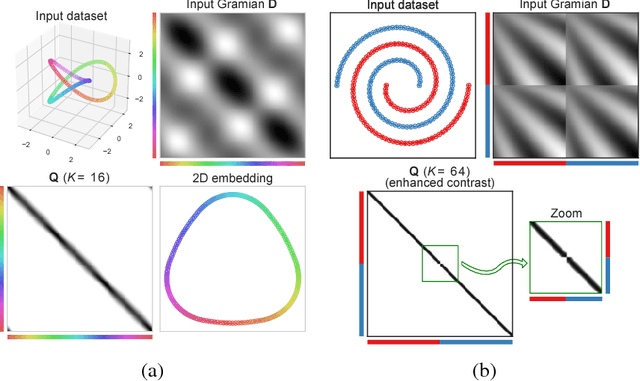
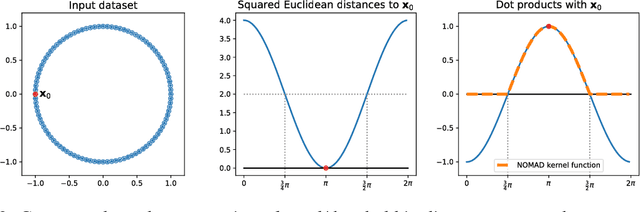
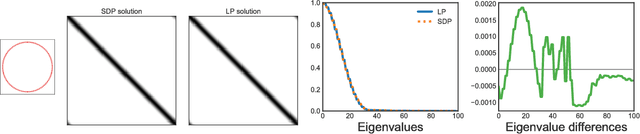
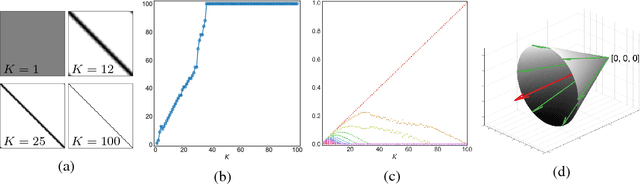
In solving hard computational problems, semidefinite program (SDP) relaxations often play an important role because they come with a guarantee of optimality. Here, we focus on a popular semidefinite relaxation of K-means clustering which yields the same solution as the non-convex original formulation for well segregated datasets. We report an unexpected finding: when data contains (greater than zero-dimensional) manifolds, the SDP solution captures such geometrical structures. Unlike traditional manifold embedding techniques, our approach does not rely on manually defining a kernel but rather enforces locality via a nonnegativity constraint. We thus call our approach NOnnegative MAnifold Disentangling, or NOMAD. To build an intuitive understanding of its manifold learning capabilities, we develop a theoretical analysis of NOMAD on idealized datasets. While NOMAD is convex and the globally optimal solution can be found by generic SDP solvers with polynomial time complexity, they are too slow for modern datasets. To address this problem, we analyze a non-convex heuristic and present a new, convex and yet efficient, algorithm, based on the conditional gradient method. Our results render NOMAD a versatile, understandable, and powerful tool for manifold learning.

Super-resolution using Sparse Representations over Learned Dictionaries: Reconstruction of Brain Structure using Electron Microscopy

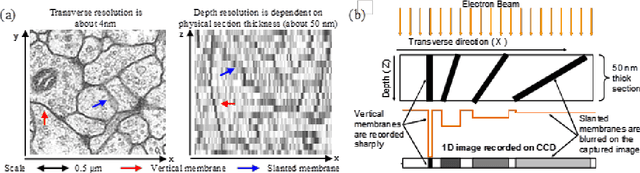
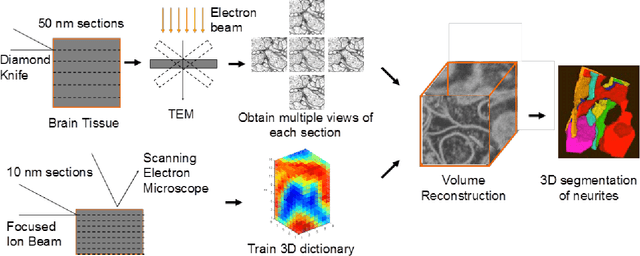
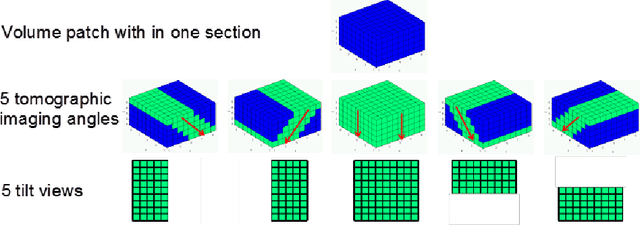
A central problem in neuroscience is reconstructing neuronal circuits on the synapse level. Due to a wide range of scales in brain architecture such reconstruction requires imaging that is both high-resolution and high-throughput. Existing electron microscopy (EM) techniques possess required resolution in the lateral plane and either high-throughput or high depth resolution but not both. Here, we exploit recent advances in unsupervised learning and signal processing to obtain high depth-resolution EM images computationally without sacrificing throughput. First, we show that the brain tissue can be represented as a sparse linear combination of localized basis functions that are learned using high-resolution datasets. We then develop compressive sensing-inspired techniques that can reconstruct the brain tissue from very few (typically 5) tomographic views of each section. This enables tracing of neuronal processes and, hence, high throughput reconstruction of neural circuits on the level of individual synapses.