The Neuron as a Direct Data-Driven Controller

In the quest to model neuronal function amidst gaps in physiological data, a promising strategy is to develop a normative theory that interprets neuronal physiology as optimizing a computational objective. This study extends the current normative models, which primarily optimize prediction, by conceptualizing neurons as optimal feedback controllers. We posit that neurons, especially those beyond early sensory areas, act as controllers, steering their environment towards a specific desired state through their output. This environment comprises both synaptically interlinked neurons and external motor sensory feedback loops, enabling neurons to evaluate the effectiveness of their control via synaptic feedback. Utilizing the novel Direct Data-Driven Control (DD-DC) framework, we model neurons as biologically feasible controllers which implicitly identify loop dynamics, infer latent states and optimize control. Our DD-DC neuron model explains various neurophysiological phenomena: the shift from potentiation to depression in Spike-Timing-Dependent Plasticity (STDP) with its asymmetry, the duration and adaptive nature of feedforward and feedback neuronal filters, the imprecision in spike generation under constant stimulation, and the characteristic operational variability and noise in the brain. Our model presents a significant departure from the traditional, feedforward, instant-response McCulloch-Pitts-Rosenblatt neuron, offering a novel and biologically-informed fundamental unit for constructing neural networks.

Neural optimal feedback control with local learning rules

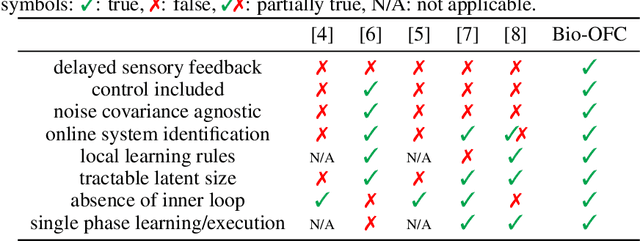
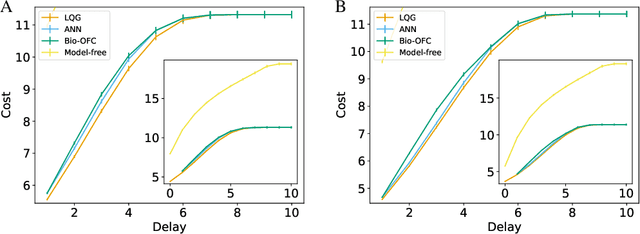
A major problem in motor control is understanding how the brain plans and executes proper movements in the face of delayed and noisy stimuli. A prominent framework for addressing such control problems is Optimal Feedback Control (OFC). OFC generates control actions that optimize behaviorally relevant criteria by integrating noisy sensory stimuli and the predictions of an internal model using the Kalman filter or its extensions. However, a satisfactory neural model of Kalman filtering and control is lacking because existing proposals have the following limitations: not considering the delay of sensory feedback, training in alternating phases, and requiring knowledge of the noise covariance matrices, as well as that of systems dynamics. Moreover, the majority of these studies considered Kalman filtering in isolation, and not jointly with control. To address these shortcomings, we introduce a novel online algorithm which combines adaptive Kalman filtering with a model free control approach (i.e., policy gradient algorithm). We implement this algorithm in a biologically plausible neural network with local synaptic plasticity rules. This network performs system identification and Kalman filtering, without the need for multiple phases with distinct update rules or the knowledge of the noise covariances. It can perform state estimation with delayed sensory feedback, with the help of an internal model. It learns the control policy without requiring any knowledge of the dynamics, thus avoiding the need for weight transport. In this way, our implementation of OFC solves the credit assignment problem needed to produce the appropriate sensory-motor control in the presence of stimulus delay.

A Neural Network for Semi-Supervised Learning on Manifolds

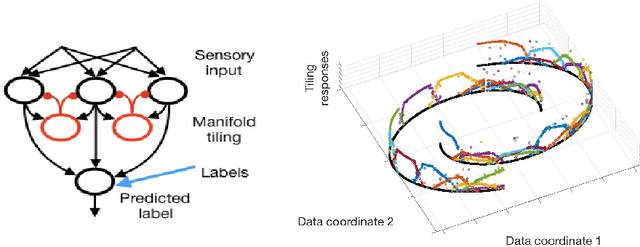
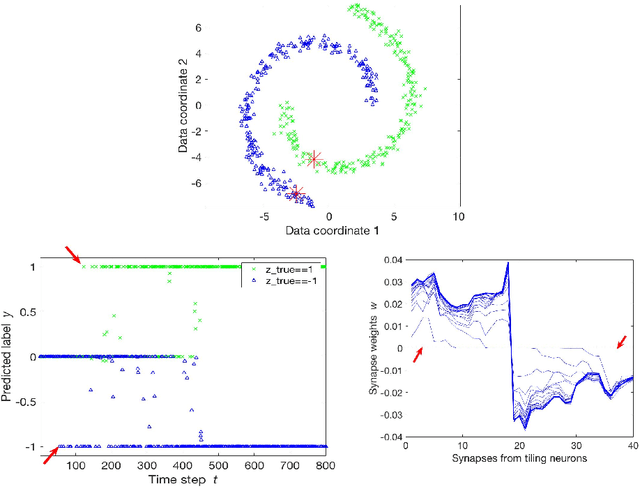
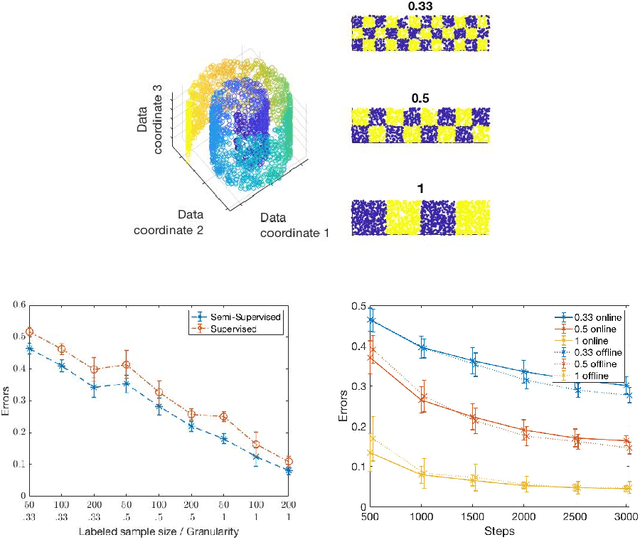
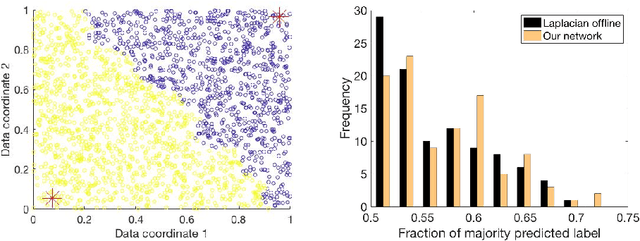
Semi-supervised learning algorithms typically construct a weighted graph of data points to represent a manifold. However, an explicit graph representation is problematic for neural networks operating in the online setting. Here, we propose a feed-forward neural network capable of semi-supervised learning on manifolds without using an explicit graph representation. Our algorithm uses channels that represent localities on the manifold such that correlations between channels represent manifold structure. The proposed neural network has two layers. The first layer learns to build a representation of low-dimensional manifolds in the input data as proposed recently in [8]. The second learns to classify data using both occasional supervision and similarity of the manifold representation of the data. The channel carrying label information for the second layer is assumed to be "silent" most of the time. Learning in both layers is Hebbian, making our network design biologically plausible. We experimentally demonstrate the effect of semi-supervised learning on non-trivial manifolds.

Distributed Coordinate Descent for Generalized Linear Models with Regularization

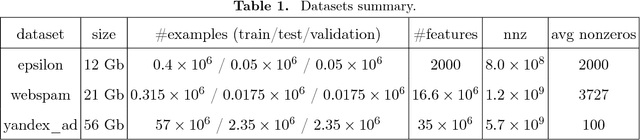
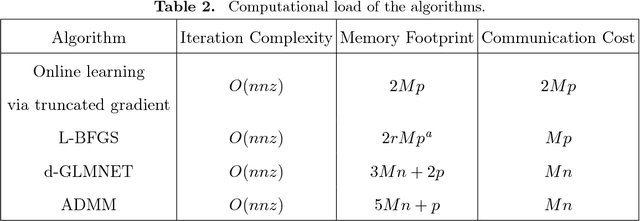
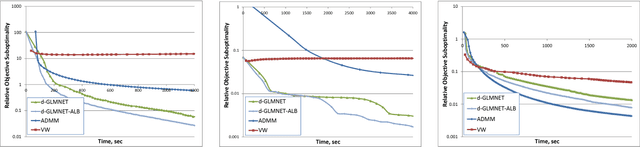
Generalized linear model with $L_1$ and $L_2$ regularization is a widely used technique for solving classification, class probability estimation and regression problems. With the numbers of both features and examples growing rapidly in the fields like text mining and clickstream data analysis parallelization and the use of cluster architectures becomes important. We present a novel algorithm for fitting regularized generalized linear models in the distributed environment. The algorithm splits data between nodes by features, uses coordinate descent on each node and line search to merge results globally. Convergence proof is provided. A modifications of the algorithm addresses slow node problem. For an important particular case of logistic regression we empirically compare our program with several state-of-the art approaches that rely on different algorithmic and data spitting methods. Experiments demonstrate that our approach is scalable and superior when training on large and sparse datasets.

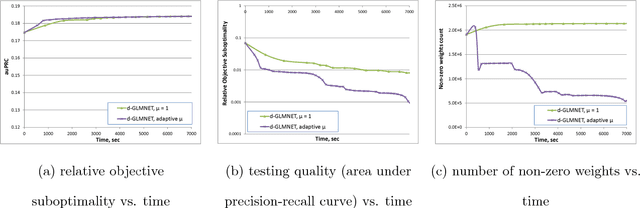
Distributed Coordinate Descent for L1-regularized Logistic Regression

Solving logistic regression with L1-regularization in distributed settings is an important problem. This problem arises when training dataset is very large and cannot fit the memory of a single machine. We present d-GLMNET, a new algorithm solving logistic regression with L1-regularization in the distributed settings. We empirically show that it is superior over distributed online learning via truncated gradient.

A network of spiking neurons for computing sparse representations in an energy efficient way

Computing sparse redundant representations is an important problem both in applied mathematics and neuroscience. In many applications, this problem must be solved in an energy efficient way. Here, we propose a hybrid distributed algorithm (HDA), which solves this problem on a network of simple nodes communicating via low-bandwidth channels. HDA nodes perform both gradient-descent-like steps on analog internal variables and coordinate-descent-like steps via quantized external variables communicated to each other. Interestingly, such operation is equivalent to a network of integrate-and-fire neurons, suggesting that HDA may serve as a model of neural computation. We show that the numerical performance of HDA is on par with existing algorithms. In the asymptotic regime the representation error of HDA decays with time, t, as 1/t. HDA is stable against time-varying noise, specifically, the representation error decays as 1/sqrt(t) for Gaussian white noise.