Distributed Coordinate Descent for Generalized Linear Models with Regularization
Paper and Code
Jun 26, 2017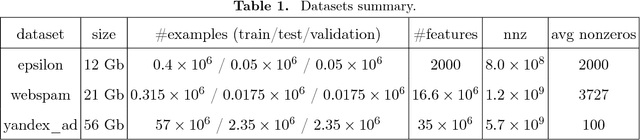
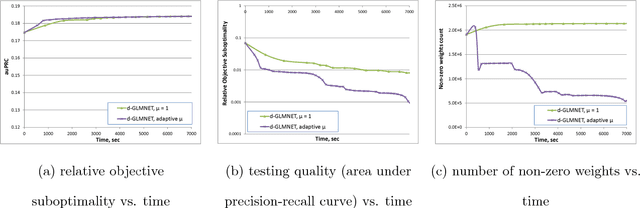
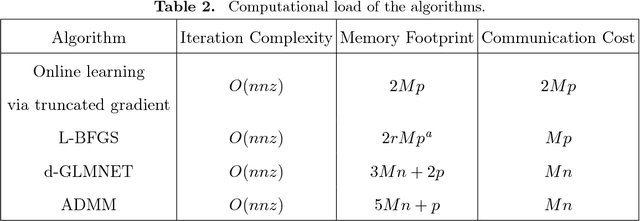
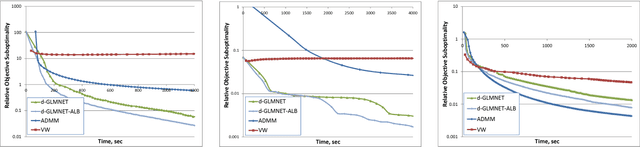
Generalized linear model with $L_1$ and $L_2$ regularization is a widely used technique for solving classification, class probability estimation and regression problems. With the numbers of both features and examples growing rapidly in the fields like text mining and clickstream data analysis parallelization and the use of cluster architectures becomes important. We present a novel algorithm for fitting regularized generalized linear models in the distributed environment. The algorithm splits data between nodes by features, uses coordinate descent on each node and line search to merge results globally. Convergence proof is provided. A modifications of the algorithm addresses slow node problem. For an important particular case of logistic regression we empirically compare our program with several state-of-the art approaches that rely on different algorithmic and data spitting methods. Experiments demonstrate that our approach is scalable and superior when training on large and sparse datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge