ColBERT-serve: Efficient Multi-Stage Memory-Mapped Scoring

We study serving retrieval models, specifically late interaction models like ColBERT, to many concurrent users at once and under a small budget, in which the index may not fit in memory. We present ColBERT-serve, a novel serving system that applies a memory-mapping strategy to the ColBERT index, reducing RAM usage by 90% and permitting its deployment on cheap servers, and incorporates a multi-stage architecture with hybrid scoring, reducing ColBERT's query latency and supporting many concurrent queries in parallel.

Toward Next-Generation Artificial Intelligence: Catalyzing the NeuroAI Revolution

Neuroscience has long been an important driver of progress in artificial intelligence (AI). We propose that to accelerate progress in AI, we must invest in fundamental research in NeuroAI.

Online Learning Without Prior Information

The vast majority of optimization and online learning algorithms today require some prior information about the data (often in the form of bounds on gradients or on the optimal parameter value). When this information is not available, these algorithms require laborious manual tuning of various hyperparameters, motivating the search for algorithms that can adapt to the data with no prior information. We describe a frontier of new lower bounds on the performance of such algorithms, reflecting a tradeoff between a term that depends on the optimal parameter value and a term that depends on the gradients' rate of growth. Further, we construct a family of algorithms whose performance matches any desired point on this frontier, which no previous algorithm reaches.

Online Convex Optimization with Unconstrained Domains and Losses

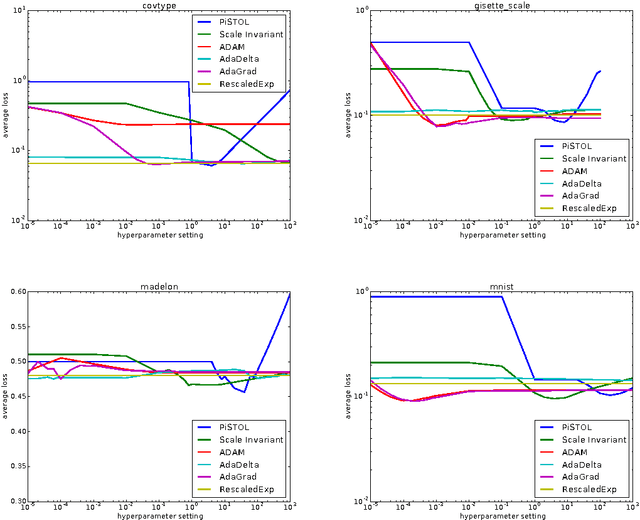
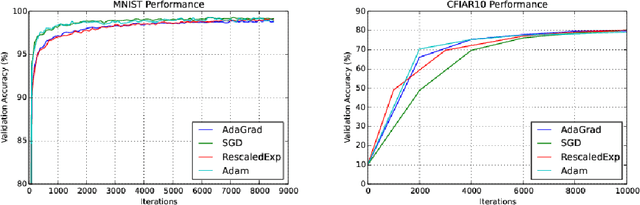
We propose an online convex optimization algorithm (RescaledExp) that achieves optimal regret in the unconstrained setting without prior knowledge of any bounds on the loss functions. We prove a lower bound showing an exponential separation between the regret of existing algorithms that require a known bound on the loss functions and any algorithm that does not require such knowledge. RescaledExp matches this lower bound asymptotically in the number of iterations. RescaledExp is naturally hyperparameter-free and we demonstrate empirically that it matches prior optimization algorithms that require hyperparameter optimization.