The kernel of graph indices for vector search

The most popular graph indices for vector search use principles from computational geometry to build the graph. Hence, their formal graph navigability guarantees are only valid in Euclidean space. In this work, we show that machine learning can be used to build graph indices for vector search in metric and non-metric vector spaces (e.g., for inner product similarity). From this novel perspective, we introduce the Support Vector Graph (SVG), a new type of graph index that leverages kernel methods to establish the graph connectivity and that comes with formal navigability guarantees valid in metric and non-metric vector spaces. In addition, we interpret the most popular graph indices, including HNSW and DiskANN, as particular specializations of SVG and show that new indices can be derived from the principles behind this specialization. Finally, we propose SVG-L0 that incorporates an $\ell_0$ sparsity constraint into the SVG kernel method to build graphs with a bounded out-degree. This yields a principled way of implementing this practical requirement, in contrast to the traditional heuristic of simply truncating the out edges of each node. Additionally, we show that SVG-L0 has a self-tuning property that avoids the heuristic of using a set of candidates to find the out-edges of each node and that keeps its computational complexity in check.

Toward Optimal Search and Retrieval for RAG

Retrieval-augmented generation (RAG) is a promising method for addressing some of the memory-related challenges associated with Large Language Models (LLMs). Two separate systems form the RAG pipeline, the retriever and the reader, and the impact of each on downstream task performance is not well-understood. Here, we work towards the goal of understanding how retrievers can be optimized for RAG pipelines for common tasks such as Question Answering (QA). We conduct experiments focused on the relationship between retrieval and RAG performance on QA and attributed QA and unveil a number of insights useful to practitioners developing high-performance RAG pipelines. For example, lowering search accuracy has minor implications for RAG performance while potentially increasing retrieval speed and memory efficiency.

Locally-Adaptive Quantization for Streaming Vector Search

Retrieving the most similar vector embeddings to a given query among a massive collection of vectors has long been a key component of countless real-world applications. The recently introduced Retrieval-Augmented Generation is one of the most prominent examples. For many of these applications, the database evolves over time by inserting new data and removing outdated data. In these cases, the retrieval problem is known as streaming similarity search. While Locally-Adaptive Vector Quantization (LVQ), a highly efficient vector compression method, yields state-of-the-art search performance for non-evolving databases, its usefulness in the streaming setting has not been yet established. In this work, we study LVQ in streaming similarity search. In support of our evaluation, we introduce two improvements of LVQ: Turbo LVQ and multi-means LVQ that boost its search performance by up to 28% and 27%, respectively. Our studies show that LVQ and its new variants enable blazing fast vector search, outperforming its closest competitor by up to 9.4x for identically distributed data and by up to 8.8x under the challenging scenario of data distribution shifts (i.e., where the statistical distribution of the data changes over time). We release our contributions as part of Scalable Vector Search, an open-source library for high-performance similarity search.

LeanVec: Search your vectors faster by making them fit

Modern deep learning models have the ability to generate high-dimensional vectors whose similarity reflects semantic resemblance. Thus, similarity search, i.e., the operation of retrieving those vectors in a large collection that are similar to a given query, has become a critical component of a wide range of applications that demand highly accurate and timely answers. In this setting, the high vector dimensionality puts similarity search systems under compute and memory pressure, leading to subpar performance. Additionally, cross-modal retrieval tasks have become increasingly common, e.g., where a user inputs a text query to find the most relevant images for that query. However, these queries often have different distributions than the database embeddings, making it challenging to achieve high accuracy. In this work, we present LeanVec, a framework that combines linear dimensionality reduction with vector quantization to accelerate similarity search on high-dimensional vectors while maintaining accuracy. We present LeanVec variants for in-distribution (ID) and out-of-distribution (OOD) queries. LeanVec-ID yields accuracies on par with those from recently introduced deep learning alternatives whose computational overhead precludes their usage in practice. LeanVec-OOD uses a novel technique for dimensionality reduction that considers the query and database distributions to simultaneously boost the accuracy and the performance of the framework even further (even presenting competitive results when the query and database distributions match). All in all, our extensive and varied experimental results show that LeanVec produces state-of-the-art results, with up to 3.7x improvement in search throughput and up to 4.9x faster index build time over the state of the art.

CoLiDE: Concomitant Linear DAG Estimation

We deal with the combinatorial problem of learning directed acyclic graph (DAG) structure from observational data adhering to a linear structural equation model (SEM). Leveraging advances in differentiable, nonconvex characterizations of acyclicity, recent efforts have advocated a continuous constrained optimization paradigm to efficiently explore the space of DAGs. Most existing methods employ lasso-type score functions to guide this search, which (i) require expensive penalty parameter retuning when the $\textit{unknown}$ SEM noise variances change across problem instances; and (ii) implicitly rely on limiting homoscedasticity assumptions. In this work, we propose a new convex score function for sparsity-aware learning of linear DAGs, which incorporates concomitant estimation of scale and thus effectively decouples the sparsity parameter from the exogenous noise levels. Regularization via a smooth, nonconvex acyclicity penalty term yields CoLiDE ($\textbf{Co}$ncomitant $\textbf{Li}$near $\textbf{D}$AG $\textbf{E}$stimation), a regression-based criterion amenable to efficient gradient computation and closed-form estimation of noise variances in heteroscedastic scenarios. Our algorithm outperforms state-of-the-art methods without incurring added complexity, especially when the DAGs are larger and the noise level profile is heterogeneous. We also find CoLiDE exhibits enhanced stability manifested via reduced standard deviations in several domain-specific metrics, underscoring the robustness of our novel linear DAG estimator.

Similarity search in the blink of an eye with compressed indices

Nowadays, data is represented by vectors. Retrieving those vectors, among millions and billions, that are similar to a given query is a ubiquitous problem of relevance for a wide range of applications. In this work, we present new techniques for creating faster and smaller indices to run these searches. To this end, we introduce a novel vector compression method, Locally-adaptive Vector Quantization (LVQ), that simultaneously reduces memory footprint and improves search performance, with minimal impact on search accuracy. LVQ is designed to work optimally in conjunction with graph-based indices, reducing their effective bandwidth while enabling random-access-friendly fast similarity computations. Our experimental results show that LVQ, combined with key optimizations for graph-based indices in modern datacenter systems, establishes the new state of the art in terms of performance and memory footprint. For billions of vectors, LVQ outcompetes the second-best alternatives: (1) in the low-memory regime, by up to 20.7x in throughput with up to a 3x memory footprint reduction, and (2) in the high-throughput regime by 5.8x with 1.4x less memory.

Toward a Geometrical Understanding of Self-supervised Contrastive Learning

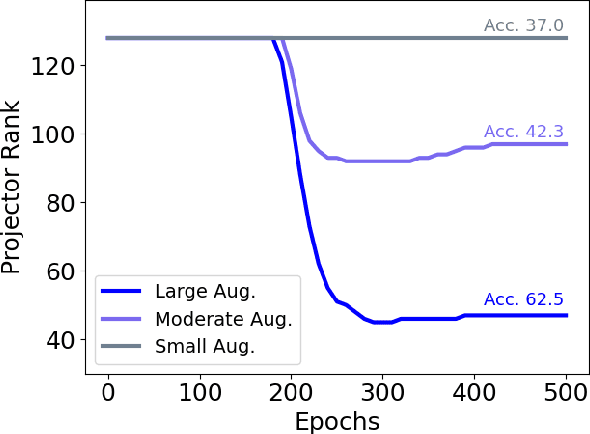
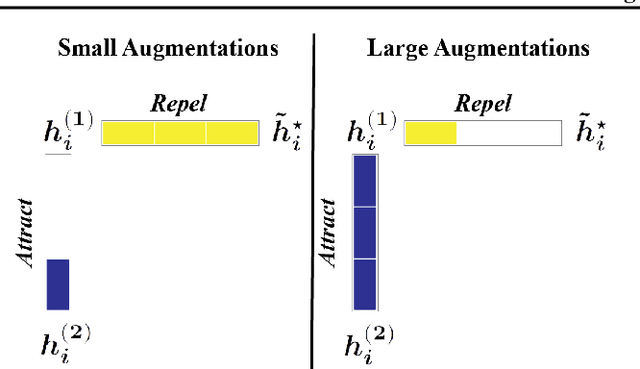
Self-supervised learning (SSL) is currently one of the premier techniques to create data representations that are actionable for transfer learning in the absence of human annotations. Despite their success, the underlying geometry of these representations remains elusive, which obfuscates the quest for more robust, trustworthy, and interpretable models. In particular, mainstream SSL techniques rely on a specific deep neural network architecture with two cascaded neural networks: the encoder and the projector. When used for transfer learning, the projector is discarded since empirical results show that its representation generalizes more poorly than the encoder's. In this paper, we investigate this curious phenomenon and analyze how the strength of the data augmentation policies affects the data embedding. We discover a non-trivial relation between the encoder, the projector, and the data augmentation strength: with increasingly larger augmentation policies, the projector, rather than the encoder, is more strongly driven to become invariant to the augmentations. It does so by eliminating crucial information about the data by learning to project it into a low-dimensional space, a noisy estimate of the data manifold tangent plane in the encoder representation. This analysis is substantiated through a geometrical perspective with theoretical and empirical results.

Procrustean Orthogonal Sparse Hashing

Hashing is one of the most popular methods for similarity search because of its speed and efficiency. Dense binary hashing is prevalent in the literature. Recently, insect olfaction was shown to be structurally and functionally analogous to sparse hashing [6]. Here, we prove that this biological mechanism is the solution to a well-posed optimization problem. Furthermore, we show that orthogonality increases the accuracy of sparse hashing. Next, we present a novel method, Procrustean Orthogonal Sparse Hashing (POSH), that unifies these findings, learning an orthogonal transform from training data compatible with the sparse hashing mechanism. We provide theoretical evidence of the shortcomings of Optimal Sparse Lifting (OSL) [22] and BioHash [30], two related olfaction-inspired methods, and propose two new methods, Binary OSL and SphericalHash, to address these deficiencies. We compare POSH, Binary OSL, and SphericalHash to several state-of-the-art hashing methods and provide empirical results for the superiority of the proposed methods across a wide range of standard benchmarks and parameter settings.

Do place cells dream of conditional probabilities? Learning Neural Nyström representations

We posit that hippocampal place cells encode information about future locations under a transition distribution observed as an agent explores a given (physical or conceptual) space. The encoding of information about the current location, usually associated with place cells, then emerges as a necessary step to achieve this broader goal. We formally derive a biologically-inspired neural network from Nystr\"om kernel approximations and empirically demonstrate that the network successfully approximates transition distributions. The proposed network yields representations that, just like place cells, soft-tile the input space with highly sparse and localized receptive fields. Additionally, we show that the proposed computational motif can be extended to handle supervised problems, creating class-specific place cells while exhibiting low sample complexity.

Clustering is semidefinitely not that hard: Nonnegative SDP for manifold disentangling

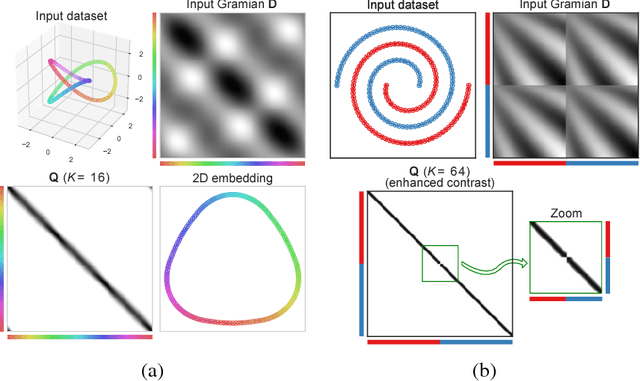
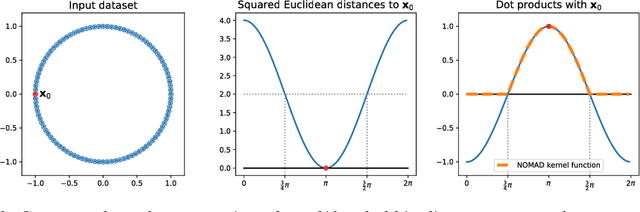
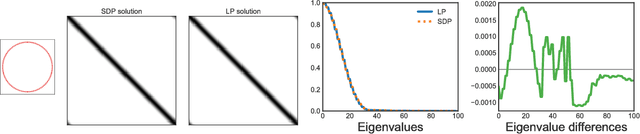
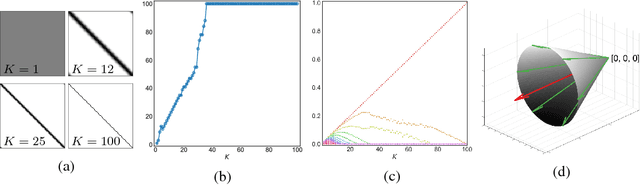
In solving hard computational problems, semidefinite program (SDP) relaxations often play an important role because they come with a guarantee of optimality. Here, we focus on a popular semidefinite relaxation of K-means clustering which yields the same solution as the non-convex original formulation for well segregated datasets. We report an unexpected finding: when data contains (greater than zero-dimensional) manifolds, the SDP solution captures such geometrical structures. Unlike traditional manifold embedding techniques, our approach does not rely on manually defining a kernel but rather enforces locality via a nonnegativity constraint. We thus call our approach NOnnegative MAnifold Disentangling, or NOMAD. To build an intuitive understanding of its manifold learning capabilities, we develop a theoretical analysis of NOMAD on idealized datasets. While NOMAD is convex and the globally optimal solution can be found by generic SDP solvers with polynomial time complexity, they are too slow for modern datasets. To address this problem, we analyze a non-convex heuristic and present a new, convex and yet efficient, algorithm, based on the conditional gradient method. Our results render NOMAD a versatile, understandable, and powerful tool for manifold learning.