Echoing: Identity Failures when LLM Agents Talk to Each Other

As large language model (LLM) based agents interact autonomously with one another, a new class of failures emerges that cannot be predicted from single agent performance: behavioral drifts in agent-agent conversations (AxA). Unlike human-agent interactions, where humans ground and steer conversations, AxA lacks such stabilizing signals, making these failures unique. We investigate one such failure, echoing, where agents abandon their assigned roles and instead mirror their conversational partners, undermining their intended objectives. Through experiments across $60$ AxA configurations, $3$ domains, and $2000+$ conversations, we demonstrate that echoing occurs across three major LLM providers, with echoing rates from $5\%$ to $70\%$ depending on the model and domain. Moreover, we find that echoing is persistent even in advanced reasoning models with substantial rates ($32.8\%$) that are not reduced by increased reasoning efforts. We analyze prompt impacts, conversation dynamics, showing that echoing arises as interaction grows longer ($7+$ turns in experiments) and is not merely an artifact of sub-optimal prompting. Finally, we introduce a protocol-level mitigation in which targeted use of structured responses reduces echoing to $9\%$.

Convergence dynamics of Agent-to-Agent Interactions with Misaligned objectives

We develop a theoretical framework for agent-to-agent interactions in multi-agent scenarios. We consider the setup in which two language model based agents perform iterative gradient updates toward their respective objectives in-context, using the output of the other agent as input. We characterize the generation dynamics associated with the interaction when the agents have misaligned objectives, and show that this results in a biased equilibrium where neither agent reaches its target - with the residual errors predictable from the objective gap and the geometry induced by the prompt of each agent. We establish the conditions for asymmetric convergence and provide an algorithm that provably achieves an adversarial result, producing one-sided success. Experiments with trained transformer models as well as GPT$5$ for the task of in-context linear regression validate the theory. Our framework presents a setup to study, predict, and defend multi-agent systems; explicitly linking prompt design and interaction setup to stability, bias, and robustness.

AGI Is Coming... Right After AI Learns to Play Wordle

This paper investigates multimodal agents, in particular, OpenAI's Computer-User Agent (CUA), trained to control and complete tasks through a standard computer interface, similar to humans. We evaluated the agent's performance on the New York Times Wordle game to elicit model behaviors and identify shortcomings. Our findings revealed a significant discrepancy in the model's ability to recognize colors correctly depending on the context. The model had a $5.36\%$ success rate over several hundred runs across a week of Wordle. Despite the immense enthusiasm surrounding AI agents and their potential to usher in Artificial General Intelligence (AGI), our findings reinforce the fact that even simple tasks present substantial challenges for today's frontier AI models. We conclude with a discussion of the potential underlying causes, implications for future development, and research directions to improve these AI systems.

Reasoning in Large Language Models: A Geometric Perspective

The advancement of large language models (LLMs) for real-world applications hinges critically on enhancing their reasoning capabilities. In this work, we explore the reasoning abilities of large language models (LLMs) through their geometrical understanding. We establish a connection between the expressive power of LLMs and the density of their self-attention graphs. Our analysis demonstrates that the density of these graphs defines the intrinsic dimension of the inputs to the MLP blocks. We demonstrate through theoretical analysis and toy examples that a higher intrinsic dimension implies a greater expressive capacity of the LLM. We further provide empirical evidence linking this geometric framework to recent advancements in methods aimed at enhancing the reasoning capabilities of LLMs.

Characterizing Large Language Model Geometry Solves Toxicity Detection and Generation

Large Language Models~(LLMs) drive current AI breakthroughs despite very little being known about their internal representations, e.g., how to extract a few informative features to solve various downstream tasks. To provide a practical and principled answer, we propose to characterize LLMs from a geometric perspective. We obtain in closed form (i) the intrinsic dimension in which the Multi-Head Attention embeddings are constrained to exist and (ii) the partition and per-region affine mappings of the per-layer feedforward networks. Our results are informative, do not rely on approximations, and are actionable. First, we show that, motivated by our geometric interpretation, we can bypass Llama$2$'s RLHF by controlling its embedding's intrinsic dimension through informed prompt manipulation. Second, we derive $7$ interpretable spline features that can be extracted from any (pre-trained) LLM layer, providing a rich abstract representation of their inputs. Those features alone ($224$ for Mistral-7B and Llama$2$-7B) are sufficient to help solve toxicity detection, infer the domain of the prompt, and even tackle the Jigsaw challenge, which aims at characterizing the type of toxicity of various prompts. Our results demonstrate how, even in large-scale regimes, exact theoretical results can answer practical questions in language models. Code: \url{https://github.com/RandallBalestriero/SplineLLM}.

The Geometry of Self-supervised Learning Models and its Impact on Transfer Learning

Self-supervised learning (SSL) has emerged as a desirable paradigm in computer vision due to the inability of supervised models to learn representations that can generalize in domains with limited labels. The recent popularity of SSL has led to the development of several models that make use of diverse training strategies, architectures, and data augmentation policies with no existing unified framework to study or assess their effectiveness in transfer learning. We propose a data-driven geometric strategy to analyze different SSL models using local neighborhoods in the feature space induced by each. Unlike existing approaches that consider mathematical approximations of the parameters, individual components, or optimization landscape, our work aims to explore the geometric properties of the representation manifolds learned by SSL models. Our proposed manifold graph metrics (MGMs) provide insights into the geometric similarities and differences between available SSL models, their invariances with respect to specific augmentations, and their performances on transfer learning tasks. Our key findings are two fold: (i) contrary to popular belief, the geometry of SSL models is not tied to its training paradigm (contrastive, non-contrastive, and cluster-based); (ii) we can predict the transfer learning capability for a specific model based on the geometric properties of its semantic and augmentation manifolds.

Toward a Geometrical Understanding of Self-supervised Contrastive Learning

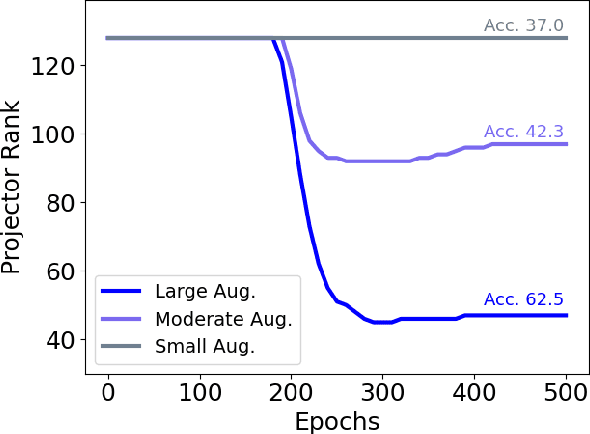
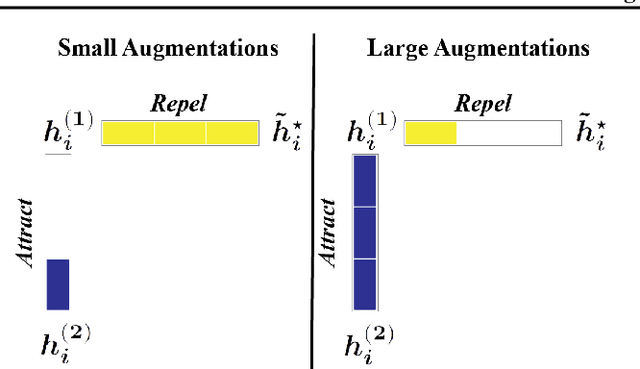
Self-supervised learning (SSL) is currently one of the premier techniques to create data representations that are actionable for transfer learning in the absence of human annotations. Despite their success, the underlying geometry of these representations remains elusive, which obfuscates the quest for more robust, trustworthy, and interpretable models. In particular, mainstream SSL techniques rely on a specific deep neural network architecture with two cascaded neural networks: the encoder and the projector. When used for transfer learning, the projector is discarded since empirical results show that its representation generalizes more poorly than the encoder's. In this paper, we investigate this curious phenomenon and analyze how the strength of the data augmentation policies affects the data embedding. We discover a non-trivial relation between the encoder, the projector, and the data augmentation strength: with increasingly larger augmentation policies, the projector, rather than the encoder, is more strongly driven to become invariant to the augmentations. It does so by eliminating crucial information about the data by learning to project it into a low-dimensional space, a noisy estimate of the data manifold tangent plane in the encoder representation. This analysis is substantiated through a geometrical perspective with theoretical and empirical results.

Spatial Transformer K-Means

K-means defines one of the most employed centroid-based clustering algorithms with performances tied to the data's embedding. Intricate data embeddings have been designed to push $K$-means performances at the cost of reduced theoretical guarantees and interpretability of the results. Instead, we propose preserving the intrinsic data space and augment K-means with a similarity measure invariant to non-rigid transformations. This enables (i) the reduction of intrinsic nuisances associated with the data, reducing the complexity of the clustering task and increasing performances and producing state-of-the-art results, (ii) clustering in the input space of the data, leading to a fully interpretable clustering algorithm, and (iii) the benefit of convergence guarantees.

Interpretable Image Clustering via Diffeomorphism-Aware K-Means

We design an interpretable clustering algorithm aware of the nonlinear structure of image manifolds. Our approach leverages the interpretability of $K$-means applied in the image space while addressing its clustering performance issues. Specifically, we develop a measure of similarity between images and centroids that encompasses a general class of deformations: diffeomorphisms, rendering the clustering invariant to them. Our work leverages the Thin-Plate Spline interpolation technique to efficiently learn diffeomorphisms best characterizing the image manifolds. Extensive numerical simulations show that our approach competes with state-of-the-art methods on various datasets.

Sparse Multi-Family Deep Scattering Network

In this work, we propose the Sparse Multi-Family Deep Scattering Network (SMF-DSN), a novel architecture exploiting the interpretability of the Deep Scattering Network (DSN) and improving its expressive power. The DSN extracts salient and interpretable features in signals by cascading wavelet transforms, complex modulus and extract the representation of the data via a translation-invariant operator. First, leveraging the development of highly specialized wavelet filters over the last decades, we propose a multi-family approach to DSN. In particular, we propose to cross multiple wavelet transforms at each layer of the network, thus increasing the feature diversity and removing the need for an expert to select the appropriate filter. Secondly, we develop an optimal thresholding strategy adequate for the DSN that regularizes the network and controls possible instabilities induced by the signals, such as non-stationary noise. Our systematic and principled solution sparsifies the network's latent representation by acting as a local mask distinguishing between activity and noise. The SMF-DSN enhances the DSN by (i) increasing the diversity of the scattering coefficients and (ii) improves its robustness with respect to non-stationary noise.