Behnaam Aazhang
EMulator: Rapid Estimation of Complex-valued Electric Fields using a U-Net Architecture
May 04, 2025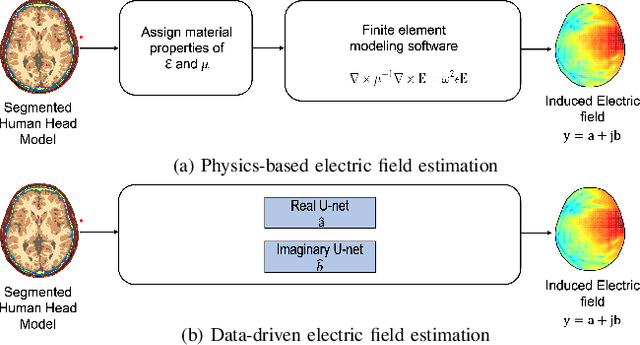
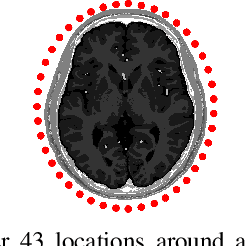

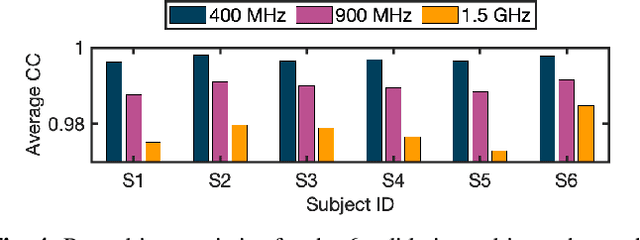
Abstract:A common factor across electromagnetic methodologies of brain stimulation is the optimization of essential dosimetry parameters, like amplitude, phase, and location of one or more transducers, which controls the stimulation strength and targeting precision. Since obtaining in-vivo measurements for the electric field distribution inside the biological tissue is challenging, physics-based simulators are used. However, these simulators are computationally expensive and time-consuming, making repeated calculations of electric fields for optimization purposes computationally prohibitive. To overcome this issue, we developed EMulator, a U-Net architecture-based regression model, for fast and robust complex electric field estimation. We trained EMulator using electric fields generated by 43 antennas placed around 14 segmented human brain models. Once trained, EMulator uses a segmented human brain model with an antenna location as an input and outputs the corresponding electric field. A representative result of our study is that, at 1.5 GHz, on the validation dataset consisting of 6 subjects, we can estimate the electric field with the magnitude of complex correlation coefficient of 0.978. Additionally, we could calculate the electric field with a mean time of 4.4 ms. On average, this is at least x1200 faster than the time required by state-of-the-art physics-based simulator COMSOL. The significance of this work is that it shows the possibility of real-time calculation of the electric field from the segmented human head model and antenna location, making it possible to optimize the amplitude, phase, and location of several different transducers with stochastic gradient descent since our model is almost everywhere differentiable.
Spatial Transformer K-Means
Feb 16, 2022



Abstract:K-means defines one of the most employed centroid-based clustering algorithms with performances tied to the data's embedding. Intricate data embeddings have been designed to push $K$-means performances at the cost of reduced theoretical guarantees and interpretability of the results. Instead, we propose preserving the intrinsic data space and augment K-means with a similarity measure invariant to non-rigid transformations. This enables (i) the reduction of intrinsic nuisances associated with the data, reducing the complexity of the clustering task and increasing performances and producing state-of-the-art results, (ii) clustering in the input space of the data, leading to a fully interpretable clustering algorithm, and (iii) the benefit of convergence guarantees.
RT-RCG: Neural Network and Accelerator Search Towards Effective and Real-time ECG Reconstruction from Intracardiac Electrograms
Nov 04, 2021



Abstract:There exists a gap in terms of the signals provided by pacemakers (i.e., intracardiac electrogram (EGM)) and the signals doctors use (i.e., 12-lead electrocardiogram (ECG)) to diagnose abnormal rhythms. Therefore, the former, even if remotely transmitted, are not sufficient for doctors to provide a precise diagnosis, let alone make a timely intervention. To close this gap and make a heuristic step towards real-time critical intervention in instant response to irregular and infrequent ventricular rhythms, we propose a new framework dubbed RT-RCG to automatically search for (1) efficient Deep Neural Network (DNN) structures and then (2)corresponding accelerators, to enable Real-Time and high-quality Reconstruction of ECG signals from EGM signals. Specifically, RT-RCG proposes a new DNN search space tailored for ECG reconstruction from EGM signals, and incorporates a differentiable acceleration search (DAS) engine to efficiently navigate over the large and discrete accelerator design space to generate optimized accelerators. Extensive experiments and ablation studies under various settings consistently validate the effectiveness of our RT-RCG. To the best of our knowledge, RT-RCG is the first to leverage neural architecture search (NAS) to simultaneously tackle both reconstruction efficacy and efficiency.
Interpretable Image Clustering via Diffeomorphism-Aware K-Means
Dec 16, 2020



Abstract:We design an interpretable clustering algorithm aware of the nonlinear structure of image manifolds. Our approach leverages the interpretability of $K$-means applied in the image space while addressing its clustering performance issues. Specifically, we develop a measure of similarity between images and centroids that encompasses a general class of deformations: diffeomorphisms, rendering the clustering invariant to them. Our work leverages the Thin-Plate Spline interpolation technique to efficiently learn diffeomorphisms best characterizing the image manifolds. Extensive numerical simulations show that our approach competes with state-of-the-art methods on various datasets.
Provable Finite Data Generalization with Group Autoencoder
Sep 20, 2020



Abstract:Deep Autoencoders (AEs) provide a versatile framework to learn a compressed, interpretable, or structured representation of data. As such, AEs have been used extensively for denoising, compression, data completion as well as pre-training of Deep Networks (DNs) for various tasks such as classification. By providing a careful analysis of current AEs from a spline perspective, we can interpret the input-output mapping, in turn allowing us to derive conditions for generalization and reconstruction guarantee. By assuming a Lie group structure on the data at hand, we are able to derive a novel regularization of AEs, allowing for the first time to ensure the generalization of AEs in the finite training set case. We validate our theoretical analysis by demonstrating how this regularization significantly increases the generalization of the AE on various datasets.
The Geometry of Deep Networks: Power Diagram Subdivision
May 21, 2019



Abstract:We study the geometry of deep (neural) networks (DNs) with piecewise affine and convex nonlinearities. The layers of such DNs have been shown to be {\em max-affine spline operators} (MASOs) that partition their input space and apply a region-dependent affine mapping to their input to produce their output. We demonstrate that each MASO layer's input space partitioning corresponds to a {\em power diagram} (an extension of the classical Voronoi tiling) with a number of regions that grows exponentially with respect to the number of units (neurons). We further show that a composition of MASO layers (e.g., the entire DN) produces a progressively subdivided power diagram and provide its analytical form. The subdivision process constrains the affine maps on the (exponentially many) power diagram regions to greatly reduce their complexity. For classification problems, we obtain a formula for a MASO DN's decision boundary in the input space plus a measure of its curvature that depends on the DN's nonlinearities, weights, and architecture. Numerous numerical experiments support and extend our theoretical results.
Robust Unsupervised Transient Detection With Invariant Representation based on the Scattering Network
Nov 23, 2016



Abstract:We present a sparse and invariant representation with low asymptotic complexity for robust unsupervised transient and onset zone detection in noisy environments. This unsupervised approach is based on wavelet transforms and leverages the scattering network from Mallat et al. by deriving frequency invariance. This frequency invariance is a key concept to enforce robust representations of transients in presence of possible frequency shifts and perturbations occurring in the original signal. Implementation details as well as complexity analysis are provided in addition of the theoretical framework and the invariance properties. In this work, our primary application consists of predicting the onset of seizure in epileptic patients from subdural recordings as well as detecting inter-ictal spikes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge