Echoing: Identity Failures when LLM Agents Talk to Each Other

As large language model (LLM) based agents interact autonomously with one another, a new class of failures emerges that cannot be predicted from single agent performance: behavioral drifts in agent-agent conversations (AxA). Unlike human-agent interactions, where humans ground and steer conversations, AxA lacks such stabilizing signals, making these failures unique. We investigate one such failure, echoing, where agents abandon their assigned roles and instead mirror their conversational partners, undermining their intended objectives. Through experiments across $60$ AxA configurations, $3$ domains, and $2000+$ conversations, we demonstrate that echoing occurs across three major LLM providers, with echoing rates from $5\%$ to $70\%$ depending on the model and domain. Moreover, we find that echoing is persistent even in advanced reasoning models with substantial rates ($32.8\%$) that are not reduced by increased reasoning efforts. We analyze prompt impacts, conversation dynamics, showing that echoing arises as interaction grows longer ($7+$ turns in experiments) and is not merely an artifact of sub-optimal prompting. Finally, we introduce a protocol-level mitigation in which targeted use of structured responses reduces echoing to $9\%$.

Convergence dynamics of Agent-to-Agent Interactions with Misaligned objectives

We develop a theoretical framework for agent-to-agent interactions in multi-agent scenarios. We consider the setup in which two language model based agents perform iterative gradient updates toward their respective objectives in-context, using the output of the other agent as input. We characterize the generation dynamics associated with the interaction when the agents have misaligned objectives, and show that this results in a biased equilibrium where neither agent reaches its target - with the residual errors predictable from the objective gap and the geometry induced by the prompt of each agent. We establish the conditions for asymmetric convergence and provide an algorithm that provably achieves an adversarial result, producing one-sided success. Experiments with trained transformer models as well as GPT$5$ for the task of in-context linear regression validate the theory. Our framework presents a setup to study, predict, and defend multi-agent systems; explicitly linking prompt design and interaction setup to stability, bias, and robustness.

AGI Is Coming... Right After AI Learns to Play Wordle

This paper investigates multimodal agents, in particular, OpenAI's Computer-User Agent (CUA), trained to control and complete tasks through a standard computer interface, similar to humans. We evaluated the agent's performance on the New York Times Wordle game to elicit model behaviors and identify shortcomings. Our findings revealed a significant discrepancy in the model's ability to recognize colors correctly depending on the context. The model had a $5.36\%$ success rate over several hundred runs across a week of Wordle. Despite the immense enthusiasm surrounding AI agents and their potential to usher in Artificial General Intelligence (AGI), our findings reinforce the fact that even simple tasks present substantial challenges for today's frontier AI models. We conclude with a discussion of the potential underlying causes, implications for future development, and research directions to improve these AI systems.

Out-of-Distribution Detection through Soft Clustering with Non-Negative Kernel Regression

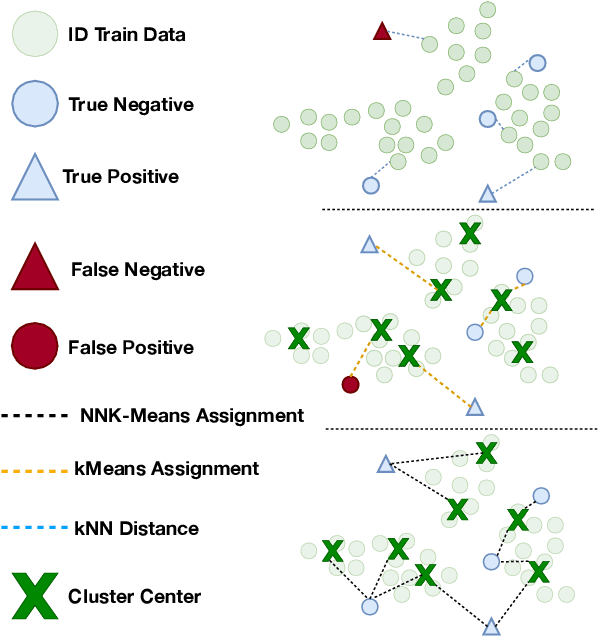
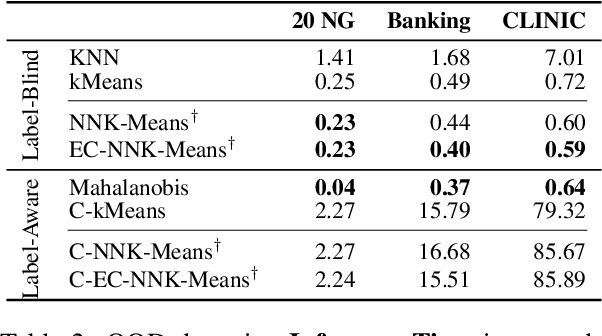
As language models become more general purpose, increased attention needs to be paid to detecting out-of-distribution (OOD) instances, i.e., those not belonging to any of the distributions seen during training. Existing methods for detecting OOD data are computationally complex and storage-intensive. We propose a novel soft clustering approach for OOD detection based on non-negative kernel regression. Our approach greatly reduces computational and space complexities (up to 11x improvement in inference time and 87% reduction in storage requirements) and outperforms existing approaches by up to 4 AUROC points on four different benchmarks. We also introduce an entropy-constrained version of our algorithm, which leads to further reductions in storage requirements (up to 97% lower than comparable approaches) while retaining competitive performance. Our soft clustering approach for OOD detection highlights its potential for detecting tail-end phenomena in extreme-scale data settings.

Reasoning in Large Language Models: A Geometric Perspective

The advancement of large language models (LLMs) for real-world applications hinges critically on enhancing their reasoning capabilities. In this work, we explore the reasoning abilities of large language models (LLMs) through their geometrical understanding. We establish a connection between the expressive power of LLMs and the density of their self-attention graphs. Our analysis demonstrates that the density of these graphs defines the intrinsic dimension of the inputs to the MLP blocks. We demonstrate through theoretical analysis and toy examples that a higher intrinsic dimension implies a greater expressive capacity of the LLM. We further provide empirical evidence linking this geometric framework to recent advancements in methods aimed at enhancing the reasoning capabilities of LLMs.

Towards a geometric understanding of Spatio Temporal Graph Convolution Networks

Spatiotemporal graph convolutional networks (STGCNs) have emerged as a desirable model for skeleton-based human action recognition. Despite achieving state-of-the-art performance, there is a limited understanding of the representations learned by these models, which hinders their application in critical and real-world settings. While layerwise analysis of CNN models has been studied in the literature, to the best of our knowledge, there exists no study on the layerwise explainability of the embeddings learned on spatiotemporal data using STGCNs. In this paper, we first propose to use a local Dataset Graph (DS-Graph) obtained from the feature representation of input data at each layer to develop an understanding of the layer-wise embedding geometry of the STGCN. To do so, we develop a window-based dynamic time warping (DTW) method to compute the distance between data sequences with varying temporal lengths. To validate our findings, we have developed a layer-specific Spatiotemporal Graph Gradient-weighted Class Activation Mapping (L-STG-GradCAM) technique tailored for spatiotemporal data. This approach enables us to visually analyze and interpret each layer within the STGCN network. We characterize the functions learned by each layer of the STGCN using the label smoothness of the representation and visualize them using our L-STG-GradCAM approach. Our proposed method is generic and can yield valuable insights for STGCN architectures in different applications. However, this paper focuses on the human activity recognition task as a representative application. Our experiments show that STGCN models learn representations that capture general human motion in their initial layers while discriminating different actions only in later layers. This justifies experimental observations showing that fine-tuning deeper layers works well for transfer between related tasks.

Characterizing Large Language Model Geometry Solves Toxicity Detection and Generation

Large Language Models~(LLMs) drive current AI breakthroughs despite very little being known about their internal representations, e.g., how to extract a few informative features to solve various downstream tasks. To provide a practical and principled answer, we propose to characterize LLMs from a geometric perspective. We obtain in closed form (i) the intrinsic dimension in which the Multi-Head Attention embeddings are constrained to exist and (ii) the partition and per-region affine mappings of the per-layer feedforward networks. Our results are informative, do not rely on approximations, and are actionable. First, we show that, motivated by our geometric interpretation, we can bypass Llama$2$'s RLHF by controlling its embedding's intrinsic dimension through informed prompt manipulation. Second, we derive $7$ interpretable spline features that can be extracted from any (pre-trained) LLM layer, providing a rich abstract representation of their inputs. Those features alone ($224$ for Mistral-7B and Llama$2$-7B) are sufficient to help solve toxicity detection, infer the domain of the prompt, and even tackle the Jigsaw challenge, which aims at characterizing the type of toxicity of various prompts. Our results demonstrate how, even in large-scale regimes, exact theoretical results can answer practical questions in language models. Code: \url{https://github.com/RandallBalestriero/SplineLLM}.

Study of Manifold Geometry using Multiscale Non-Negative Kernel Graphs

Modern machine learning systems are increasingly trained on large amounts of data embedded in high-dimensional spaces. Often this is done without analyzing the structure of the dataset. In this work, we propose a framework to study the geometric structure of the data. We make use of our recently introduced non-negative kernel (NNK) regression graphs to estimate the point density, intrinsic dimension, and the linearity of the data manifold (curvature). We further generalize the graph construction and geometric estimation to multiple scale by iteratively merging neighborhoods in the input data. Our experiments demonstrate the effectiveness of our proposed approach over other baselines in estimating the local geometry of the data manifolds on synthetic and real datasets.

The Geometry of Self-supervised Learning Models and its Impact on Transfer Learning

Self-supervised learning (SSL) has emerged as a desirable paradigm in computer vision due to the inability of supervised models to learn representations that can generalize in domains with limited labels. The recent popularity of SSL has led to the development of several models that make use of diverse training strategies, architectures, and data augmentation policies with no existing unified framework to study or assess their effectiveness in transfer learning. We propose a data-driven geometric strategy to analyze different SSL models using local neighborhoods in the feature space induced by each. Unlike existing approaches that consider mathematical approximations of the parameters, individual components, or optimization landscape, our work aims to explore the geometric properties of the representation manifolds learned by SSL models. Our proposed manifold graph metrics (MGMs) provide insights into the geometric similarities and differences between available SSL models, their invariances with respect to specific augmentations, and their performances on transfer learning tasks. Our key findings are two fold: (i) contrary to popular belief, the geometry of SSL models is not tied to its training paradigm (contrastive, non-contrastive, and cluster-based); (ii) we can predict the transfer learning capability for a specific model based on the geometric properties of its semantic and augmentation manifolds.

Channel redundancy and overlap in convolutional neural networks with channel-wise NNK graphs

Feature spaces in the deep layers of convolutional neural networks (CNNs) are often very high-dimensional and difficult to interpret. However, convolutional layers consist of multiple channels that are activated by different types of inputs, which suggests that more insights may be gained by studying the channels and how they relate to each other. In this paper, we first analyze theoretically channel-wise non-negative kernel (CW-NNK) regression graphs, which allow us to quantify the overlap between channels and, indirectly, the intrinsic dimension of the data representation manifold. We find that redundancy between channels is significant and varies with the layer depth and the level of regularization during training. Additionally, we observe that there is a correlation between channel overlap in the last convolutional layer and generalization performance. Our experimental results demonstrate that these techniques can lead to a better understanding of deep representations.