Out-of-Distribution Detection through Soft Clustering with Non-Negative Kernel Regression

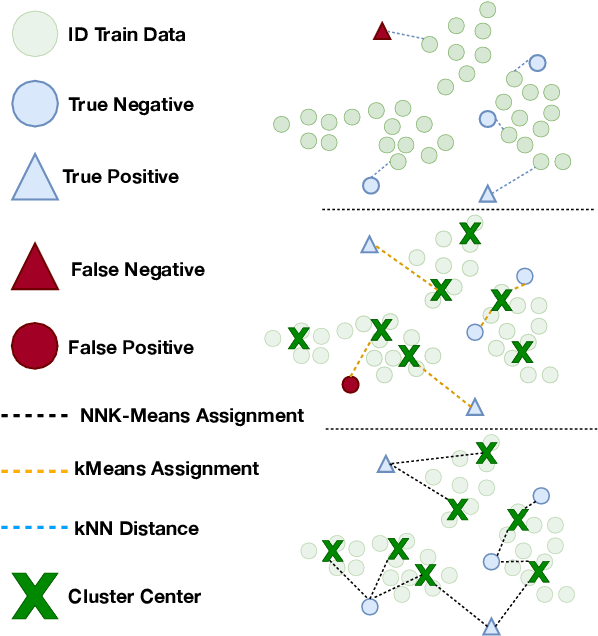
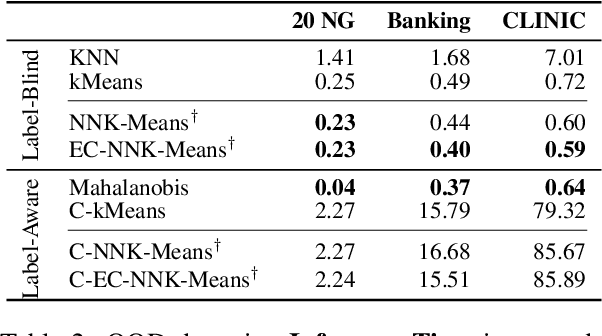
As language models become more general purpose, increased attention needs to be paid to detecting out-of-distribution (OOD) instances, i.e., those not belonging to any of the distributions seen during training. Existing methods for detecting OOD data are computationally complex and storage-intensive. We propose a novel soft clustering approach for OOD detection based on non-negative kernel regression. Our approach greatly reduces computational and space complexities (up to 11x improvement in inference time and 87% reduction in storage requirements) and outperforms existing approaches by up to 4 AUROC points on four different benchmarks. We also introduce an entropy-constrained version of our algorithm, which leads to further reductions in storage requirements (up to 97% lower than comparable approaches) while retaining competitive performance. Our soft clustering approach for OOD detection highlights its potential for detecting tail-end phenomena in extreme-scale data settings.

Study of Manifold Geometry using Multiscale Non-Negative Kernel Graphs

Modern machine learning systems are increasingly trained on large amounts of data embedded in high-dimensional spaces. Often this is done without analyzing the structure of the dataset. In this work, we propose a framework to study the geometric structure of the data. We make use of our recently introduced non-negative kernel (NNK) regression graphs to estimate the point density, intrinsic dimension, and the linearity of the data manifold (curvature). We further generalize the graph construction and geometric estimation to multiple scale by iteratively merging neighborhoods in the input data. Our experiments demonstrate the effectiveness of our proposed approach over other baselines in estimating the local geometry of the data manifolds on synthetic and real datasets.