Non-negative Weighted DAG Structure Learning

We address the problem of learning the topology of directed acyclic graphs (DAGs) from nodal observations, which adhere to a linear structural equation model. Recent advances framed the combinatorial DAG structure learning task as a continuous optimization problem, yet existing methods must contend with the complexities of non-convex optimization. To overcome this limitation, we assume that the latent DAG contains only non-negative edge weights. Leveraging this additional structure, we argue that cycles can be effectively characterized (and prevented) using a convex acyclicity function based on the log-determinant of the adjacency matrix. This convexity allows us to relax the task of learning the non-negative weighted DAG as an abstract convex optimization problem. We propose a DAG recovery algorithm based on the method of multipliers, that is guaranteed to return a global minimizer. Furthermore, we prove that in the infinite sample size regime, the convexity of our approach ensures the recovery of the true DAG structure. We empirically validate the performance of our algorithm in several reproducible synthetic-data test cases, showing that it outperforms state-of-the-art alternatives.

CoLiDE: Concomitant Linear DAG Estimation

We deal with the combinatorial problem of learning directed acyclic graph (DAG) structure from observational data adhering to a linear structural equation model (SEM). Leveraging advances in differentiable, nonconvex characterizations of acyclicity, recent efforts have advocated a continuous constrained optimization paradigm to efficiently explore the space of DAGs. Most existing methods employ lasso-type score functions to guide this search, which (i) require expensive penalty parameter retuning when the $\textit{unknown}$ SEM noise variances change across problem instances; and (ii) implicitly rely on limiting homoscedasticity assumptions. In this work, we propose a new convex score function for sparsity-aware learning of linear DAGs, which incorporates concomitant estimation of scale and thus effectively decouples the sparsity parameter from the exogenous noise levels. Regularization via a smooth, nonconvex acyclicity penalty term yields CoLiDE ($\textbf{Co}$ncomitant $\textbf{Li}$near $\textbf{D}$AG $\textbf{E}$stimation), a regression-based criterion amenable to efficient gradient computation and closed-form estimation of noise variances in heteroscedastic scenarios. Our algorithm outperforms state-of-the-art methods without incurring added complexity, especially when the DAGs are larger and the noise level profile is heterogeneous. We also find CoLiDE exhibits enhanced stability manifested via reduced standard deviations in several domain-specific metrics, underscoring the robustness of our novel linear DAG estimator.

Dual-based Online Learning of Dynamic Network Topologies

We investigate online network topology identification from smooth nodal observations acquired in a streaming fashion. Different from non-adaptive batch solutions, our distinctive goal is to track the (possibly) dynamic adjacency matrix with affordable memory and computational costs by processing signal snapshots online. To this end, we leverage and truncate dual-based proximal gradient (DPG) iterations to solve a composite smoothness-regularized, time-varying inverse problem. Numerical tests with synthetic and real electrocorticography data showcase the effectiveness of the novel lightweight iterations when it comes to tracking slowly-varying network connectivity. We also show that the online DPG algorithm converges faster than a primal-based baseline of comparable complexity. Aligned with reproducible research practices, we share the code developed to produce all figures included in this paper.

Accelerated Graph Learning from Smooth Signals

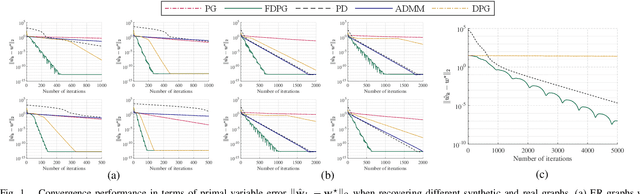
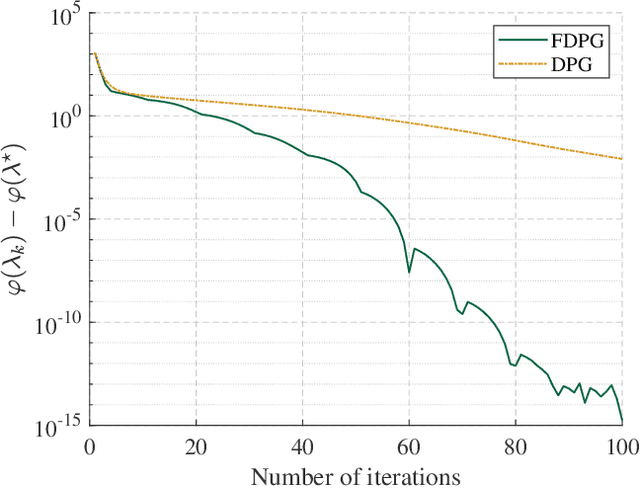
We consider network topology identification subject to a signal smoothness prior on the nodal observations. A fast dual-based proximal gradient algorithm is developed to efficiently tackle a strongly convex, smoothness-regularized network inverse problem known to yield high-quality graph solutions. Unlike existing solvers, the novel iterations come with global convergence rate guarantees and do not require additional step-size tuning. Reproducible simulated tests demonstrate the effectiveness of the proposed method in accurately recovering random and real-world graphs, markedly faster than state-of-the-art alternatives and without incurring an extra computational burden.

Online Graph Learning under Smoothness Priors

The growing success of graph signal processing (GSP) approaches relies heavily on prior identification of a graph over which network data admit certain regularity. However, adaptation to increasingly dynamic environments as well as demands for real-time processing of streaming data pose major challenges to this end. In this context, we develop novel algorithms for online network topology inference given streaming observations assumed to be smooth on the sought graph. Unlike existing batch algorithms, our goal is to track the (possibly) time-varying network topology while maintaining the memory and computational costs in check by processing graph signals sequentially-in-time. To recover the graph in an online fashion, we leverage proximal gradient (PG) methods to solve a judicious smoothness-regularized, time-varying optimization problem. Under mild technical conditions, we establish that the online graph learning algorithm converges to within a neighborhood of (i.e., it tracks) the optimal time-varying batch solution. Computer simulations using both synthetic and real financial market data illustrate the effectiveness of the proposed algorithm in adapting to streaming signals to track slowly-varying network connectivity.

Online Discriminative Graph Learning from Multi-Class Smooth Signals

Graph signal processing (GSP) is a key tool for satisfying the growing demand for information processing over networks. However, the success of GSP in downstream learning and inference tasks is heavily dependent on the prior identification of the relational structures. Graphs are natural descriptors of the relationships between entities of complex environments. The underlying graph is not readily detectable in many cases and one has to infer the topology from the observed signals. Firstly, we address the problem of graph signal classification by proposing a novel framework for discriminative graph learning. To learn discriminative graphs, we invoke the assumption that signals belonging to each class are smooth with respect to the corresponding graph while maintaining non-smoothness with respect to the graphs corresponding to other classes. Secondly, we extend our work to tackle increasingly dynamic environments and real-time topology inference. We develop a proximal gradient (PG) method which can be adapted to situations where the data are acquired on-the-fly. Beyond discrimination, this is the first work that addresses the problem of dynamic graph learning from smooth signals where the sought network alters slowly. The validation of the proposed frameworks is comprehensively investigated using both synthetic and real data.

Segmentation and Classification of Cine-MR Images Using Fully Convolutional Networks and Handcrafted Features

Three-dimensional cine-MRI is of crucial importance for assessing the cardiac function. Features that describe the anatomy and function of cardiac structures (e.g. Left Ventricle (LV), Right Ventricle (RV), and Myocardium(MC)) are known to have significant diagnostic value and can be computed from 3D cine-MR images. However, these features require precise segmentation of cardiac structures. Among the fully automated segmentation methods, Fully Convolutional Networks (FCN) with Skip Connections have shown robustness in medical segmentation problems. In this study, we develop a complete pipeline for classification of subjects with cardiac conditions based on 3D cine-MRI. For the segmentation task, we develop a 2D FCN and introduce Parallel Paths (PP) as a way to exploit the 3D information of the cine-MR image. For the classification task, 125 features were extracted from the segmented structures, describing their anatomy and function. Next, a two-stage pipeline for feature selection using the LASSO method is developed. A subset of 20 features is selected for classification. Each subject is classified using an ensemble of Logistic Regression, Multi-Layer Perceptron, and Support Vector Machine classifiers through majority voting. The Dice Coefficient for segmentation was 0.95+-0.03, 0.89+-0.13, and 0.90+-0.03 for LV, RV, and MC respectively. The 8-fold cross validation accuracy for the classification task was 95.05% and 92.77% based on ground truth and the proposed methods segmentations respectively. The results show that the PPs increase the segmentation accuracy, by exploiting the spatial relations. Moreover, the classification algorithm and the features showed discriminability while keeping the sensitivity to segmentation error as low as possible.