In-context denoising with one-layer transformers: connections between attention and associative memory retrieval

We introduce in-context denoising, a task that refines the connection between attention-based architectures and dense associative memory (DAM) networks, also known as modern Hopfield networks. Using a Bayesian framework, we show theoretically and empirically that certain restricted denoising problems can be solved optimally even by a single-layer transformer. We demonstrate that a trained attention layer processes each denoising prompt by performing a single gradient descent update on a context-aware DAM energy landscape, where context tokens serve as associative memories and the query token acts as an initial state. This one-step update yields better solutions than exact retrieval of either a context token or a spurious local minimum, providing a concrete example of DAM networks extending beyond the standard retrieval paradigm. Overall, this work solidifies the link between associative memory and attention mechanisms first identified by Ramsauer et al., and demonstrates the relevance of associative memory models in the study of in-context learning.

A minimal dynamical system and analog circuit for non-associative learning

Learning in living organisms is typically associated with networks of neurons. The use of large numbers of adjustable units has also been a crucial factor in the continued success of artificial neural networks. In light of the complexity of both living and artificial neural networks, it is surprising to see that very simple organisms -- even unicellular organisms that do not possess a nervous system -- are capable of certain forms of learning. Since in these cases learning may be implemented with much simpler structures than neural networks, it is natural to ask how simple the building blocks required for basic forms of learning may be. The purpose of this study is to discuss the simplest dynamical systems that model a fundamental form of non-associative learning, habituation, and to elucidate technical implementations of such systems, which may be used to implement non-associative learning in neuromorphic computing and related applications.

On the mapping between Hopfield networks and Restricted Boltzmann Machines

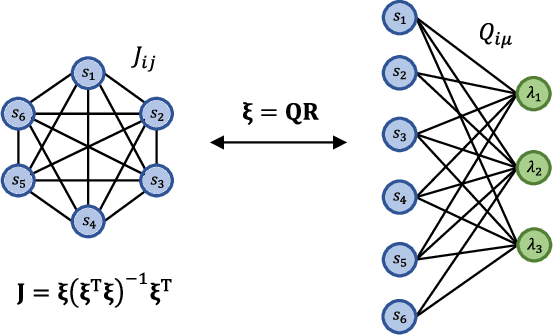
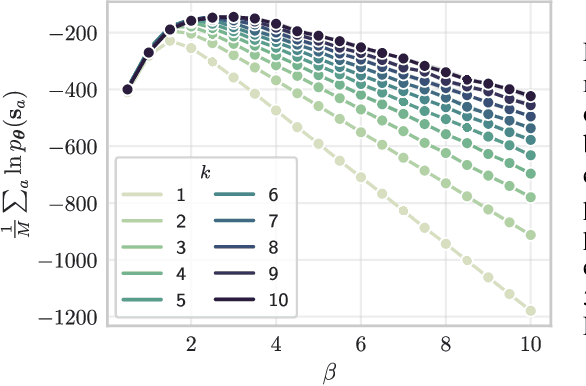
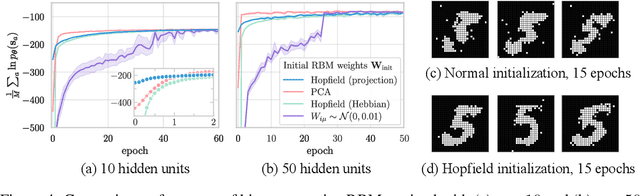
Hopfield networks (HNs) and Restricted Boltzmann Machines (RBMs) are two important models at the interface of statistical physics, machine learning, and neuroscience. Recently, there has been interest in the relationship between HNs and RBMs, due to their similarity under the statistical mechanics formalism. An exact mapping between HNs and RBMs has been previously noted for the special case of orthogonal (uncorrelated) encoded patterns. We present here an exact mapping in the general case of correlated pattern HNs, which are more broadly applicable to existing datasets. Specifically, we show that any HN with $N$ binary variables and $p<N$ arbitrary binary patterns can be transformed into an RBM with $N$ binary visible variables and $p$ gaussian hidden variables. We outline the conditions under which the reverse mapping exists, and conduct experiments on the MNIST dataset which suggest the mapping provides a useful initialization to the RBM weights. We discuss extensions, the potential importance of this correspondence for the training of RBMs, and for understanding the performance of deep architectures which utilize RBMs.