Temporal Wasserstein non-negative matrix factorization for non-rigid motion segmentation and spatiotemporal deconvolution
Paper and Code
Dec 07, 2019
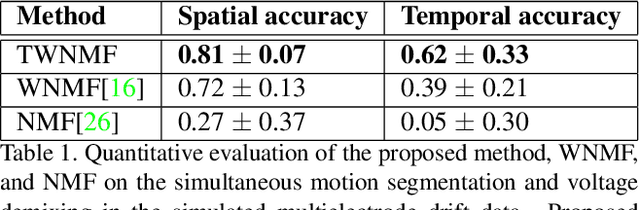

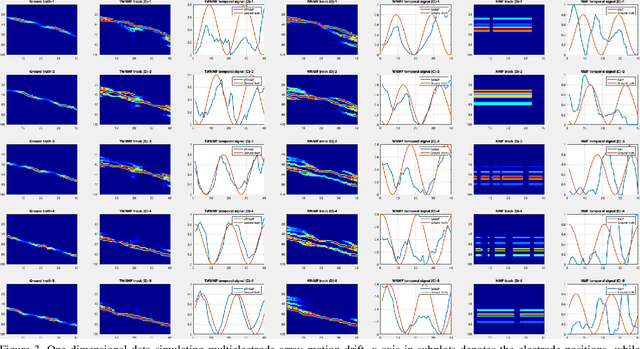
Motion segmentation for natural images commonly relies on dense optic flow to yield point trajectories which can be grouped into clusters through various means including spectral clustering or minimum cost multicuts. However, in biological imaging scenarios, such as fluorescence microscopy or calcium imaging, where the signal to noise ratio is compromised and intensity fluctuations occur, optical flow may be difficult to approximate. To this end, we propose an alternative paradigm for motion segmentation based on optimal transport which models the video frames as time-varying mass represented as histograms. Thus, we cast motion segmentation as a temporal non-linear matrix factorization problem with Wasserstein metric loss. The dictionary elements of this factorization yield segmentation of motion into coherent objects while the loading coefficients allow for time-varying intensity signal of the moving objects to be captured. We demonstrate the use of the proposed paradigm on a simulated multielectrode drift scenario, as well as calcium indicating fluorescence microscopy videos of the nematode Caenorhabditis elegans (C. elegans). The latter application has the added utility of extracting neural activity of the animal in freely conducted behavior.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge