Subtyping brain diseases from imaging data

The imaging community has increasingly adopted machine learning (ML) methods to provide individualized imaging signatures related to disease diagnosis, prognosis, and response to treatment. Clinical neuroscience and cancer imaging have been two areas in which ML has offered particular promise. However, many neurologic and neuropsychiatric diseases, as well as cancer, are often heterogeneous in terms of their clinical manifestations, neuroanatomical patterns or genetic underpinnings. Therefore, in such cases, seeking a single disease signature might be ineffectual in delivering individualized precision diagnostics. The current chapter focuses on ML methods, especially semi-supervised clustering, that seek disease subtypes using imaging data. Work from Alzheimer Disease and its prodromal stages, psychosis, depression, autism, and brain cancer are discussed. Our goal is to provide the readers with a broad overview in terms of methodology and clinical applications.

Multidimensional representations in late-life depression: convergence in neuroimaging, cognition, clinical symptomatology and genetics

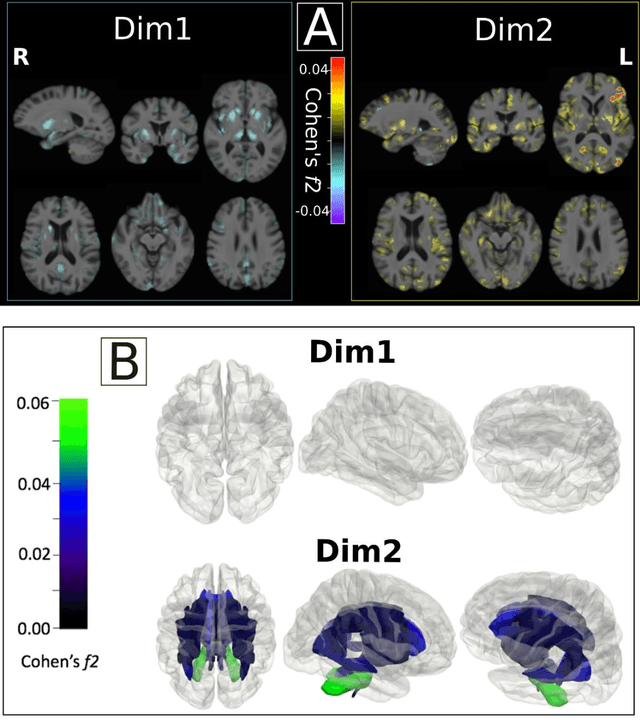
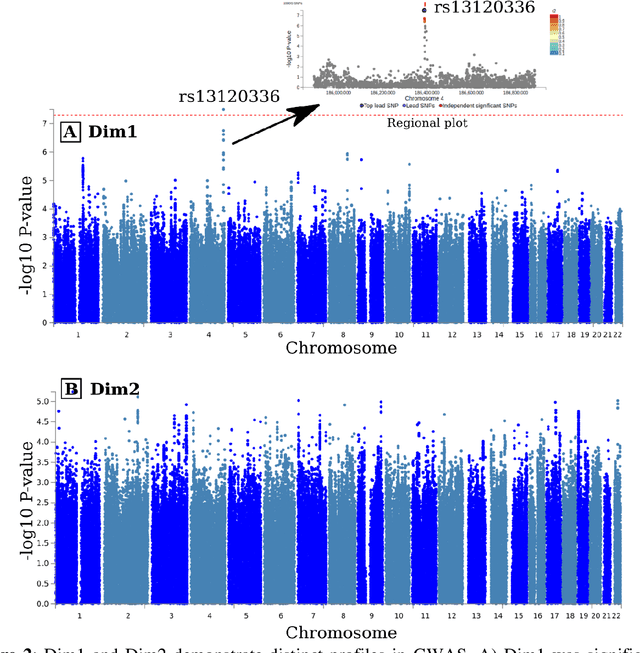
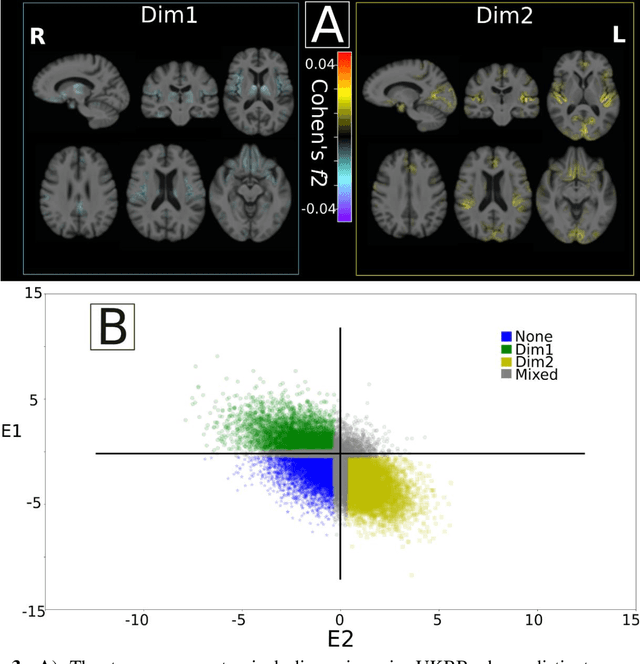
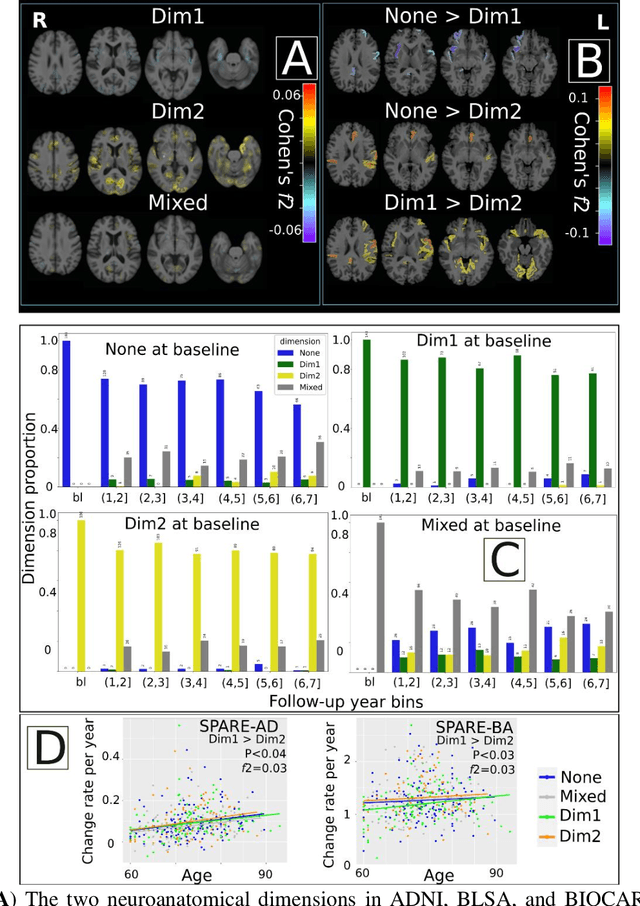
Late-life depression (LLD) is characterized by considerable heterogeneity in clinical manifestation. Unraveling such heterogeneity would aid in elucidating etiological mechanisms and pave the road to precision and individualized medicine. We sought to delineate, cross-sectionally and longitudinally, disease-related heterogeneity in LLD linked to neuroanatomy, cognitive functioning, clinical symptomatology, and genetic profiles. Multimodal data from a multicentre sample (N=996) were analyzed. A semi-supervised clustering method (HYDRA) was applied to regional grey matter (GM) brain volumes to derive dimensional representations. Two dimensions were identified, which accounted for the LLD-related heterogeneity in voxel-wise GM maps, white matter (WM) fractional anisotropy (FA), neurocognitive functioning, clinical phenotype, and genetics. Dimension one (Dim1) demonstrated relatively preserved brain anatomy without WM disruptions relative to healthy controls. In contrast, dimension two (Dim2) showed widespread brain atrophy and WM integrity disruptions, along with cognitive impairment and higher depression severity. Moreover, one de novo independent genetic variant (rs13120336) was significantly associated with Dim 1 but not with Dim 2. Notably, the two dimensions demonstrated significant SNP-based heritability of 18-27% within the general population (N=12,518 in UKBB). Lastly, in a subset of individuals having longitudinal measurements, Dim2 demonstrated a more rapid longitudinal decrease in GM and brain age, and was more likely to progress to Alzheimers disease, compared to Dim1 (N=1,413 participants and 7,225 scans from ADNI, BLSA, and BIOCARD datasets).

MAGIC: Multi-scale Heterogeneity Analysis and Clustering for Brain Diseases

There is a growing amount of clinical, anatomical and functional evidence for the heterogeneous presentation of neuropsychiatric and neurodegenerative diseases such as schizophrenia and Alzheimers Disease (AD). Elucidating distinct subtypes of diseases allows a better understanding of neuropathogenesis and enables the possibility of developing targeted treatment programs. Recent semi-supervised clustering techniques have provided a data-driven way to understand disease heterogeneity. However, existing methods do not take into account that subtypes of the disease might present themselves at different spatial scales across the brain. Here, we introduce a novel method, MAGIC, to uncover disease heterogeneity by leveraging multi-scale clustering. We first extract multi-scale patterns of structural covariance (PSCs) followed by a semi-supervised clustering with double cyclic block-wise optimization across different scales of PSCs. We validate MAGIC using simulated heterogeneous neuroanatomical data and demonstrate its clinical potential by exploring the heterogeneity of AD using T1 MRI scans of 228 cognitively normal (CN) and 191 patients. Our results indicate two main subtypes of AD with distinct atrophy patterns that consist of both fine-scale atrophy in the hippocampus as well as large-scale atrophy in cortical regions. The evidence for the heterogeneity is further corroborated by the clinical evaluation of two subtypes, which indicates that there is a subpopulation of AD patients that tend to be younger and decline faster in cognitive performance relative to the other subpopulation, which tends to be older and maintains a relatively steady decline in cognitive abilities.

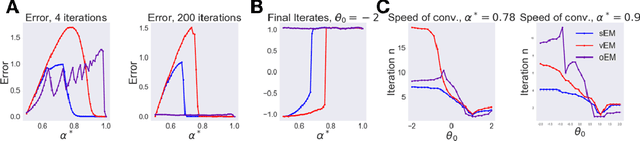
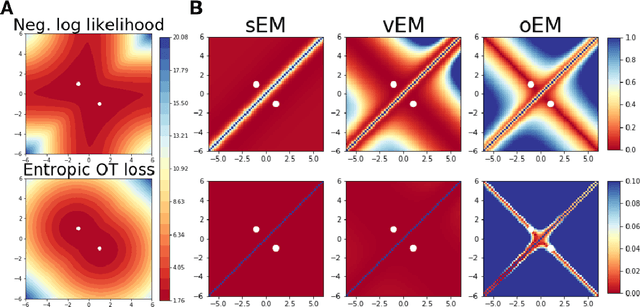
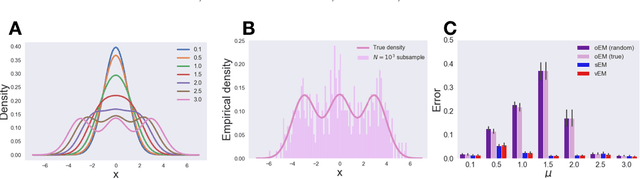
Sinkhorn EM: An Expectation-Maximization algorithm based on entropic optimal transport

We study Sinkhorn EM (sEM), a variant of the expectation maximization (EM) algorithm for mixtures based on entropic optimal transport. sEM differs from the classic EM algorithm in the way responsibilities are computed during the expectation step: rather than assign data points to clusters independently, sEM uses optimal transport to compute responsibilities by incorporating prior information about mixing weights. Like EM, sEM has a natural interpretation as a coordinate ascent procedure, which iteratively constructs and optimizes a lower bound on the log-likelihood. However, we show theoretically and empirically that sEM has better behavior than EM: it possesses better global convergence guarantees and is less prone to getting stuck in bad local optima. We complement these findings with experiments on simulated data as well as in an inference task involving C. elegans neurons and show that sEM learns cell labels significantly better than other approaches.

Temporal Wasserstein non-negative matrix factorization for non-rigid motion segmentation and spatiotemporal deconvolution

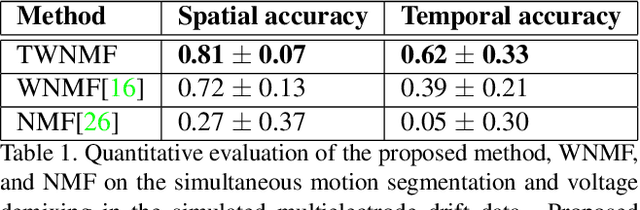
Motion segmentation for natural images commonly relies on dense optic flow to yield point trajectories which can be grouped into clusters through various means including spectral clustering or minimum cost multicuts. However, in biological imaging scenarios, such as fluorescence microscopy or calcium imaging, where the signal to noise ratio is compromised and intensity fluctuations occur, optical flow may be difficult to approximate. To this end, we propose an alternative paradigm for motion segmentation based on optimal transport which models the video frames as time-varying mass represented as histograms. Thus, we cast motion segmentation as a temporal non-linear matrix factorization problem with Wasserstein metric loss. The dictionary elements of this factorization yield segmentation of motion into coherent objects while the loading coefficients allow for time-varying intensity signal of the moving objects to be captured. We demonstrate the use of the proposed paradigm on a simulated multielectrode drift scenario, as well as calcium indicating fluorescence microscopy videos of the nematode Caenorhabditis elegans (C. elegans). The latter application has the added utility of extracting neural activity of the animal in freely conducted behavior.

Wasserstein total variation filtering

In this paper, we expand upon the theory of trend filtering by introducing the use of the Wasserstein metric as a means to control the amount of spatiotemporal variation in filtered time series data. While trend filtering utilizes regularization to produce signal estimates that are piecewise linear, in the case of $\ell_1$ regularization, or temporally smooth, in the case of $\ell_2$ regularization, it ignores the topology of the spatial distribution of signal. By incorporating the information about the underlying metric space of the pixel layout, the Wasserstein metric is an attractive choice as a regularizer to undercover spatiotemporal trends in time series data. We introduce a globally optimal algorithm for efficiently estimating the filtered signal under a Wasserstein finite differences operator. The efficacy of the proposed algorithm in preserving spatiotemporal trends in time series video is demonstrated in both simulated and fluorescent microscopy videos of the nematode caenorhabditis elegans and compared against standard trend filtering algorithms.

Robust approximate linear regression without correspondence

Estimating regression coefficients using unordered multisets of covariates and responses has been introduced as the regression without correspondence problem. Previous theoretical analysis of the problem has been done in a setting where the responses are a permutation of the regressed covariates. This paper expands the setting by analyzing the problem where they may be missing correspondences and outliers in addition to a permutation action. We term this problem robust regression without correspondence and provide several algorithms for exact and approximate recovery in a noiseless and noisy one-dimensional setting as well as an approximation algorithm for multiple dimensions. The theoretical guarantees of the algorithms are verified in simulation data. We also demonstrate a neuroscience application by obtaining robust point set matchings of the neurons of the model organism Caenorhabditis elegans.