Learning Latent Permutations with Gumbel-Sinkhorn Networks
Paper and Code
Feb 23, 2018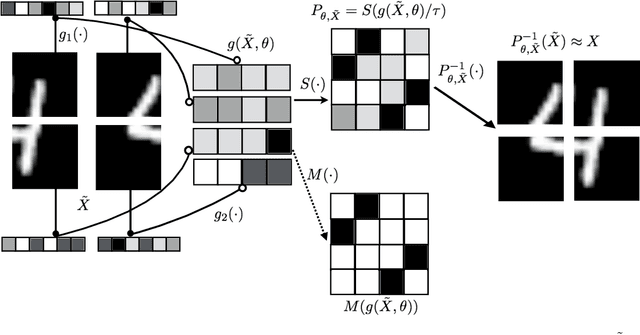



Permutations and matchings are core building blocks in a variety of latent variable models, as they allow us to align, canonicalize, and sort data. Learning in such models is difficult, however, because exact marginalization over these combinatorial objects is intractable. In response, this paper introduces a collection of new methods for end-to-end learning in such models that approximate discrete maximum-weight matching using the continuous Sinkhorn operator. Sinkhorn iteration is attractive because it functions as a simple, easy-to-implement analog of the softmax operator. With this, we can define the Gumbel-Sinkhorn method, an extension of the Gumbel-Softmax method (Jang et al. 2016, Maddison2016 et al. 2016) to distributions over latent matchings. We demonstrate the effectiveness of our method by outperforming competitive baselines on a range of qualitatively different tasks: sorting numbers, solving jigsaw puzzles, and identifying neural signals in worms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge