Yair Weiss
Characterizing Nonlinear Dynamics via Smooth Prototype Equivalences
Mar 13, 2025



Abstract:Characterizing dynamical systems given limited measurements is a common challenge throughout the physical and biological sciences. However, this task is challenging, especially due to transient variability in systems with equivalent long-term dynamics. We address this by introducing smooth prototype equivalences (SPE), a framework that fits a diffeomorphism using normalizing flows to distinct prototypes - simplified dynamical systems that define equivalence classes of behavior. SPE enables classification by comparing the deformation loss of the observed sparse, high-dimensional measurements to the prototype dynamics. Furthermore, our approach enables estimation of the invariant sets of the observed dynamics through the learned mapping from prototype space to data space. Our method outperforms existing techniques in the classification of oscillatory systems and can efficiently identify invariant structures like limit cycles and fixed points in an equation-free manner, even when only a small, noisy subset of the phase space is observed. Finally, we show how our method can be used for the detection of biological processes like the cell cycle trajectory from high-dimensional single-cell gene expression data.
On adversarial training and the 1 Nearest Neighbor classifier
Apr 11, 2024Abstract:The ability to fool deep learning classifiers with tiny perturbations of the input has lead to the development of adversarial training in which the loss with respect to adversarial examples is minimized in addition to the training examples. While adversarial training improves the robustness of the learned classifiers, the procedure is computationally expensive, sensitive to hyperparameters and may still leave the classifier vulnerable to other types of small perturbations. In this paper we analyze the adversarial robustness of the 1 Nearest Neighbor (1NN) classifier and compare its performance to adversarial training. We prove that under reasonable assumptions, the 1 NN classifier will be robust to {\em any} small image perturbation of the training images and will give high adversarial accuracy on test images as the number of training examples goes to infinity. In experiments with 45 different binary image classification problems taken from CIFAR10, we find that 1NN outperform TRADES (a powerful adversarial training algorithm) in terms of average adversarial accuracy. In additional experiments with 69 pretrained robust models for CIFAR10, we find that 1NN outperforms almost all of them in terms of robustness to perturbations that are only slightly different from those seen during training. Taken together, our results suggest that modern adversarial training methods still fall short of the robustness of the simple 1NN classifier. our code can be found at https://github.com/amirhagai/On-Adversarial-Training-And-The-1-Nearest-Neighbor-Classifier
Lost in Translation: Modern Neural Networks Still Struggle With Small Realistic Image Transformations
Apr 10, 2024Abstract:Deep neural networks that achieve remarkable performance in image classification have previously been shown to be easily fooled by tiny transformations such as a one pixel translation of the input image. In order to address this problem, two approaches have been proposed in recent years. The first approach suggests using huge datasets together with data augmentation in the hope that a highly varied training set will teach the network to learn to be invariant. The second approach suggests using architectural modifications based on sampling theory to deal explicitly with image translations. In this paper, we show that these approaches still fall short in robustly handling 'natural' image translations that simulate a subtle change in camera orientation. Our findings reveal that a mere one-pixel translation can result in a significant change in the predicted image representation for approximately 40% of the test images in state-of-the-art models (e.g. open-CLIP trained on LAION-2B or DINO-v2) , while models that are explicitly constructed to be robust to cyclic translations can still be fooled with 1 pixel realistic (non-cyclic) translations 11% of the time. We present Robust Inference by Crop Selection: a simple method that can be proven to achieve any desired level of consistency, although with a modest tradeoff with the model's accuracy. Importantly, we demonstrate how employing this method reduces the ability to fool state-of-the-art models with a 1 pixel translation to less than 5% while suffering from only a 1% drop in classification accuracy. Additionally, we show that our method can be easy adjusted to deal with circular shifts as well. In such case we achieve 100% robustness to integer shifts with state-of-the-art accuracy, and with no need for any further training.
Intriguing Properties of Modern GANs
Feb 21, 2024Abstract:Modern GANs achieve remarkable performance in terms of generating realistic and diverse samples. This has led many to believe that ``GANs capture the training data manifold''. In this work we show that this interpretation is wrong. We empirically show that the manifold learned by modern GANs does not fit the training distribution: specifically the manifold does not pass through the training examples and passes closer to out-of-distribution images than to in-distribution images. We also investigate the distribution over images implied by the prior over the latent codes and study whether modern GANs learn a density that approximates the training distribution. Surprisingly, we find that the learned density is very far from the data distribution and that GANs tend to assign higher density to out-of-distribution images. Finally, we demonstrate that the set of images used to train modern GANs are often not part of the typical set described by the GANs' distribution.
Why do CNNs Learn Consistent Representations in their First Layer Independent of Labels and Architecture?
Jun 06, 2022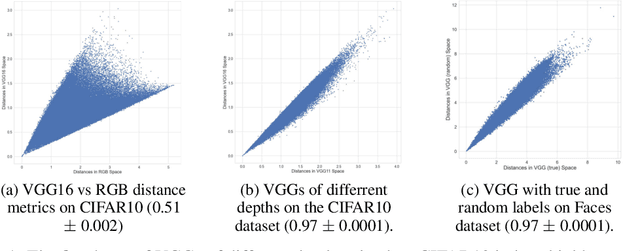
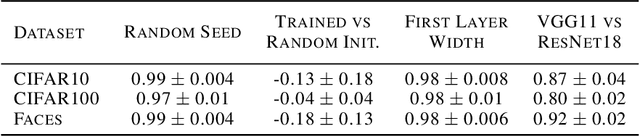
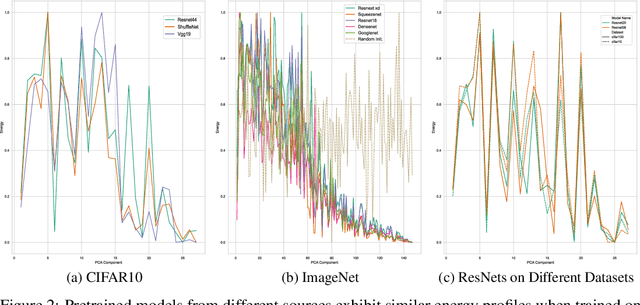

Abstract:It has previously been observed that the filters learned in the first layer of a CNN are qualitatively similar for different networks and tasks. We extend this finding and show a high quantitative similarity between filters learned by different networks. We consider the CNN filters as a filter bank and measure the sensitivity of the filter bank to different frequencies. We show that the sensitivity profile of different networks is almost identical, yet far from initialization. Remarkably, we show that it remains the same even when the network is trained with random labels. To understand this effect, we derive an analytic formula for the sensitivity of the filters in the first layer of a linear CNN. We prove that when the average patch in images of the two classes is identical, the sensitivity profile of the filters in the first layer will be identical in expectation when using the true labels or random labels and will only depend on the second-order statistics of image patches. We empirically demonstrate that the average patch assumption holds for realistic datasets. Finally we show that the energy profile of filters in nonlinear CNNs is highly correlated with the energy profile of linear CNNs and that our analysis of linear networks allows us to predict when representations learned by state-of-the-art networks trained on benchmark classification tasks will depend on the labels.
Generating natural images with direct Patch Distributions Matching
Mar 22, 2022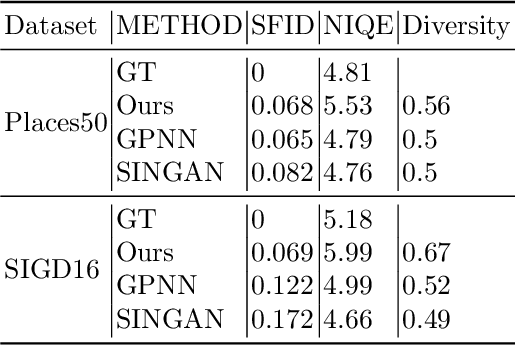


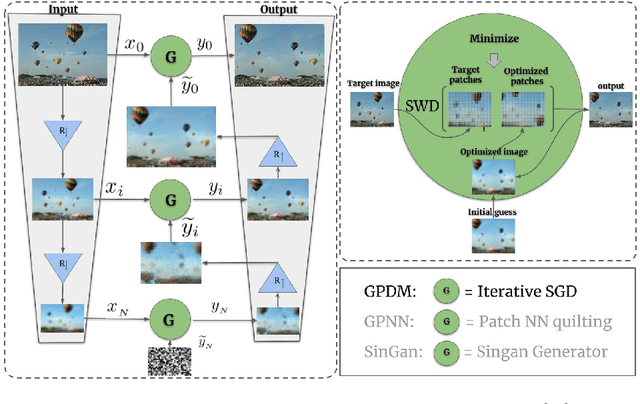
Abstract:Many traditional computer vision algorithms generate realistic images by requiring that each patch in the generated image be similar to a patch in a training image and vice versa. Recently, this classical approach has been replaced by adversarial training with a patch discriminator. The adversarial approach avoids the computational burden of finding nearest neighbors of patches but often requires very long training times and may fail to match the distribution of patches. In this paper we leverage the recently developed Sliced Wasserstein Distance and develop an algorithm that explicitly and efficiently minimizes the distance between patch distributions in two images. Our method is conceptually simple, requires no training and can be implemented in a few lines of codes. On a number of image generation tasks we show that our results are often superior to single-image-GANs, require no training, and can generate high quality images in a few seconds. Our implementation is available at https://github.com/ariel415el/GPDM
Posterior Sampling for Image Restoration using Explicit Patch Priors
Apr 20, 2021


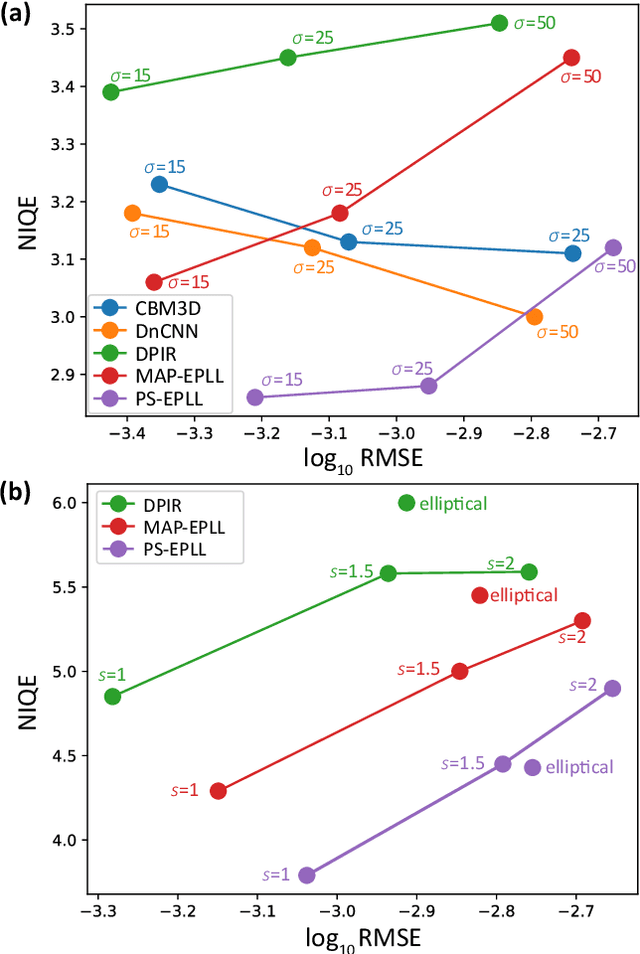
Abstract:Almost all existing methods for image restoration are based on optimizing the mean squared error (MSE), even though it is known that the best estimate in terms of MSE may yield a highly atypical image due to the fact that there are many plausible restorations for a given noisy image. In this paper, we show how to combine explicit priors on patches of natural images in order to sample from the posterior probability of a full image given a degraded image. We prove that our algorithm generates correct samples from the distribution $p(x|y) \propto \exp(-E(x|y))$ where $E(x|y)$ is the cost function minimized in previous patch-based approaches that compute a single restoration. Unlike previous approaches that computed a single restoration using MAP or MMSE, our method makes explicit the uncertainty in the restored images and guarantees that all patches in the restored images will be typical given the patch prior. Unlike previous approaches that used implicit priors on fixed-size images, our approach can be used with images of any size. Our experimental results show that posterior sampling using patch priors yields images of high perceptual quality and high PSNR on a range of challenging image restoration problems.
The Surprising Effectiveness of Linear Unsupervised Image-to-Image Translation
Jul 24, 2020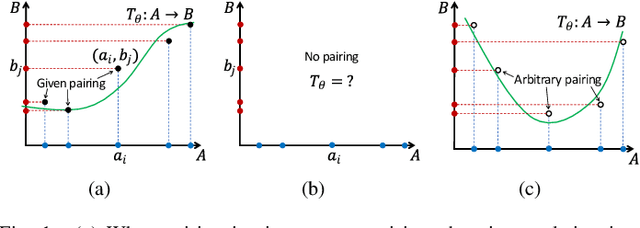



Abstract:Unsupervised image-to-image translation is an inherently ill-posed problem. Recent methods based on deep encoder-decoder architectures have shown impressive results, but we show that they only succeed due to a strong locality bias, and they fail to learn very simple nonlocal transformations (e.g. mapping upside down faces to upright faces). When the locality bias is removed, the methods are too powerful and may fail to learn simple local transformations. In this paper we introduce linear encoder-decoder architectures for unsupervised image to image translation. We show that learning is much easier and faster with these architectures and yet the results are surprisingly effective. In particular, we show a number of local problems for which the results of the linear methods are comparable to those of state-of-the-art architectures but with a fraction of the training time, and a number of nonlocal problems for which the state-of-the-art fails while linear methods succeed.
A Bayes-Optimal View on Adversarial Examples
Feb 20, 2020
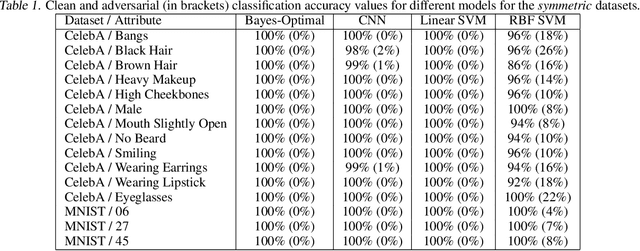

Abstract:The ability to fool modern CNN classifiers with tiny perturbations of the input has lead to the development of a large number of candidate defenses and often conflicting explanations. In this paper, we argue for examining adversarial examples from the perspective of Bayes-Optimal classification. We construct realistic image datasets for which the Bayes-Optimal classifier can be efficiently computed and derive analytic conditions on the distributions so that the optimal classifier is either robust or vulnerable. By training different classifiers on these datasets (for which the "gold standard" optimal classifiers are known), we can disentangle the possible sources of vulnerability and avoid the accuracy-robustness tradeoff that may occur in commonly used datasets. Our results show that even when the optimal classifier is robust, standard CNN training consistently learns a vulnerable classifier. At the same time, for exactly the same training data, RBF SVMs consistently learn a robust classifier. The same trend is observed in experiments with real images.
On GANs and GMMs
Nov 03, 2018
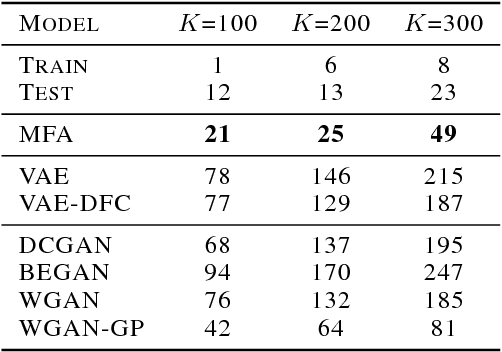
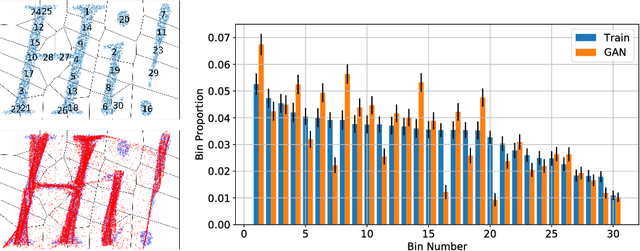

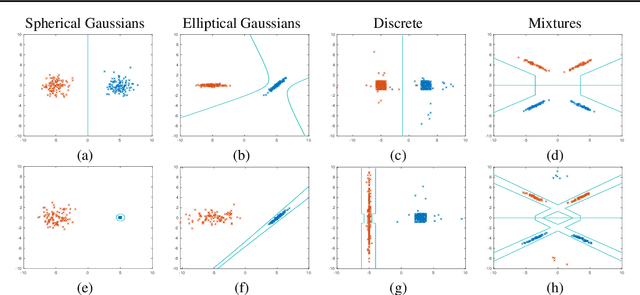
Abstract:A longstanding problem in machine learning is to find unsupervised methods that can learn the statistical structure of high dimensional signals. In recent years, GANs have gained much attention as a possible solution to the problem, and in particular have shown the ability to generate remarkably realistic high resolution sampled images. At the same time, many authors have pointed out that GANs may fail to model the full distribution ("mode collapse") and that using the learned models for anything other than generating samples may be very difficult. In this paper, we examine the utility of GANs in learning statistical models of images by comparing them to perhaps the simplest statistical model, the Gaussian Mixture Model. First, we present a simple method to evaluate generative models based on relative proportions of samples that fall into predetermined bins. Unlike previous automatic methods for evaluating models, our method does not rely on an additional neural network nor does it require approximating intractable computations. Second, we compare the performance of GANs to GMMs trained on the same datasets. While GMMs have previously been shown to be successful in modeling small patches of images, we show how to train them on full sized images despite the high dimensionality. Our results show that GMMs can generate realistic samples (although less sharp than those of GANs) but also capture the full distribution, which GANs fail to do. Furthermore, GMMs allow efficient inference and explicit representation of the underlying statistical structure. Finally, we discuss how GMMs can be used to generate sharp images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge