Inferring biological processes with intrinsic noise from cross-sectional data

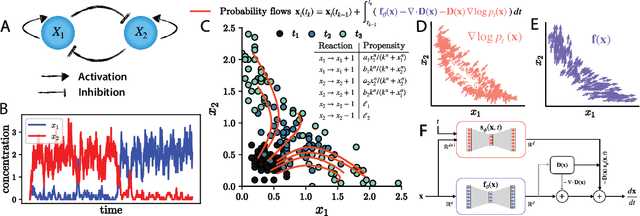
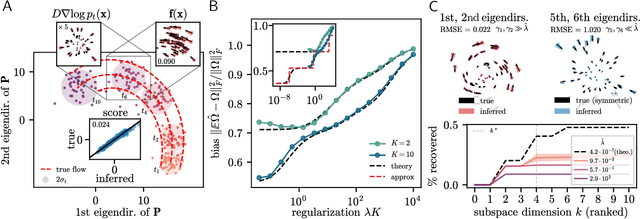
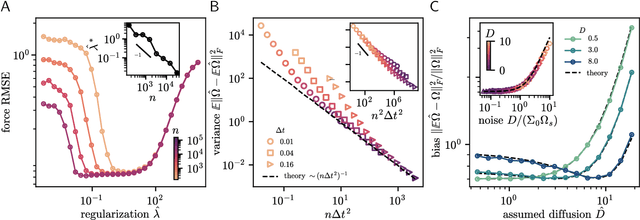
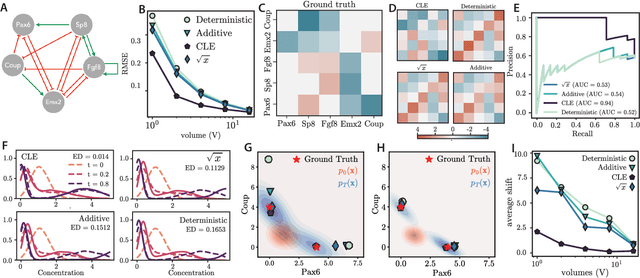
Inferring dynamical models from data continues to be a significant challenge in computational biology, especially given the stochastic nature of many biological processes. We explore a common scenario in omics, where statistically independent cross-sectional samples are available at a few time points, and the goal is to infer the underlying diffusion process that generated the data. Existing inference approaches often simplify or ignore noise intrinsic to the system, compromising accuracy for the sake of optimization ease. We circumvent this compromise by inferring the phase-space probability flow that shares the same time-dependent marginal distributions as the underlying stochastic process. Our approach, probability flow inference (PFI), disentangles force from intrinsic stochasticity while retaining the algorithmic ease of ODE inference. Analytically, we prove that for Ornstein-Uhlenbeck processes the regularized PFI formalism yields a unique solution in the limit of well-sampled distributions. In practical applications, we show that PFI enables accurate parameter and force estimation in high-dimensional stochastic reaction networks, and that it allows inference of cell differentiation dynamics with molecular noise, outperforming state-of-the-art approaches.

Stochastic force inference via density estimation

Inferring dynamical models from low-resolution temporal data continues to be a significant challenge in biophysics, especially within transcriptomics, where separating molecular programs from noise remains an important open problem. We explore a common scenario in which we have access to an adequate amount of cross-sectional samples at a few time-points, and assume that our samples are generated from a latent diffusion process. We propose an approach that relies on the probability flow associated with an underlying diffusion process to infer an autonomous, nonlinear force field interpolating between the distributions. Given a prior on the noise model, we employ score-matching to differentiate the force field from the intrinsic noise. Using relevant biophysical examples, we demonstrate that our approach can extract non-conservative forces from non-stationary data, that it learns equilibrium dynamics when applied to steady-state data, and that it can do so with both additive and multiplicative noise models.

Learning locally dominant force balances in active particle systems

We use a combination of unsupervised clustering and sparsity-promoting inference algorithms to learn locally dominant force balances that explain macroscopic pattern formation in self-organized active particle systems. The self-organized emergence of macroscopic patterns from microscopic interactions between self-propelled particles can be widely observed nature. Although hydrodynamic theories help us better understand the physical basis of this phenomenon, identifying a sufficient set of local interactions that shape, regulate, and sustain self-organized structures in active particle systems remains challenging. We investigate a classic hydrodynamic model of self-propelled particles that produces a wide variety of patterns, like asters and moving density bands. Our data-driven analysis shows that propagating bands are formed by local alignment interactions driven by density gradients, while steady-state asters are shaped by a mechanism of splay-induced negative compressibility arising from strong particle interactions. Our method also reveals analogous physical principles of pattern formation in a system where the speed of the particle is influenced by local density. This demonstrates the ability of our method to reveal physical commonalities across models. The physical mechanisms inferred from the data are in excellent agreement with analytical scaling arguments and experimental observations.

Learning deterministic hydrodynamic equations from stochastic active particle dynamics

We present a principled data-driven strategy for learning deterministic hydrodynamic models directly from stochastic non-equilibrium active particle trajectories. We apply our method to learning a hydrodynamic model for the propagating density lanes observed in self-propelled particle systems and to learning a continuum description of cell dynamics in epithelial tissues. We also infer from stochastic particle trajectories the latent phoretic fields driving chemotaxis. This demonstrates that statistical learning theory combined with physical priors can enable discovery of multi-scale models of non-equilibrium stochastic processes characteristic of collective movement in living systems.

Parallel Discrete Convolutions on Adaptive Particle Representations of Images

We present data structures and algorithms for native implementations of discrete convolution operators over Adaptive Particle Representations (APR) of images on parallel computer architectures. The APR is a content-adaptive image representation that locally adapts the sampling resolution to the image signal. It has been developed as an alternative to pixel representations for large, sparse images as they typically occur in fluorescence microscopy. It has been shown to reduce the memory and runtime costs of storing, visualizing, and processing such images. This, however, requires that image processing natively operates on APRs, without intermediately reverting to pixels. Designing efficient and scalable APR-native image processing primitives, however, is complicated by the APR's irregular memory structure. Here, we provide the algorithmic building blocks required to efficiently and natively process APR images using a wide range of algorithms that can be formulated in terms of discrete convolutions. We show that APR convolution naturally leads to scale-adaptive algorithms that efficiently parallelize on multi-core CPU and GPU architectures. We quantify the speedups in comparison to pixel-based algorithms and convolutions on evenly sampled data. We achieve pixel-equivalent throughputs of up to 1 TB/s on a single Nvidia GeForce RTX 2080 gaming GPU, requiring up to two orders of magnitude less memory than a pixel-based implementation.

Inverse-Dirichlet Weighting Enables Reliable Training of Physics Informed Neural Networks

We characterize and remedy a failure mode that may arise from multi-scale dynamics with scale imbalances during training of deep neural networks, such as Physics Informed Neural Networks (PINNs). PINNs are popular machine-learning templates that allow for seamless integration of physical equation models with data. Their training amounts to solving an optimization problem over a weighted sum of data-fidelity and equation-fidelity objectives. Conflicts between objectives can arise from scale imbalances, heteroscedasticity in the data, stiffness of the physical equation, or from catastrophic interference during sequential training. We explain the training pathology arising from this and propose a simple yet effective inverse-Dirichlet weighting strategy to alleviate the issue. We compare with Sobolev training of neural networks, providing the baseline of analytically $\boldsymbol{\epsilon}$-optimal training. We demonstrate the effectiveness of inverse-Dirichlet weighting in various applications, including a multi-scale model of active turbulence, where we show orders of magnitude improvement in accuracy and convergence over conventional PINN training. For inverse modeling using sequential training, we find that inverse-Dirichlet weighting protects a PINN against catastrophic forgetting.

STENCIL-NET: Data-driven solution-adaptive discretization of partial differential equations

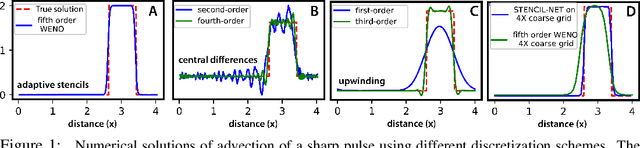
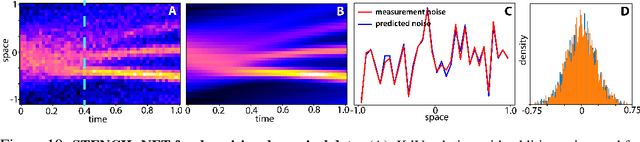
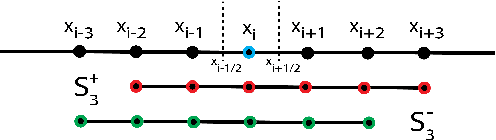
Numerical methods for approximately solving partial differential equations (PDE) are at the core of scientific computing. Often, this requires high-resolution or adaptive discretization grids to capture relevant spatio-temporal features in the PDE solution, e.g., in applications like turbulence, combustion, and shock propagation. Numerical approximation also requires knowing the PDE in order to construct problem-specific discretizations. Systematically deriving such solution-adaptive discrete operators, however, is a current challenge. Here we present STENCIL-NET, an artificial neural network architecture for data-driven learning of problem- and resolution-specific local discretizations of nonlinear PDEs. STENCIL-NET achieves numerically stable discretization of the operators in an unknown nonlinear PDE by spatially and temporally adaptive parametric pooling on regular Cartesian grids, and by incorporating knowledge about discrete time integration. Knowing the actual PDE is not necessary, as solution data is sufficient to train the network to learn the discrete operators. A once-trained STENCIL-NET model can be used to predict solutions of the PDE on larger spatial domains and for longer times than it was trained for, hence addressing the problem of PDE-constrained extrapolation from data. To support this claim, we present numerical experiments on long-term forecasting of chaotic PDE solutions on coarse spatio-temporal grids. We also quantify the speed-up achieved by substituting base-line numerical methods with equation-free STENCIL-NET predictions on coarser grids with little compromise on accuracy.

Learning physically consistent mathematical models from data using group sparsity

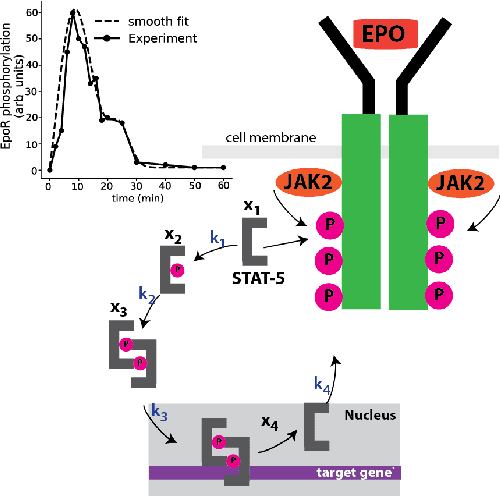
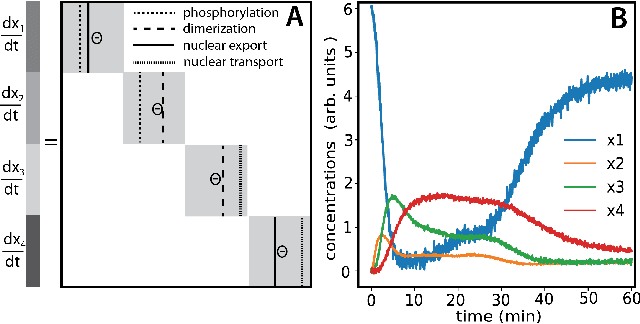
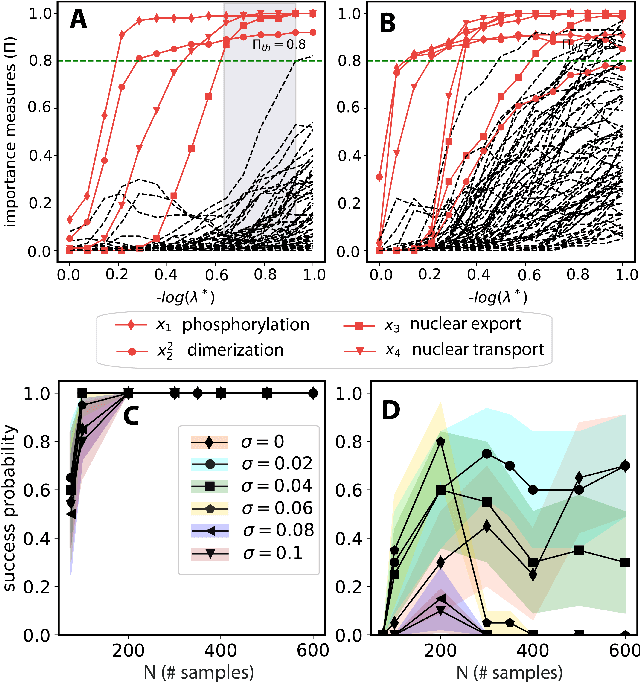
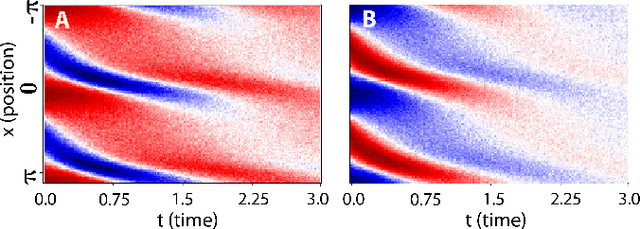
We propose a statistical learning framework based on group-sparse regression that can be used to 1) enforce conservation laws, 2) ensure model equivalence, and 3) guarantee symmetries when learning or inferring differential-equation models from measurement data. Directly learning $\textit{interpretable}$ mathematical models from data has emerged as a valuable modeling approach. However, in areas like biology, high noise levels, sensor-induced correlations, and strong inter-system variability can render data-driven models nonsensical or physically inconsistent without additional constraints on the model structure. Hence, it is important to leverage $\textit{prior}$ knowledge from physical principles to learn "biologically plausible and physically consistent" models rather than models that simply fit the data best. We present a novel group Iterative Hard Thresholding (gIHT) algorithm and use stability selection to infer physically consistent models with minimal parameter tuning. We show several applications from systems biology that demonstrate the benefits of enforcing $\textit{priors}$ in data-driven modeling.

Stability selection enables robust learning of partial differential equations from limited noisy data

We present a statistical learning framework for robust identification of partial differential equations from noisy spatiotemporal data. Extending previous sparse regression approaches for inferring PDE models from simulated data, we address key issues that have thus far limited the application of these methods to noisy experimental data, namely their robustness against noise and the need for manual parameter tuning. We address both points by proposing a stability-based model selection scheme to determine the level of regularization required for reproducible recovery of the underlying PDE. This avoids manual parameter tuning and provides a principled way to improve the method's robustness against noise in the data. Our stability selection approach, termed PDE-STRIDE, can be combined with any sparsity-promoting penalized regression model and provides an interpretable criterion for model component importance. We show that in particular the combination of stability selection with the iterative hard-thresholding algorithm from compressed sensing provides a fast, parameter-free, and robust computational framework for PDE inference that outperforms previous algorithmic approaches with respect to recovery accuracy, amount of data required, and robustness to noise. We illustrate the performance of our approach on a wide range of noise-corrupted simulated benchmark problems, including 1D Burgers, 2D vorticity-transport, and 3D reaction-diffusion problems. We demonstrate the practical applicability of our method on real-world data by considering a purely data-driven re-evaluation of the advective triggering hypothesis for an embryonic polarization system in C.~elegans. Using fluorescence microscopy images of C.~elegans zygotes as input data, our framework is able to recover the PDE model for the regulatory reaction-diffusion-flow network of the associated proteins.