Smoothing the Edges: A General Framework for Smooth Optimization in Sparse Regularization using Hadamard Overparametrization

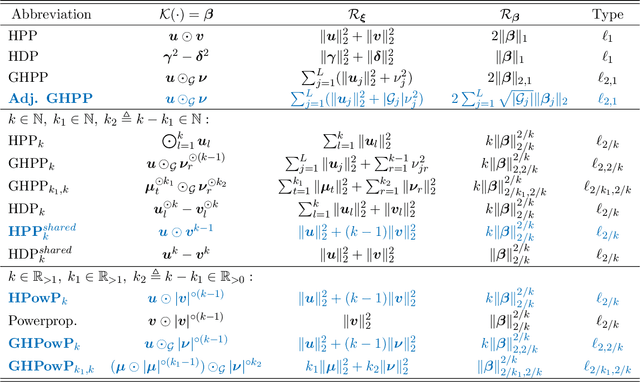
This paper introduces a smooth method for (structured) sparsity in $\ell_q$ and $\ell_{p,q}$ regularized optimization problems. Optimization of these non-smooth and possibly non-convex problems typically relies on specialized procedures. In contrast, our general framework is compatible with prevalent first-order optimization methods like Stochastic Gradient Descent and accelerated variants without any required modifications. This is accomplished through a smooth optimization transfer, comprising an overparametrization of selected model parameters using Hadamard products and a change of penalties. In the overparametrized problem, smooth and convex $\ell_2$ regularization of the surrogate parameters induces non-smooth and non-convex $\ell_q$ or $\ell_{p,q}$ regularization in the original parametrization. We show that our approach yields not only matching global minima but also equivalent local minima. This is particularly useful in non-convex sparse regularization, where finding global minima is NP-hard and local minima are known to generalize well. We provide a comprehensive overview consolidating various literature strands on sparsity-inducing parametrizations and propose meaningful extensions to existing approaches. The feasibility of our approach is evaluated through numerical experiments, which demonstrate that its performance is on par with or surpasses commonly used implementations of convex and non-convex regularization methods.

Factorized Structured Regression for Large-Scale Varying Coefficient Models

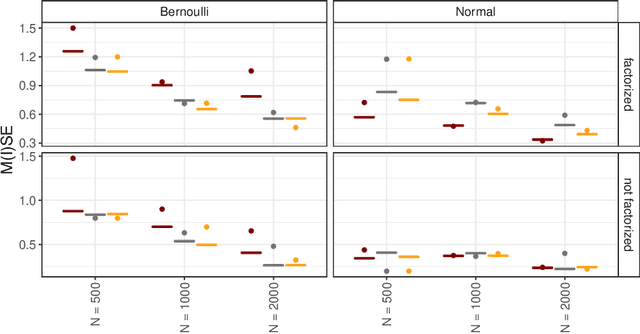
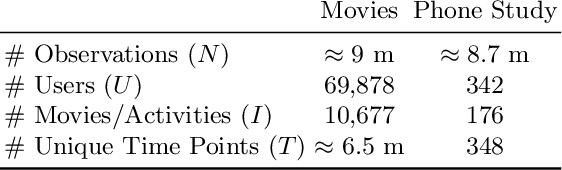
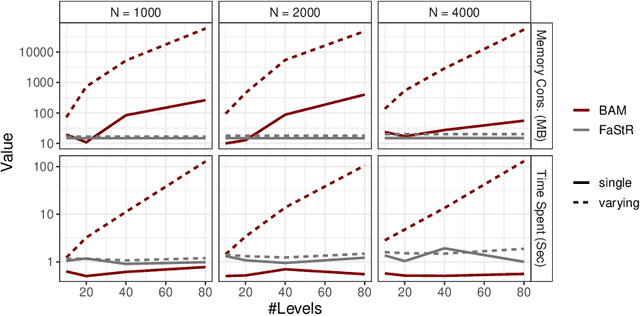
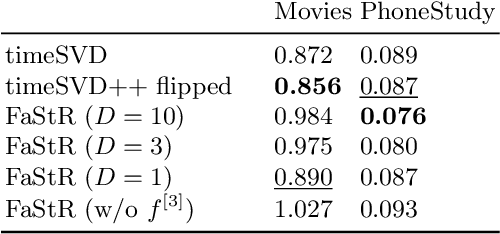
Recommender Systems (RS) pervade many aspects of our everyday digital life. Proposed to work at scale, state-of-the-art RS allow the modeling of thousands of interactions and facilitate highly individualized recommendations. Conceptually, many RS can be viewed as instances of statistical regression models that incorporate complex feature effects and potentially non-Gaussian outcomes. Such structured regression models, including time-aware varying coefficients models, are, however, limited in their applicability to categorical effects and inclusion of a large number of interactions. Here, we propose Factorized Structured Regression (FaStR) for scalable varying coefficient models. FaStR overcomes limitations of general regression models for large-scale data by combining structured additive regression and factorization approaches in a neural network-based model implementation. This fusion provides a scalable framework for the estimation of statistical models in previously infeasible data settings. Empirical results confirm that the estimation of varying coefficients of our approach is on par with state-of-the-art regression techniques, while scaling notably better and also being competitive with other time-aware RS in terms of prediction performance. We illustrate FaStR's performance and interpretability on a large-scale behavioral study with smartphone user data.

Objective hearing threshold identification from auditory brainstem response measurements using supervised and self-supervised approaches

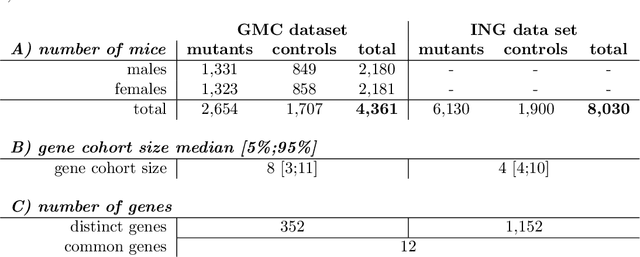
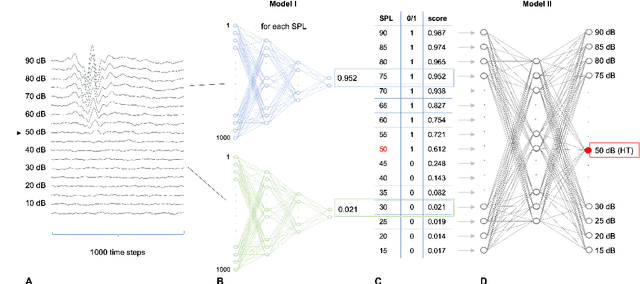
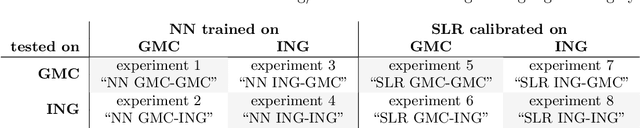
Hearing loss is a major health problem and psychological burden in humans. Mouse models offer a possibility to elucidate genes involved in the underlying developmental and pathophysiological mechanisms of hearing impairment. To this end, large-scale mouse phenotyping programs include auditory phenotyping of single-gene knockout mouse lines. Using the auditory brainstem response (ABR) procedure, the German Mouse Clinic and similar facilities worldwide have produced large, uniform data sets of averaged ABR raw data of mutant and wildtype mice. In the course of standard ABR analysis, hearing thresholds are assessed visually by trained staff from series of signal curves of increasing sound pressure level. This is time-consuming and prone to be biased by the reader as well as the graphical display quality and scale. In an attempt to reduce workload and improve quality and reproducibility, we developed and compared two methods for automated hearing threshold identification from averaged ABR raw data: a supervised approach involving two combined neural networks trained on human-generated labels and a self-supervised approach, which exploits the signal power spectrum and combines random forest sound level estimation with a piece-wise curve fitting algorithm for threshold finding. We show that both models work well, outperform human threshold detection, and are suitable for fast, reliable, and unbiased hearing threshold detection and quality control. In a high-throughput mouse phenotyping environment, both methods perform well as part of an automated end-to-end screening pipeline to detect candidate genes for hearing involvement. Code for both models as well as data used for this work are freely available.

A causal view on compositional data

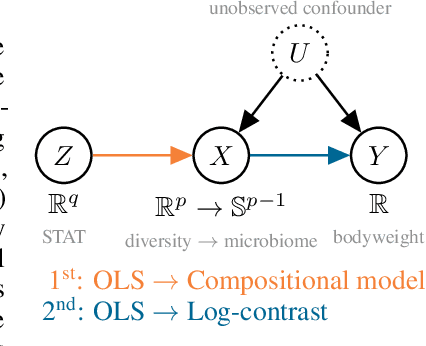
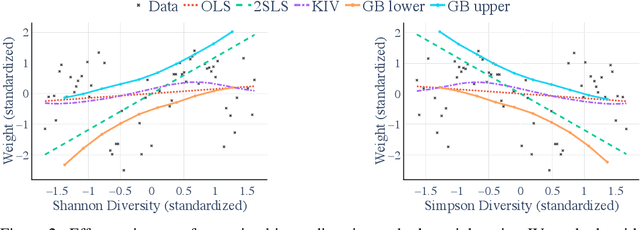
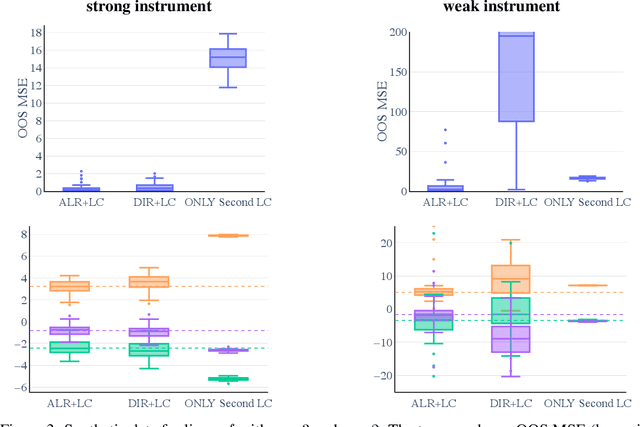
Many scientific datasets are compositional in nature. Important examples include species abundances in ecology, rock compositions in geology, topic compositions in large-scale text corpora, and sequencing count data in molecular biology. Here, we provide a causal view on compositional data in an instrumental variable setting where the composition acts as the cause. Throughout, we pay particular attention to the interpretation of compositional causes from the viewpoint of interventions and crisply articulate potential pitfalls for practitioners. Focusing on modern high-dimensional microbiome sequencing data as a timely illustrative use case, our analysis first reveals that popular one-dimensional information-theoretic summary statistics, such as diversity and richness, may be insufficient for drawing causal conclusions from ecological data. Instead, we advocate for multivariate alternatives using statistical data transformations and regression techniques that take the special structure of the compositional sample space into account. In a comparative analysis on synthetic and semi-synthetic data we show the advantages and limitations of our proposal. We posit that our framework may provide a useful starting point for cause-effect estimation in the context of compositional data.

deepregression: a Flexible Neural Network Framework for Semi-Structured Deep Distributional Regression

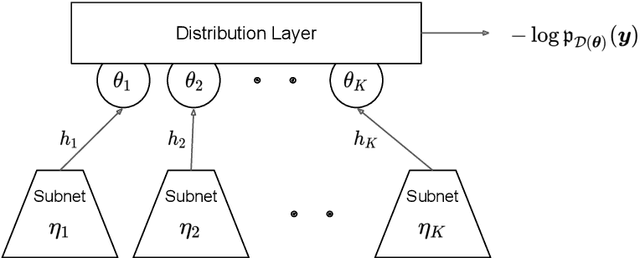
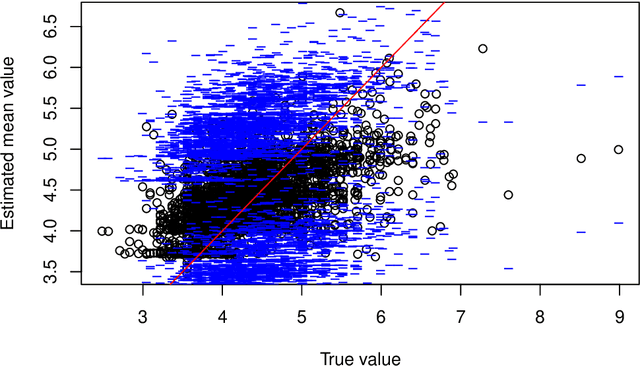
This paper describes the implementation of semi-structured deep distributional regression, a flexible framework to learn distributions based on a combination of additive regression models and deep neural networks. deepregression is implemented in both R and Python, using the deep learning libraries TensorFlow and PyTorch, respectively. The implementation consists of (1) a modular neural network building system for the combination of various statistical and deep learning approaches, (2) an orthogonalization cell to allow for an interpretable combination of different subnetworks as well as (3) pre-processing steps necessary to initialize such models. The software package allows to define models in a user-friendly manner using distribution definitions via a formula environment that is inspired by classical statistical model frameworks such as mgcv. The packages' modular design and functionality provides a unique resource for rapid and reproducible prototyping of complex statistical and deep learning models while simultaneously retaining the indispensable interpretability of classical statistical models.

STENCIL-NET: Data-driven solution-adaptive discretization of partial differential equations

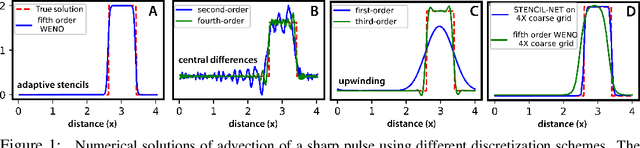
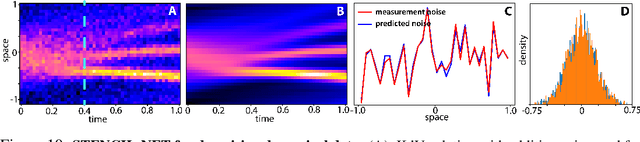
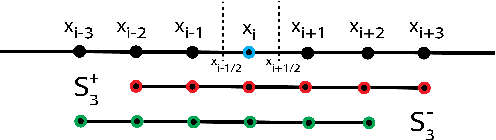
Numerical methods for approximately solving partial differential equations (PDE) are at the core of scientific computing. Often, this requires high-resolution or adaptive discretization grids to capture relevant spatio-temporal features in the PDE solution, e.g., in applications like turbulence, combustion, and shock propagation. Numerical approximation also requires knowing the PDE in order to construct problem-specific discretizations. Systematically deriving such solution-adaptive discrete operators, however, is a current challenge. Here we present STENCIL-NET, an artificial neural network architecture for data-driven learning of problem- and resolution-specific local discretizations of nonlinear PDEs. STENCIL-NET achieves numerically stable discretization of the operators in an unknown nonlinear PDE by spatially and temporally adaptive parametric pooling on regular Cartesian grids, and by incorporating knowledge about discrete time integration. Knowing the actual PDE is not necessary, as solution data is sufficient to train the network to learn the discrete operators. A once-trained STENCIL-NET model can be used to predict solutions of the PDE on larger spatial domains and for longer times than it was trained for, hence addressing the problem of PDE-constrained extrapolation from data. To support this claim, we present numerical experiments on long-term forecasting of chaotic PDE solutions on coarse spatio-temporal grids. We also quantify the speed-up achieved by substituting base-line numerical methods with equation-free STENCIL-NET predictions on coarser grids with little compromise on accuracy.

Learning physically consistent mathematical models from data using group sparsity

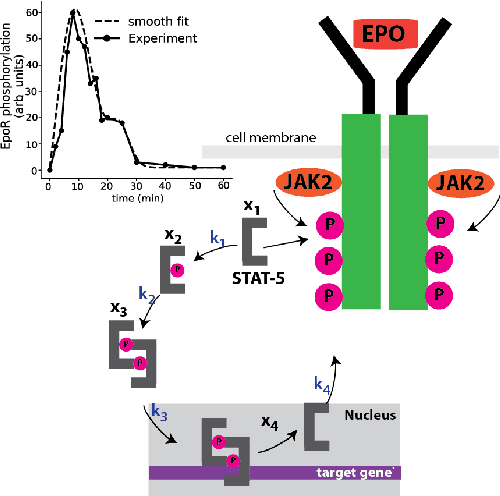
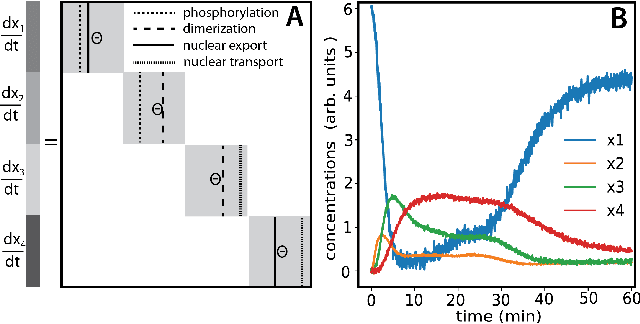
We propose a statistical learning framework based on group-sparse regression that can be used to 1) enforce conservation laws, 2) ensure model equivalence, and 3) guarantee symmetries when learning or inferring differential-equation models from measurement data. Directly learning $\textit{interpretable}$ mathematical models from data has emerged as a valuable modeling approach. However, in areas like biology, high noise levels, sensor-induced correlations, and strong inter-system variability can render data-driven models nonsensical or physically inconsistent without additional constraints on the model structure. Hence, it is important to leverage $\textit{prior}$ knowledge from physical principles to learn "biologically plausible and physically consistent" models rather than models that simply fit the data best. We present a novel group Iterative Hard Thresholding (gIHT) algorithm and use stability selection to infer physically consistent models with minimal parameter tuning. We show several applications from systems biology that demonstrate the benefits of enforcing $\textit{priors}$ in data-driven modeling.

c-lasso -- a Python package for constrained sparse and robust regression and classification

We introduce c-lasso, a Python package that enables sparse and robust linear regression and classification with linear equality constraints. The underlying statistical forward model is assumed to be of the following form: \[ y = X \beta + \sigma \epsilon \qquad \textrm{subject to} \qquad C\beta=0 \] Here, $X \in \mathbb{R}^{n\times d}$is a given design matrix and the vector $y \in \mathbb{R}^{n}$ is a continuous or binary response vector. The matrix $C$ is a general constraint matrix. The vector $\beta \in \mathbb{R}^{d}$ contains the unknown coefficients and $\sigma$ an unknown scale. Prominent use cases are (sparse) log-contrast regression with compositional data $X$, requiring the constraint $1_d^T \beta = 0$ (Aitchion and Bacon-Shone 1984) and the Generalized Lasso which is a special case of the described problem (see, e.g, (James, Paulson, and Rusmevichientong 2020), Example 3). The c-lasso package provides estimators for inferring unknown coefficients and scale (i.e., perspective M-estimators (Combettes and M\"uller 2020a)) of the form \[ \min_{\beta \in \mathbb{R}^d, \sigma \in \mathbb{R}_{0}} f\left(X\beta - y,{\sigma} \right) + \lambda \left\lVert \beta\right\rVert_1 \qquad \textrm{subject to} \qquad C\beta = 0 \] for several convex loss functions $f(\cdot,\cdot)$. This includes the constrained Lasso, the constrained scaled Lasso, and sparse Huber M-estimators with linear equality constraints.

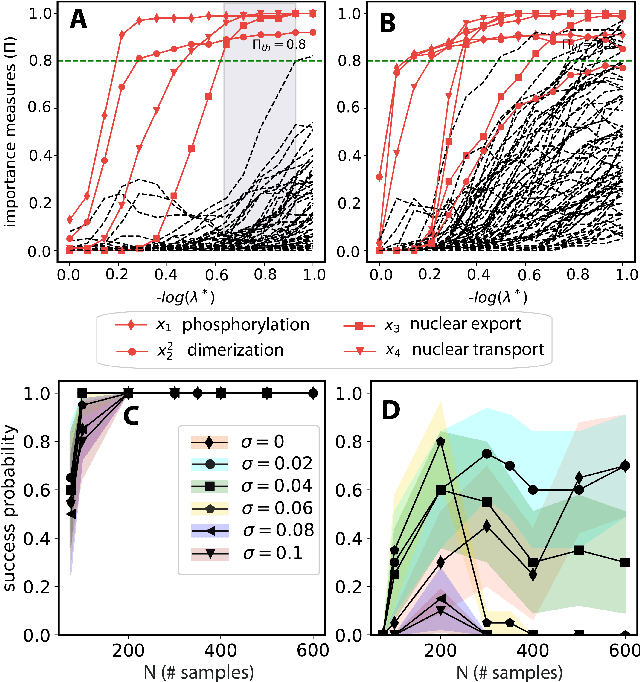
Stability selection enables robust learning of partial differential equations from limited noisy data

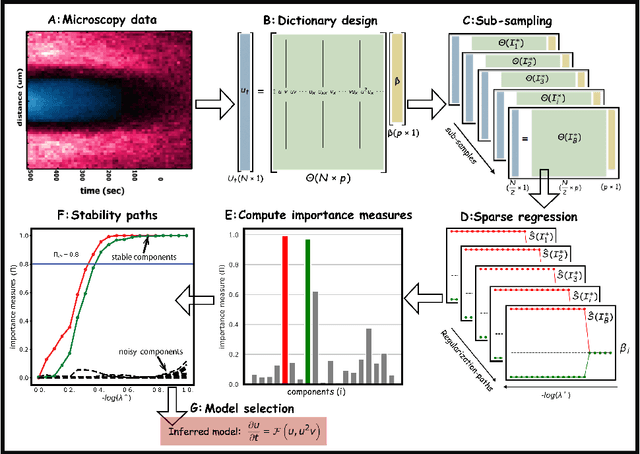
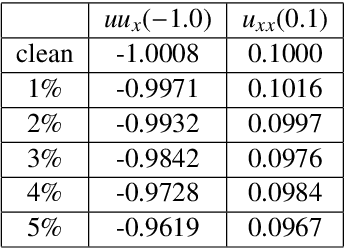
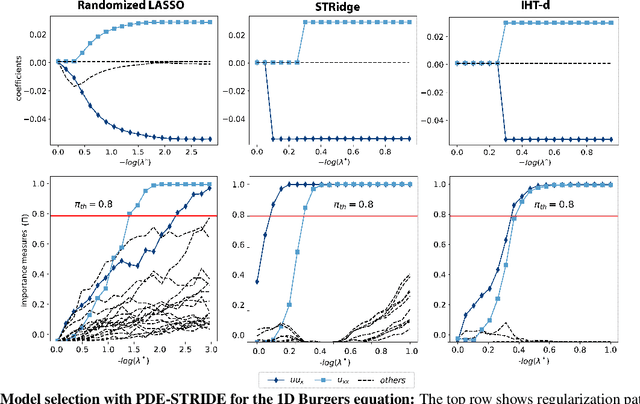
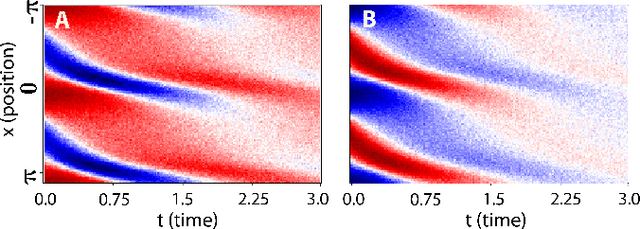
We present a statistical learning framework for robust identification of partial differential equations from noisy spatiotemporal data. Extending previous sparse regression approaches for inferring PDE models from simulated data, we address key issues that have thus far limited the application of these methods to noisy experimental data, namely their robustness against noise and the need for manual parameter tuning. We address both points by proposing a stability-based model selection scheme to determine the level of regularization required for reproducible recovery of the underlying PDE. This avoids manual parameter tuning and provides a principled way to improve the method's robustness against noise in the data. Our stability selection approach, termed PDE-STRIDE, can be combined with any sparsity-promoting penalized regression model and provides an interpretable criterion for model component importance. We show that in particular the combination of stability selection with the iterative hard-thresholding algorithm from compressed sensing provides a fast, parameter-free, and robust computational framework for PDE inference that outperforms previous algorithmic approaches with respect to recovery accuracy, amount of data required, and robustness to noise. We illustrate the performance of our approach on a wide range of noise-corrupted simulated benchmark problems, including 1D Burgers, 2D vorticity-transport, and 3D reaction-diffusion problems. We demonstrate the practical applicability of our method on real-world data by considering a purely data-driven re-evaluation of the advective triggering hypothesis for an embryonic polarization system in C.~elegans. Using fluorescence microscopy images of C.~elegans zygotes as input data, our framework is able to recover the PDE model for the regulatory reaction-diffusion-flow network of the associated proteins.