Learning locally dominant force balances in active particle systems

We use a combination of unsupervised clustering and sparsity-promoting inference algorithms to learn locally dominant force balances that explain macroscopic pattern formation in self-organized active particle systems. The self-organized emergence of macroscopic patterns from microscopic interactions between self-propelled particles can be widely observed nature. Although hydrodynamic theories help us better understand the physical basis of this phenomenon, identifying a sufficient set of local interactions that shape, regulate, and sustain self-organized structures in active particle systems remains challenging. We investigate a classic hydrodynamic model of self-propelled particles that produces a wide variety of patterns, like asters and moving density bands. Our data-driven analysis shows that propagating bands are formed by local alignment interactions driven by density gradients, while steady-state asters are shaped by a mechanism of splay-induced negative compressibility arising from strong particle interactions. Our method also reveals analogous physical principles of pattern formation in a system where the speed of the particle is influenced by local density. This demonstrates the ability of our method to reveal physical commonalities across models. The physical mechanisms inferred from the data are in excellent agreement with analytical scaling arguments and experimental observations.

Inverse-Dirichlet Weighting Enables Reliable Training of Physics Informed Neural Networks

We characterize and remedy a failure mode that may arise from multi-scale dynamics with scale imbalances during training of deep neural networks, such as Physics Informed Neural Networks (PINNs). PINNs are popular machine-learning templates that allow for seamless integration of physical equation models with data. Their training amounts to solving an optimization problem over a weighted sum of data-fidelity and equation-fidelity objectives. Conflicts between objectives can arise from scale imbalances, heteroscedasticity in the data, stiffness of the physical equation, or from catastrophic interference during sequential training. We explain the training pathology arising from this and propose a simple yet effective inverse-Dirichlet weighting strategy to alleviate the issue. We compare with Sobolev training of neural networks, providing the baseline of analytically $\boldsymbol{\epsilon}$-optimal training. We demonstrate the effectiveness of inverse-Dirichlet weighting in various applications, including a multi-scale model of active turbulence, where we show orders of magnitude improvement in accuracy and convergence over conventional PINN training. For inverse modeling using sequential training, we find that inverse-Dirichlet weighting protects a PINN against catastrophic forgetting.

STENCIL-NET: Data-driven solution-adaptive discretization of partial differential equations

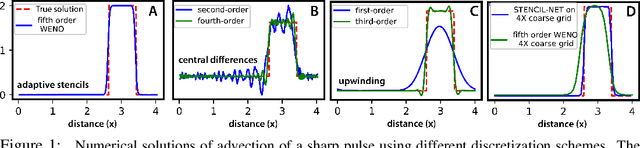
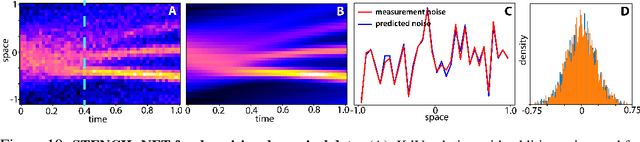
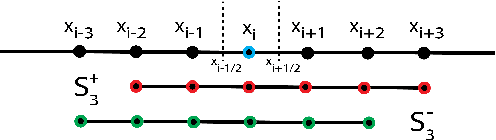
Numerical methods for approximately solving partial differential equations (PDE) are at the core of scientific computing. Often, this requires high-resolution or adaptive discretization grids to capture relevant spatio-temporal features in the PDE solution, e.g., in applications like turbulence, combustion, and shock propagation. Numerical approximation also requires knowing the PDE in order to construct problem-specific discretizations. Systematically deriving such solution-adaptive discrete operators, however, is a current challenge. Here we present STENCIL-NET, an artificial neural network architecture for data-driven learning of problem- and resolution-specific local discretizations of nonlinear PDEs. STENCIL-NET achieves numerically stable discretization of the operators in an unknown nonlinear PDE by spatially and temporally adaptive parametric pooling on regular Cartesian grids, and by incorporating knowledge about discrete time integration. Knowing the actual PDE is not necessary, as solution data is sufficient to train the network to learn the discrete operators. A once-trained STENCIL-NET model can be used to predict solutions of the PDE on larger spatial domains and for longer times than it was trained for, hence addressing the problem of PDE-constrained extrapolation from data. To support this claim, we present numerical experiments on long-term forecasting of chaotic PDE solutions on coarse spatio-temporal grids. We also quantify the speed-up achieved by substituting base-line numerical methods with equation-free STENCIL-NET predictions on coarser grids with little compromise on accuracy.