Bevan L. Cheeseman
Parallel Discrete Convolutions on Adaptive Particle Representations of Images
Dec 07, 2021



Abstract:We present data structures and algorithms for native implementations of discrete convolution operators over Adaptive Particle Representations (APR) of images on parallel computer architectures. The APR is a content-adaptive image representation that locally adapts the sampling resolution to the image signal. It has been developed as an alternative to pixel representations for large, sparse images as they typically occur in fluorescence microscopy. It has been shown to reduce the memory and runtime costs of storing, visualizing, and processing such images. This, however, requires that image processing natively operates on APRs, without intermediately reverting to pixels. Designing efficient and scalable APR-native image processing primitives, however, is complicated by the APR's irregular memory structure. Here, we provide the algorithmic building blocks required to efficiently and natively process APR images using a wide range of algorithms that can be formulated in terms of discrete convolutions. We show that APR convolution naturally leads to scale-adaptive algorithms that efficiently parallelize on multi-core CPU and GPU architectures. We quantify the speedups in comparison to pixel-based algorithms and convolutions on evenly sampled data. We achieve pixel-equivalent throughputs of up to 1 TB/s on a single Nvidia GeForce RTX 2080 gaming GPU, requiring up to two orders of magnitude less memory than a pixel-based implementation.
STENCIL-NET: Data-driven solution-adaptive discretization of partial differential equations
Jan 18, 2021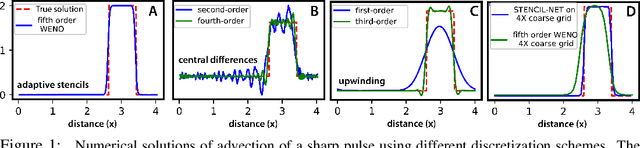
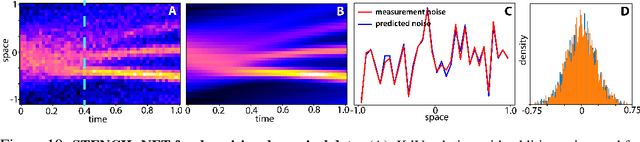
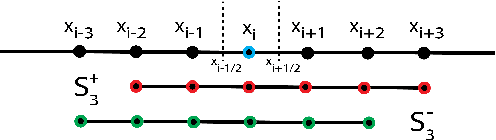

Abstract:Numerical methods for approximately solving partial differential equations (PDE) are at the core of scientific computing. Often, this requires high-resolution or adaptive discretization grids to capture relevant spatio-temporal features in the PDE solution, e.g., in applications like turbulence, combustion, and shock propagation. Numerical approximation also requires knowing the PDE in order to construct problem-specific discretizations. Systematically deriving such solution-adaptive discrete operators, however, is a current challenge. Here we present STENCIL-NET, an artificial neural network architecture for data-driven learning of problem- and resolution-specific local discretizations of nonlinear PDEs. STENCIL-NET achieves numerically stable discretization of the operators in an unknown nonlinear PDE by spatially and temporally adaptive parametric pooling on regular Cartesian grids, and by incorporating knowledge about discrete time integration. Knowing the actual PDE is not necessary, as solution data is sufficient to train the network to learn the discrete operators. A once-trained STENCIL-NET model can be used to predict solutions of the PDE on larger spatial domains and for longer times than it was trained for, hence addressing the problem of PDE-constrained extrapolation from data. To support this claim, we present numerical experiments on long-term forecasting of chaotic PDE solutions on coarse spatio-temporal grids. We also quantify the speed-up achieved by substituting base-line numerical methods with equation-free STENCIL-NET predictions on coarser grids with little compromise on accuracy.
Learning physically consistent mathematical models from data using group sparsity
Dec 11, 2020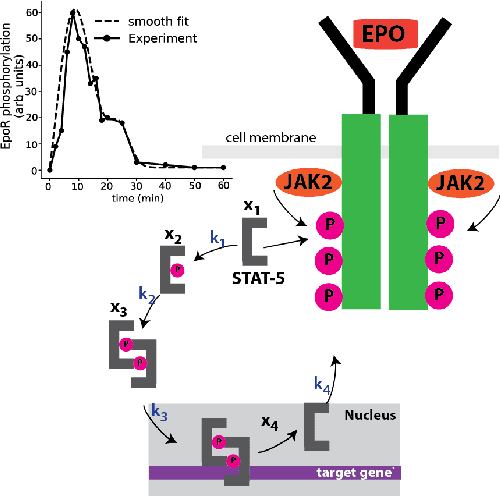
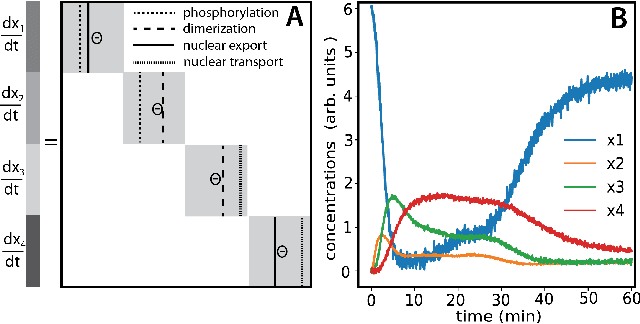
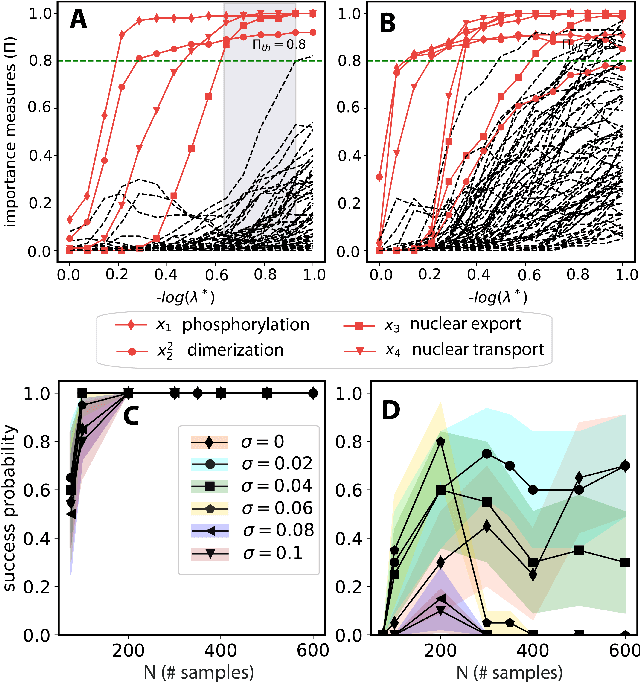
Abstract:We propose a statistical learning framework based on group-sparse regression that can be used to 1) enforce conservation laws, 2) ensure model equivalence, and 3) guarantee symmetries when learning or inferring differential-equation models from measurement data. Directly learning $\textit{interpretable}$ mathematical models from data has emerged as a valuable modeling approach. However, in areas like biology, high noise levels, sensor-induced correlations, and strong inter-system variability can render data-driven models nonsensical or physically inconsistent without additional constraints on the model structure. Hence, it is important to leverage $\textit{prior}$ knowledge from physical principles to learn "biologically plausible and physically consistent" models rather than models that simply fit the data best. We present a novel group Iterative Hard Thresholding (gIHT) algorithm and use stability selection to infer physically consistent models with minimal parameter tuning. We show several applications from systems biology that demonstrate the benefits of enforcing $\textit{priors}$ in data-driven modeling.
Stability selection enables robust learning of partial differential equations from limited noisy data
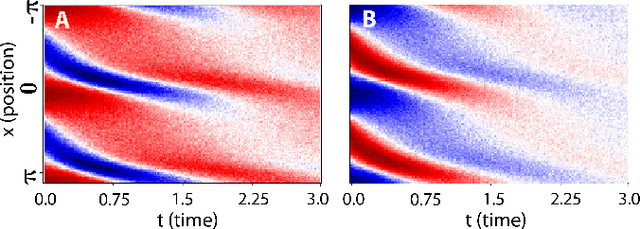
Jul 17, 2019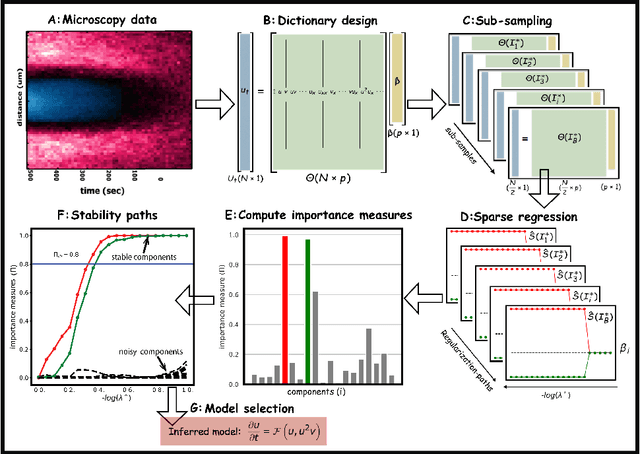
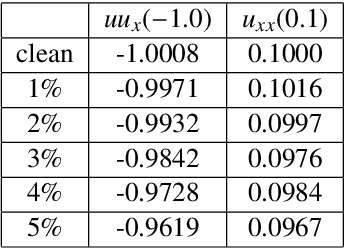
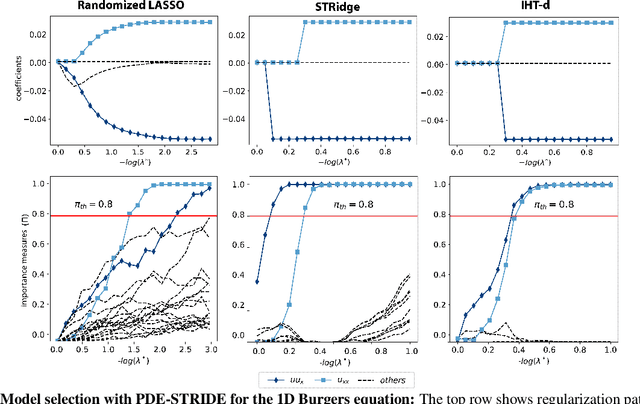

Abstract:We present a statistical learning framework for robust identification of partial differential equations from noisy spatiotemporal data. Extending previous sparse regression approaches for inferring PDE models from simulated data, we address key issues that have thus far limited the application of these methods to noisy experimental data, namely their robustness against noise and the need for manual parameter tuning. We address both points by proposing a stability-based model selection scheme to determine the level of regularization required for reproducible recovery of the underlying PDE. This avoids manual parameter tuning and provides a principled way to improve the method's robustness against noise in the data. Our stability selection approach, termed PDE-STRIDE, can be combined with any sparsity-promoting penalized regression model and provides an interpretable criterion for model component importance. We show that in particular the combination of stability selection with the iterative hard-thresholding algorithm from compressed sensing provides a fast, parameter-free, and robust computational framework for PDE inference that outperforms previous algorithmic approaches with respect to recovery accuracy, amount of data required, and robustness to noise. We illustrate the performance of our approach on a wide range of noise-corrupted simulated benchmark problems, including 1D Burgers, 2D vorticity-transport, and 3D reaction-diffusion problems. We demonstrate the practical applicability of our method on real-world data by considering a purely data-driven re-evaluation of the advective triggering hypothesis for an embryonic polarization system in C.~elegans. Using fluorescence microscopy images of C.~elegans zygotes as input data, our framework is able to recover the PDE model for the regulatory reaction-diffusion-flow network of the associated proteins.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge