Learning physically consistent mathematical models from data using group sparsity
Paper and Code
Dec 11, 2020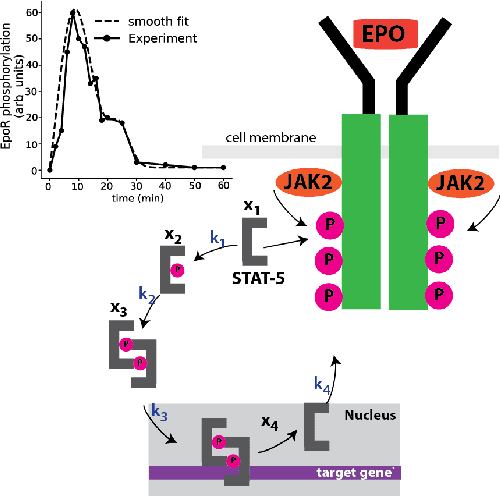
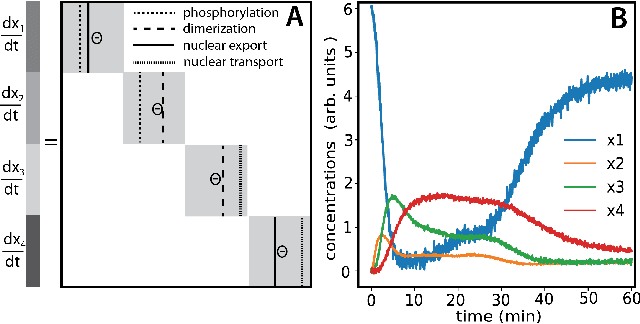
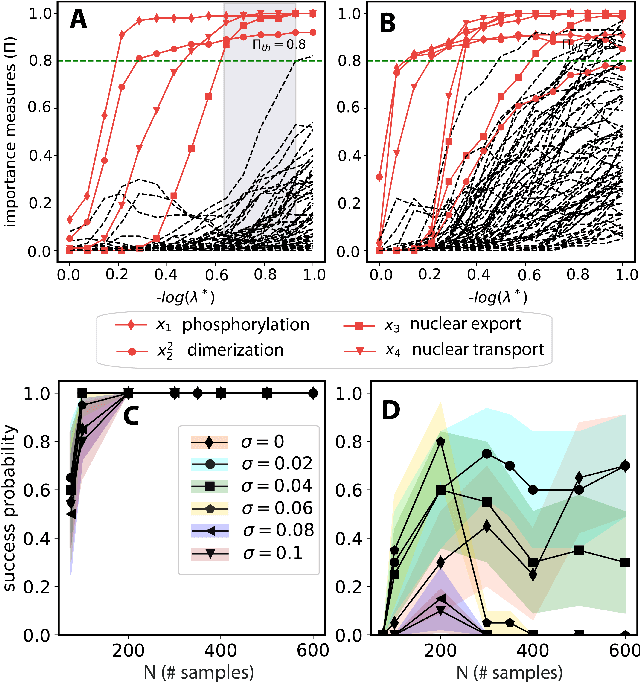
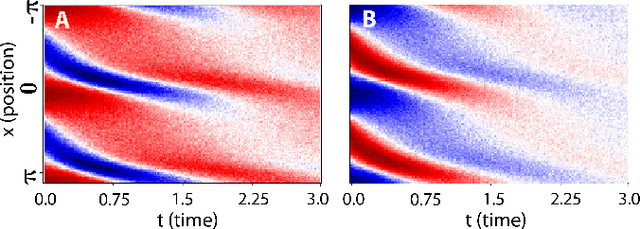
We propose a statistical learning framework based on group-sparse regression that can be used to 1) enforce conservation laws, 2) ensure model equivalence, and 3) guarantee symmetries when learning or inferring differential-equation models from measurement data. Directly learning $\textit{interpretable}$ mathematical models from data has emerged as a valuable modeling approach. However, in areas like biology, high noise levels, sensor-induced correlations, and strong inter-system variability can render data-driven models nonsensical or physically inconsistent without additional constraints on the model structure. Hence, it is important to leverage $\textit{prior}$ knowledge from physical principles to learn "biologically plausible and physically consistent" models rather than models that simply fit the data best. We present a novel group Iterative Hard Thresholding (gIHT) algorithm and use stability selection to infer physically consistent models with minimal parameter tuning. We show several applications from systems biology that demonstrate the benefits of enforcing $\textit{priors}$ in data-driven modeling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge