STENCIL-NET: Data-driven solution-adaptive discretization of partial differential equations
Paper and Code
Jan 18, 2021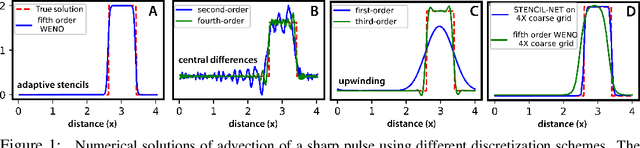
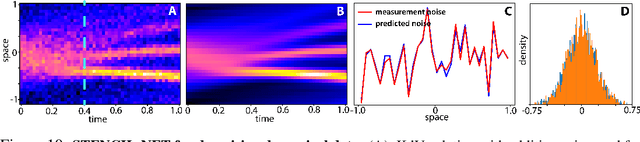
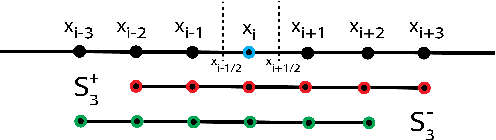

Numerical methods for approximately solving partial differential equations (PDE) are at the core of scientific computing. Often, this requires high-resolution or adaptive discretization grids to capture relevant spatio-temporal features in the PDE solution, e.g., in applications like turbulence, combustion, and shock propagation. Numerical approximation also requires knowing the PDE in order to construct problem-specific discretizations. Systematically deriving such solution-adaptive discrete operators, however, is a current challenge. Here we present STENCIL-NET, an artificial neural network architecture for data-driven learning of problem- and resolution-specific local discretizations of nonlinear PDEs. STENCIL-NET achieves numerically stable discretization of the operators in an unknown nonlinear PDE by spatially and temporally adaptive parametric pooling on regular Cartesian grids, and by incorporating knowledge about discrete time integration. Knowing the actual PDE is not necessary, as solution data is sufficient to train the network to learn the discrete operators. A once-trained STENCIL-NET model can be used to predict solutions of the PDE on larger spatial domains and for longer times than it was trained for, hence addressing the problem of PDE-constrained extrapolation from data. To support this claim, we present numerical experiments on long-term forecasting of chaotic PDE solutions on coarse spatio-temporal grids. We also quantify the speed-up achieved by substituting base-line numerical methods with equation-free STENCIL-NET predictions on coarser grids with little compromise on accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge