How Inverse Conditional Flows Can Serve as a Substitute for Distributional Regression

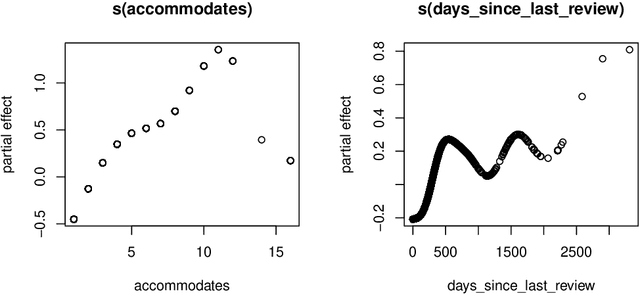
Neural network representations of simple models, such as linear regression, are being studied increasingly to better understand the underlying principles of deep learning algorithms. However, neural representations of distributional regression models, such as the Cox model, have received little attention so far. We close this gap by proposing a framework for distributional regression using inverse flow transformations (DRIFT), which includes neural representations of the aforementioned models. We empirically demonstrate that the neural representations of models in DRIFT can serve as a substitute for their classical statistical counterparts in several applications involving continuous, ordered, time-series, and survival outcomes. We confirm that models in DRIFT empirically match the performance of several statistical methods in terms of estimation of partial effects, prediction, and aleatoric uncertainty quantification. DRIFT covers both interpretable statistical models and flexible neural networks opening up new avenues in both statistical modeling and deep learning.

Generalizing Orthogonalization for Models with Non-linearities

The complexity of black-box algorithms can lead to various challenges, including the introduction of biases. These biases present immediate risks in the algorithms' application. It was, for instance, shown that neural networks can deduce racial information solely from a patient's X-ray scan, a task beyond the capability of medical experts. If this fact is not known to the medical expert, automatic decision-making based on this algorithm could lead to prescribing a treatment (purely) based on racial information. While current methodologies allow for the "orthogonalization" or "normalization" of neural networks with respect to such information, existing approaches are grounded in linear models. Our paper advances the discourse by introducing corrections for non-linearities such as ReLU activations. Our approach also encompasses scalar and tensor-valued predictions, facilitating its integration into neural network architectures. Through extensive experiments, we validate our method's effectiveness in safeguarding sensitive data in generalized linear models, normalizing convolutional neural networks for metadata, and rectifying pre-existing embeddings for undesired attributes.

Smoothing the Edges: A General Framework for Smooth Optimization in Sparse Regularization using Hadamard Overparametrization

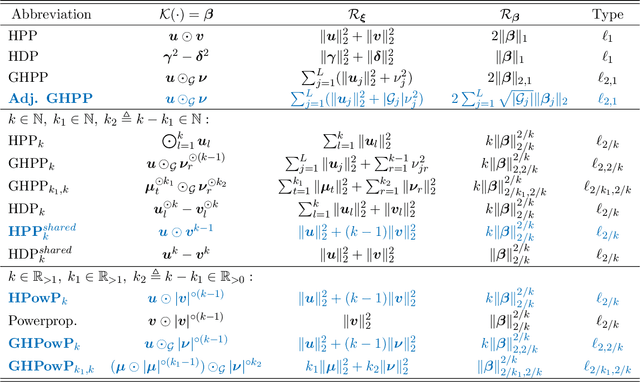
This paper introduces a smooth method for (structured) sparsity in $\ell_q$ and $\ell_{p,q}$ regularized optimization problems. Optimization of these non-smooth and possibly non-convex problems typically relies on specialized procedures. In contrast, our general framework is compatible with prevalent first-order optimization methods like Stochastic Gradient Descent and accelerated variants without any required modifications. This is accomplished through a smooth optimization transfer, comprising an overparametrization of selected model parameters using Hadamard products and a change of penalties. In the overparametrized problem, smooth and convex $\ell_2$ regularization of the surrogate parameters induces non-smooth and non-convex $\ell_q$ or $\ell_{p,q}$ regularization in the original parametrization. We show that our approach yields not only matching global minima but also equivalent local minima. This is particularly useful in non-convex sparse regularization, where finding global minima is NP-hard and local minima are known to generalize well. We provide a comprehensive overview consolidating various literature strands on sparsity-inducing parametrizations and propose meaningful extensions to existing approaches. The feasibility of our approach is evaluated through numerical experiments, which demonstrate that its performance is on par with or surpasses commonly used implementations of convex and non-convex regularization methods.

deepregression: a Flexible Neural Network Framework for Semi-Structured Deep Distributional Regression

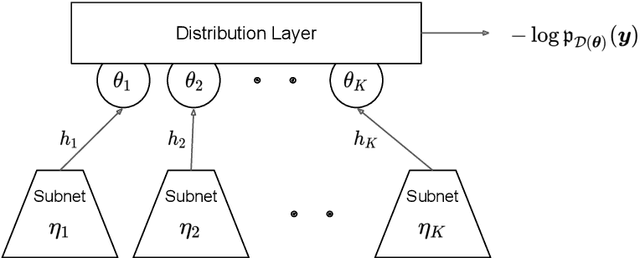
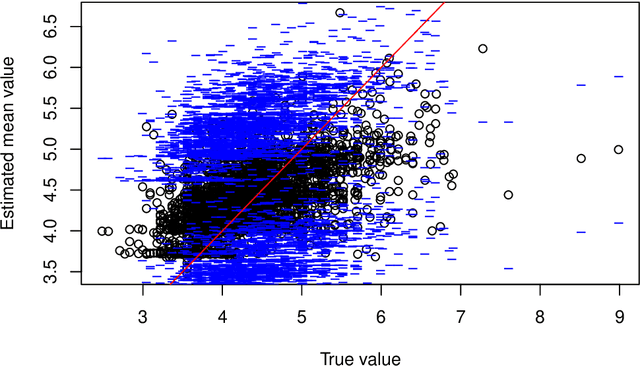
This paper describes the implementation of semi-structured deep distributional regression, a flexible framework to learn distributions based on a combination of additive regression models and deep neural networks. deepregression is implemented in both R and Python, using the deep learning libraries TensorFlow and PyTorch, respectively. The implementation consists of (1) a modular neural network building system for the combination of various statistical and deep learning approaches, (2) an orthogonalization cell to allow for an interpretable combination of different subnetworks as well as (3) pre-processing steps necessary to initialize such models. The software package allows to define models in a user-friendly manner using distribution definitions via a formula environment that is inspired by classical statistical model frameworks such as mgcv. The packages' modular design and functionality provides a unique resource for rapid and reproducible prototyping of complex statistical and deep learning models while simultaneously retaining the indispensable interpretability of classical statistical models.

A Unifying Network Architecture for Semi-Structured Deep Distributional Learning

We propose a unifying network architecture for deep distributional learning in which entire distributions can be learned in a general framework of interpretable regression models and deep neural networks. Previous approaches that try to combine advanced statistical models and deep neural networks embed the neural network part as a predictor in an additive regression model. In contrast, our approach estimates the statistical model part within a unifying neural network by projecting the deep learning model part into the orthogonal complement of the regression model predictor. This facilitates both estimation and interpretability in high-dimensional settings. We identify appropriate default penalties that can also be treated as prior distribution assumptions in the Bayesian version of our network architecture. We consider several use-cases in experiments with synthetic data and real world applications to demonstrate the full efficacy of our approach.