Inferring biological processes with intrinsic noise from cross-sectional data
Paper and Code
Oct 10, 2024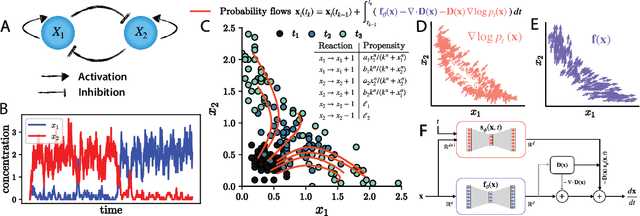
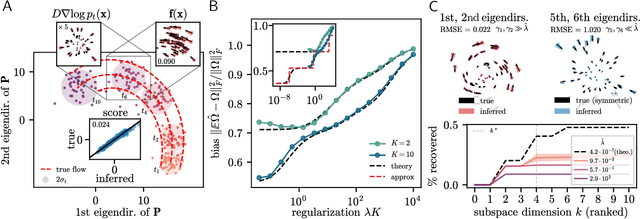
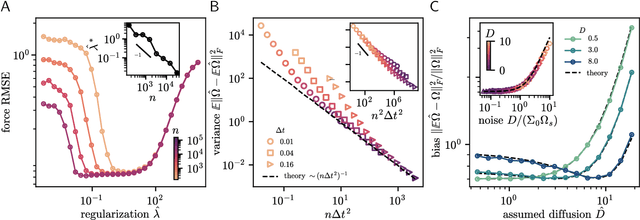
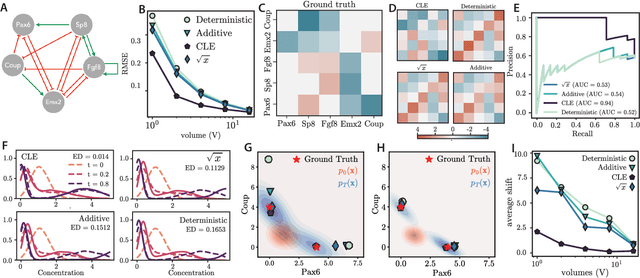
Inferring dynamical models from data continues to be a significant challenge in computational biology, especially given the stochastic nature of many biological processes. We explore a common scenario in omics, where statistically independent cross-sectional samples are available at a few time points, and the goal is to infer the underlying diffusion process that generated the data. Existing inference approaches often simplify or ignore noise intrinsic to the system, compromising accuracy for the sake of optimization ease. We circumvent this compromise by inferring the phase-space probability flow that shares the same time-dependent marginal distributions as the underlying stochastic process. Our approach, probability flow inference (PFI), disentangles force from intrinsic stochasticity while retaining the algorithmic ease of ODE inference. Analytically, we prove that for Ornstein-Uhlenbeck processes the regularized PFI formalism yields a unique solution in the limit of well-sampled distributions. In practical applications, we show that PFI enables accurate parameter and force estimation in high-dimensional stochastic reaction networks, and that it allows inference of cell differentiation dynamics with molecular noise, outperforming state-of-the-art approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge