Inferring biological processes with intrinsic noise from cross-sectional data

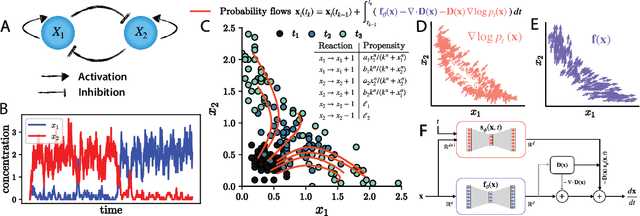
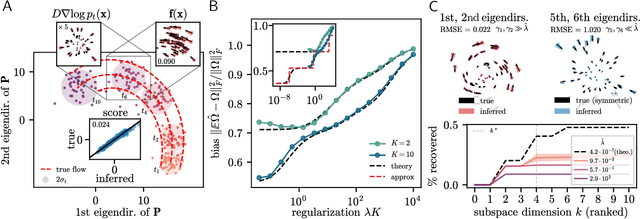
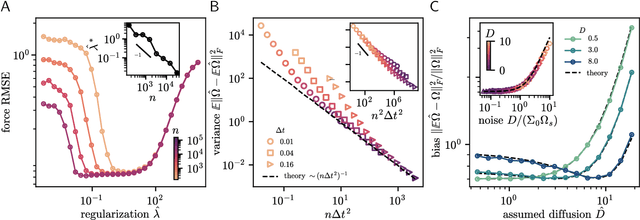
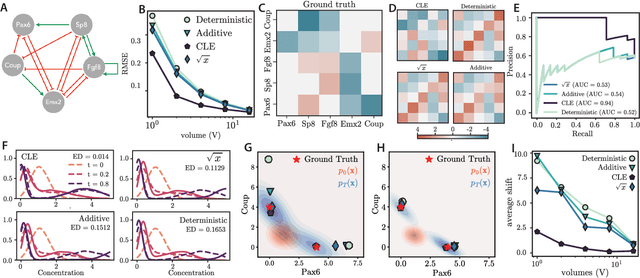
Inferring dynamical models from data continues to be a significant challenge in computational biology, especially given the stochastic nature of many biological processes. We explore a common scenario in omics, where statistically independent cross-sectional samples are available at a few time points, and the goal is to infer the underlying diffusion process that generated the data. Existing inference approaches often simplify or ignore noise intrinsic to the system, compromising accuracy for the sake of optimization ease. We circumvent this compromise by inferring the phase-space probability flow that shares the same time-dependent marginal distributions as the underlying stochastic process. Our approach, probability flow inference (PFI), disentangles force from intrinsic stochasticity while retaining the algorithmic ease of ODE inference. Analytically, we prove that for Ornstein-Uhlenbeck processes the regularized PFI formalism yields a unique solution in the limit of well-sampled distributions. In practical applications, we show that PFI enables accurate parameter and force estimation in high-dimensional stochastic reaction networks, and that it allows inference of cell differentiation dynamics with molecular noise, outperforming state-of-the-art approaches.

Stochastic force inference via density estimation

Inferring dynamical models from low-resolution temporal data continues to be a significant challenge in biophysics, especially within transcriptomics, where separating molecular programs from noise remains an important open problem. We explore a common scenario in which we have access to an adequate amount of cross-sectional samples at a few time-points, and assume that our samples are generated from a latent diffusion process. We propose an approach that relies on the probability flow associated with an underlying diffusion process to infer an autonomous, nonlinear force field interpolating between the distributions. Given a prior on the noise model, we employ score-matching to differentiate the force field from the intrinsic noise. Using relevant biophysical examples, we demonstrate that our approach can extract non-conservative forces from non-stationary data, that it learns equilibrium dynamics when applied to steady-state data, and that it can do so with both additive and multiplicative noise models.

The Connection between Discrete- and Continuous-Time Descriptions of Gaussian Continuous Processes

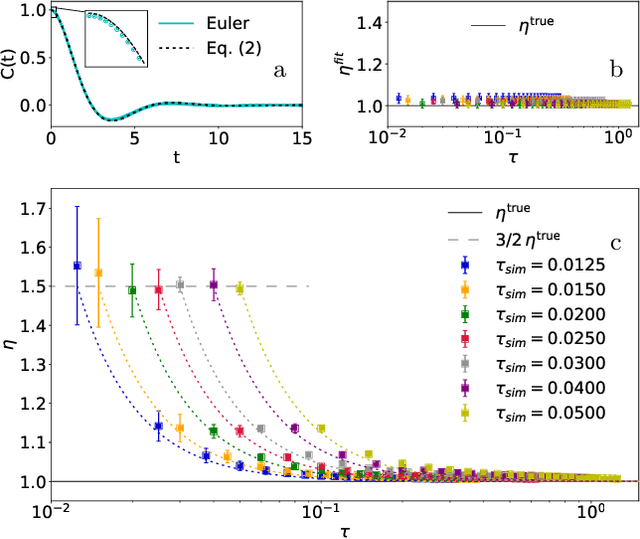
Learning the continuous equations of motion from discrete observations is a common task in all areas of physics. However, not any discretization of a Gaussian continuous-time stochastic process can be adopted in parametric inference. We show that discretizations yielding consistent estimators have the property of `invariance under coarse-graining', and correspond to fixed points of a renormalization group map on the space of autoregressive moving average (ARMA) models (for linear processes). This result explains why combining differencing schemes for derivatives reconstruction and local-in-time inference approaches does not work for time series analysis of second or higher order stochastic differential equations, even if the corresponding integration schemes may be acceptably good for numerical simulations.