Retraining with Predicted Hard Labels Provably Increases Model Accuracy

The performance of a model trained with \textit{noisy labels} is often improved by simply \textit{retraining} the model with its own predicted \textit{hard} labels (i.e., $1$/$0$ labels). Yet, a detailed theoretical characterization of this phenomenon is lacking. In this paper, we theoretically analyze retraining in a linearly separable setting with randomly corrupted labels given to us and prove that retraining can improve the population accuracy obtained by initially training with the given (noisy) labels. To the best of our knowledge, this is the first such theoretical result. Retraining finds application in improving training with label differential privacy (DP) which involves training with noisy labels. We empirically show that retraining selectively on the samples for which the predicted label matches the given label significantly improves label DP training at \textit{no extra privacy cost}; we call this \textit{consensus-based retraining}. For e.g., when training ResNet-18 on CIFAR-100 with $\epsilon=3$ label DP, we obtain $6.4\%$ improvement in accuracy with consensus-based retraining.

Towards Quantifying the Preconditioning Effect of Adam

There is a notable dearth of results characterizing the preconditioning effect of Adam and showing how it may alleviate the curse of ill-conditioning -- an issue plaguing gradient descent (GD). In this work, we perform a detailed analysis of Adam's preconditioning effect for quadratic functions and quantify to what extent Adam can mitigate the dependence on the condition number of the Hessian. Our key finding is that Adam can suffer less from the condition number but at the expense of suffering a dimension-dependent quantity. Specifically, for a $d$-dimensional quadratic with a diagonal Hessian having condition number $\kappa$, we show that the effective condition number-like quantity controlling the iteration complexity of Adam without momentum is $\mathcal{O}(\min(d, \kappa))$. For a diagonally dominant Hessian, we obtain a bound of $\mathcal{O}(\min(d \sqrt{d \kappa}, \kappa))$ for the corresponding quantity. Thus, when $d < \mathcal{O}(\kappa^p)$ where $p = 1$ for a diagonal Hessian and $p = 1/3$ for a diagonally dominant Hessian, Adam can outperform GD (which has an $\mathcal{O}(\kappa)$ dependence). On the negative side, our results suggest that Adam can be worse than GD for a sufficiently non-diagonal Hessian even if $d \ll \mathcal{O}(\kappa^{1/3})$; we corroborate this with empirical evidence. Finally, we extend our analysis to functions satisfying per-coordinate Lipschitz smoothness and a modified version of the Polyak-\L ojasiewicz condition.

Understanding the Training Speedup from Sampling with Approximate Losses

It is well known that selecting samples with large losses/gradients can significantly reduce the number of training steps. However, the selection overhead is often too high to yield any meaningful gains in terms of overall training time. In this work, we focus on the greedy approach of selecting samples with large \textit{approximate losses} instead of exact losses in order to reduce the selection overhead. For smooth convex losses, we show that such a greedy strategy can converge to a constant factor of the minimum value of the average loss in fewer iterations than the standard approach of random selection. We also theoretically quantify the effect of the approximation level. We then develop SIFT which uses early exiting to obtain approximate losses with an intermediate layer's representations for sample selection. We evaluate SIFT on the task of training a 110M parameter 12-layer BERT base model and show significant gains (in terms of training hours and number of backpropagation steps) without any optimized implementation over vanilla training. For e.g., to reach 64% validation accuracy, SIFT with exit at the first layer takes ~43 hours compared to ~57 hours of vanilla training.

Understanding Self-Distillation in the Presence of Label Noise

Self-distillation (SD) is the process of first training a \enquote{teacher} model and then using its predictions to train a \enquote{student} model with the \textit{same} architecture. Specifically, the student's objective function is $\big(\xi*\ell(\text{teacher's predictions}, \text{ student's predictions}) + (1-\xi)*\ell(\text{given labels}, \text{ student's predictions})\big)$, where $\ell$ is some loss function and $\xi$ is some parameter $\in [0,1]$. Empirically, SD has been observed to provide performance gains in several settings. In this paper, we theoretically characterize the effect of SD in two supervised learning problems with \textit{noisy labels}. We first analyze SD for regularized linear regression and show that in the high label noise regime, the optimal value of $\xi$ that minimizes the expected error in estimating the ground truth parameter is surprisingly greater than 1. Empirically, we show that $\xi > 1$ works better than $\xi \leq 1$ even with the cross-entropy loss for several classification datasets when 50\% or 30\% of the labels are corrupted. Further, we quantify when optimal SD is better than optimal regularization. Next, we analyze SD in the case of logistic regression for binary classification with random label corruption and quantify the range of label corruption in which the student outperforms the teacher in terms of accuracy. To our knowledge, this is the first result of its kind for the cross-entropy loss.

Beyond Uniform Lipschitz Condition in Differentially Private Optimization

Most prior convergence results on differentially private stochastic gradient descent (DP-SGD) are derived under the simplistic assumption of uniform Lipschitzness, i.e., the per-sample gradients are uniformly bounded. This assumption is unrealistic in many problems, e.g., linear regression with Gaussian data. We relax uniform Lipschitzness by instead assuming that the per-sample gradients have \textit{sample-dependent} upper bounds, i.e., per-sample Lipschitz constants, which themselves may be unbounded. We derive new convergence results for DP-SGD on both convex and nonconvex functions when the per-sample Lipschitz constants have bounded moments. Furthermore, we provide principled guidance on choosing the clip norm in DP-SGD for convex settings satisfying our relaxed version of Lipschitzness, without making distributional assumptions on the Lipschitz constants. We verify the effectiveness of our recommendation via experiments on benchmarking datasets.

On the Unreasonable Effectiveness of Federated Averaging with Heterogeneous Data

Existing theory predicts that data heterogeneity will degrade the performance of the Federated Averaging (FedAvg) algorithm in federated learning. However, in practice, the simple FedAvg algorithm converges very well. This paper explains the seemingly unreasonable effectiveness of FedAvg that contradicts the previous theoretical predictions. We find that the key assumption of bounded gradient dissimilarity in previous theoretical analyses is too pessimistic to characterize data heterogeneity in practical applications. For a simple quadratic problem, we demonstrate there exist regimes where large gradient dissimilarity does not have any negative impact on the convergence of FedAvg. Motivated by this observation, we propose a new quantity, average drift at optimum, to measure the effects of data heterogeneity, and explicitly use it to present a new theoretical analysis of FedAvg. We show that the average drift at optimum is nearly zero across many real-world federated training tasks, whereas the gradient dissimilarity can be large. And our new analysis suggests FedAvg can have identical convergence rates in homogeneous and heterogeneous data settings, and hence, leads to better understanding of its empirical success.

DISCO : efficient unsupervised decoding for discrete natural language problems via convex relaxation

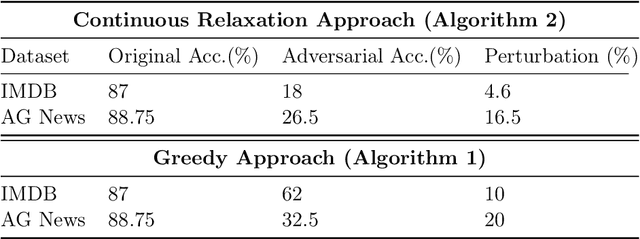
In this paper we study test time decoding; an ubiquitous step in almost all sequential text generation task spanning across a wide array of natural language processing (NLP) problems. Our main contribution is to develop a continuous relaxation framework for the combinatorial NP-hard decoding problem and propose Disco - an efficient algorithm based on standard first order gradient based. We provide tight analysis and show that our proposed algorithm linearly converges to within $\epsilon$ neighborhood of the optima. Finally, we perform preliminary experiments on the task of adversarial text generation and show superior performance of Disco over several popular decoding approaches.

DP-NormFedAvg: Normalizing Client Updates for Privacy-Preserving Federated Learning

In this paper, we focus on facilitating differentially private quantized communication between the clients and server in federated learning (FL). Towards this end, we propose to have the clients send a \textit{private quantized} version of only the \textit{unit vector} along the change in their local parameters to the server, \textit{completely throwing away the magnitude information}. We call this algorithm \texttt{DP-NormFedAvg} and show that it has the same order-wise convergence rate as \texttt{FedAvg} on smooth quasar-convex functions (an important class of non-convex functions for modeling optimization of deep neural networks), thereby establishing that discarding the magnitude information is not detrimental from an optimization point of view. We also introduce QTDL, a new differentially private quantization mechanism for unit-norm vectors, which we use in \texttt{DP-NormFedAvg}. QTDL employs \textit{discrete} noise having a Laplacian-like distribution on a \textit{finite support} to provide privacy. We show that under a growth-condition assumption on the per-sample client losses, the extra per-coordinate communication cost in each round incurred due to privacy by our method is $\mathcal{O}(1)$ with respect to the model dimension, which is an improvement over prior work. Finally, we show the efficacy of our proposed method with experiments on fully-connected neural networks trained on CIFAR-10 and Fashion-MNIST.

Improved Convergence Rates for Non-Convex Federated Learning with Compression

Federated learning is a new distributed learning paradigm that enables efficient training of emerging large-scale machine learning models. In this paper, we consider federated learning on non-convex objectives with compressed communication from the clients to the central server. We propose a novel first-order algorithm (\texttt{FedSTEPH2}) that employs compressed communication and achieves the optimal iteration complexity of $\mathcal{O}(1/\epsilon^{1.5})$ to reach an $\epsilon$-stationary point (i.e. $\mathbb{E}[\|\nabla f(\bm{x})\|^2] \leq \epsilon$) on smooth non-convex objectives. The proposed scheme is the first algorithm that attains the aforementioned optimal complexity with compressed communication and without using full client gradients at each communication round. The key idea of \texttt{FedSTEPH2} that enables attaining this optimal complexity is applying judicious momentum terms both in the local client updates and the global server update. As a prequel to \texttt{FedSTEPH2}, we propose \texttt{FedSTEPH} which involves a momentum term only in the local client updates. We establish that \texttt{FedSTEPH} enjoys improved convergence rates under various non-convex settings (such as the Polyak-\L{}ojasiewicz condition) and with fewer assumptions than prior work.

On the Benefits of Multiple Gossip Steps in Communication-Constrained Decentralized Optimization

In decentralized optimization, it is common algorithmic practice to have nodes interleave (local) gradient descent iterations with gossip (i.e. averaging over the network) steps. Motivated by the training of large-scale machine learning models, it is also increasingly common to require that messages be {\em lossy compressed} versions of the local parameters. In this paper, we show that, in such compressed decentralized optimization settings, there are benefits to having {\em multiple} gossip steps between subsequent gradient iterations, even when the cost of doing so is appropriately accounted for e.g. by means of reducing the precision of compressed information. In particular, we show that having $O(\log\frac{1}{\epsilon})$ gradient iterations {with constant step size} - and $O(\log\frac{1}{\epsilon})$ gossip steps between every pair of these iterations - enables convergence to within $\epsilon$ of the optimal value for smooth non-convex objectives satisfying Polyak-\L{}ojasiewicz condition. This result also holds for smooth strongly convex objectives. To our knowledge, this is the first work that derives convergence results for nonconvex optimization under arbitrary communication compression.