Weimin Wu
On Structured State-Space Duality
Oct 06, 2025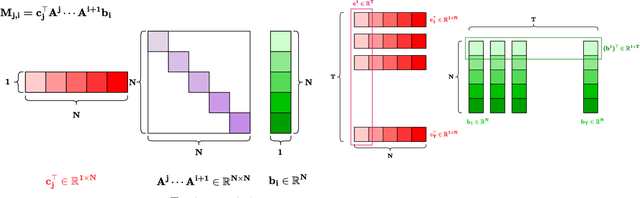
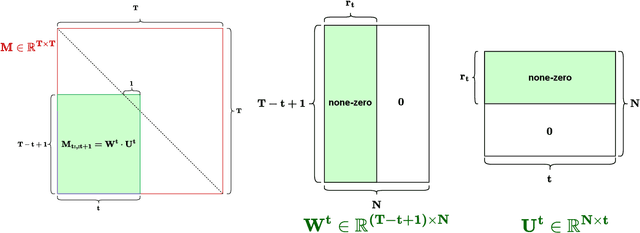
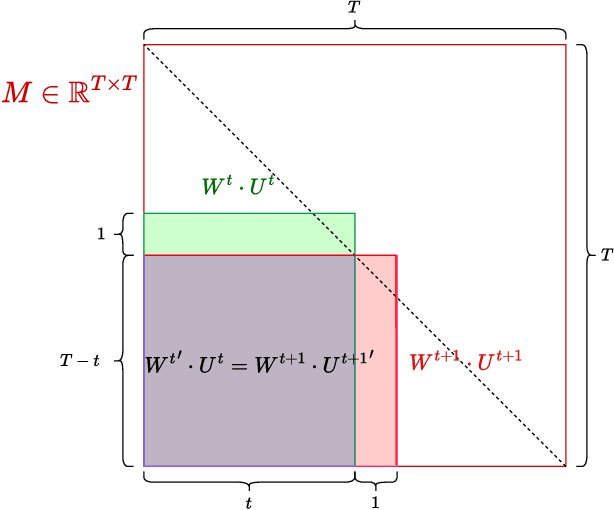
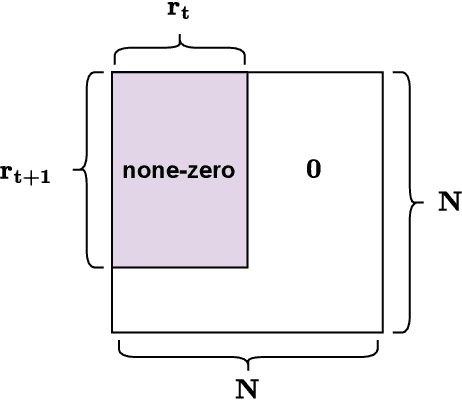
Abstract:Structured State-Space Duality (SSD) [Dao & Gu, ICML 2024] is an equivalence between a simple Structured State-Space Model (SSM) and a masked attention mechanism. In particular, a state-space model with a scalar-times-identity state matrix is equivalent to a masked self-attention with a $1$-semiseparable causal mask. Consequently, the same sequence transformation (model) has two algorithmic realizations: as a linear-time $O(T)$ recurrence or as a quadratic-time $O(T^2)$ attention. In this note, we formalize and generalize this duality: (i) we extend SSD from the scalar-identity case to general diagonal SSMs (diagonal state matrices); (ii) we show that these diagonal SSMs match the scalar case's training complexity lower bounds while supporting richer dynamics; (iii) we establish a necessary and sufficient condition under which an SSM is equivalent to $1$-semiseparable masked attention; and (iv) we show that such duality fails to extend to standard softmax attention due to rank explosion. Together, these results tighten bridge between recurrent SSMs and Transformers, and widen the design space for expressive yet efficient sequence models.
Petri Net Modeling and Deadlock-Free Scheduling of Attachable Heterogeneous AGV Systems
Aug 01, 2025
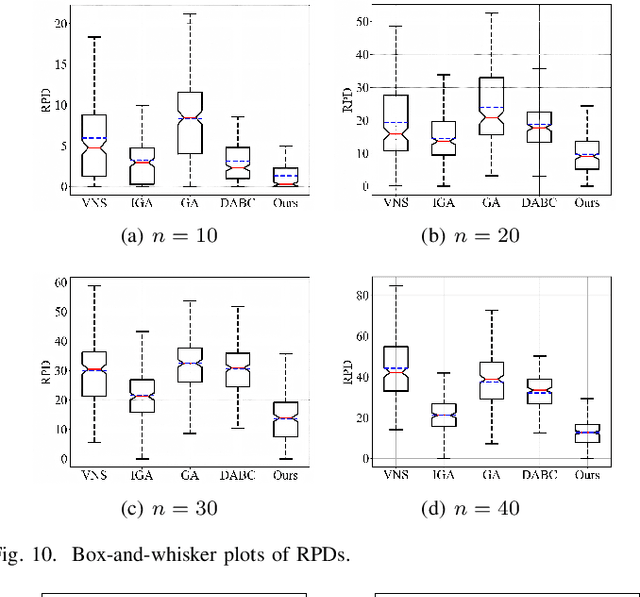
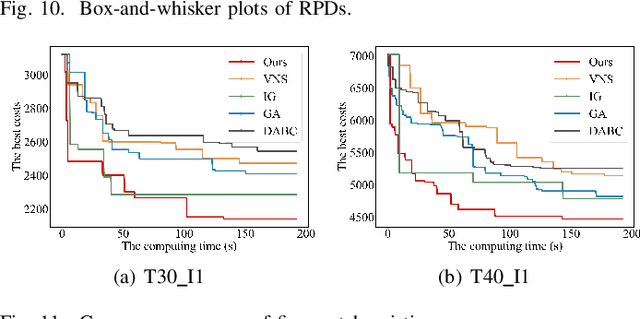
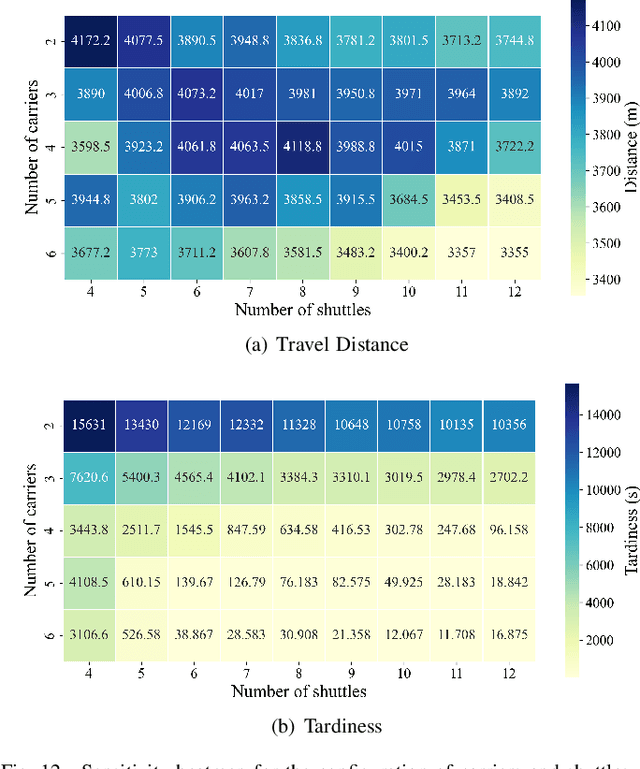
Abstract:The increasing demand for automation and flexibility drives the widespread adoption of heterogeneous automated guided vehicles (AGVs). This work intends to investigate a new scheduling problem in a material transportation system consisting of attachable heterogeneous AGVs, namely carriers and shuttles. They can flexibly attach to and detach from each other to cooperatively execute complex transportation tasks. While such collaboration enhances operational efficiency, the attachment-induced synchronization and interdependence render the scheduling coupled and susceptible to deadlock. To tackle this challenge, Petri nets are introduced to model AGV schedules, well describing the concurrent and sequential task execution and carrier-shuttle synchronization. Based on Petri net theory, a firing-driven decoding method is proposed, along with deadlock detection and prevention strategies to ensure deadlock-free schedules. Furthermore, a Petri net-based metaheuristic is developed in an adaptive large neighborhood search framework and incorporates an effective acceleration method to enhance computational efficiency. Finally, numerical experiments using real-world industrial data validate the effectiveness of the proposed algorithm against the scheduling policy applied in engineering practice, an exact solver, and four state-of-the-art metaheuristics. A sensitivity analysis is also conducted to provide managerial insights.
Universal Approximation with Softmax Attention
Apr 22, 2025Abstract:We prove that with linear transformations, both (i) two-layer self-attention and (ii) one-layer self-attention followed by a softmax function are universal approximators for continuous sequence-to-sequence functions on compact domains. Our main technique is a new interpolation-based method for analyzing attention's internal mechanism. This leads to our key insight: self-attention is able to approximate a generalized version of ReLU to arbitrary precision, and hence subsumes many known universal approximators. Building on these, we show that two-layer multi-head attention alone suffices as a sequence-to-sequence universal approximator. In contrast, prior works rely on feed-forward networks to establish universal approximation in Transformers. Furthermore, we extend our techniques to show that, (softmax-)attention-only layers are capable of approximating various statistical models in-context. We believe these techniques hold independent interest.
On Statistical Rates of Conditional Diffusion Transformers: Approximation, Estimation and Minimax Optimality
Nov 26, 2024



Abstract:We investigate the approximation and estimation rates of conditional diffusion transformers (DiTs) with classifier-free guidance. We present a comprehensive analysis for ``in-context'' conditional DiTs under four common data assumptions. We show that both conditional DiTs and their latent variants lead to the minimax optimality of unconditional DiTs under identified settings. Specifically, we discretize the input domains into infinitesimal grids and then perform a term-by-term Taylor expansion on the conditional diffusion score function under H\"older smooth data assumption. This enables fine-grained use of transformers' universal approximation through a more detailed piecewise constant approximation and hence obtains tighter bounds. Additionally, we extend our analysis to the latent setting under the linear latent subspace assumption. We not only show that latent conditional DiTs achieve lower bounds than conditional DiTs both in approximation and estimation, but also show the minimax optimality of latent unconditional DiTs. Our findings establish statistical limits for conditional and unconditional DiTs, and offer practical guidance toward developing more efficient and accurate DiT models.
Transformers are Deep Optimizers: Provable In-Context Learning for Deep Model Training
Nov 25, 2024


Abstract:We investigate the transformer's capability for in-context learning (ICL) to simulate the training process of deep models. Our key contribution is providing a positive example of using a transformer to train a deep neural network by gradient descent in an implicit fashion via ICL. Specifically, we provide an explicit construction of a $(2N+4)L$-layer transformer capable of simulating $L$ gradient descent steps of an $N$-layer ReLU network through ICL. We also give the theoretical guarantees for the approximation within any given error and the convergence of the ICL gradient descent. Additionally, we extend our analysis to the more practical setting using Softmax-based transformers. We validate our findings on synthetic datasets for 3-layer, 4-layer, and 6-layer neural networks. The results show that ICL performance matches that of direct training.
On Statistical Rates and Provably Efficient Criteria of Latent Diffusion Transformers (DiTs)
Jul 01, 2024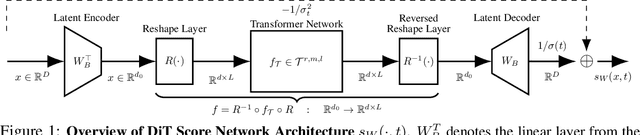
Abstract:We investigate the statistical and computational limits of latent \textbf{Di}ffusion \textbf{T}ransformers (\textbf{DiT}s) under the low-dimensional linear latent space assumption. Statistically, we study the universal approximation and sample complexity of the DiTs score function, as well as the distribution recovery property of the initial data. Specifically, under mild data assumptions, we derive an approximation error bound for the score network of latent DiTs, which is sub-linear in the latent space dimension. Additionally, we derive the corresponding sample complexity bound and show that the data distribution generated from the estimated score function converges toward a proximate area of the original one. Computationally, we characterize the hardness of both forward inference and backward computation of latent DiTs, assuming the Strong Exponential Time Hypothesis (SETH). For forward inference, we identify efficient criteria for all possible latent DiTs inference algorithms and showcase our theory by pushing the efficiency toward almost-linear time inference. For backward computation, we leverage the low-rank structure within the gradient computation of DiTs training for possible algorithmic speedup. Specifically, we show that such speedup achieves almost-linear time latent DiTs training by casting the DiTs gradient as a series of chained low-rank approximations with bounded error. Under the low-dimensional assumption, we show that the convergence rate and the computational efficiency are both dominated by the dimension of the subspace, suggesting that latent DiTs have the potential to bypass the challenges associated with the high dimensionality of initial data.
DNABERT-S: Learning Species-Aware DNA Embedding with Genome Foundation Models
Feb 15, 2024



Abstract:Effective DNA embedding remains crucial in genomic analysis, particularly in scenarios lacking labeled data for model fine-tuning, despite the significant advancements in genome foundation models. A prime example is metagenomics binning, a critical process in microbiome research that aims to group DNA sequences by their species from a complex mixture of DNA sequences derived from potentially thousands of distinct, often uncharacterized species. To fill the lack of effective DNA embedding models, we introduce DNABERT-S, a genome foundation model that specializes in creating species-aware DNA embeddings. To encourage effective embeddings to error-prone long-read DNA sequences, we introduce Manifold Instance Mixup (MI-Mix), a contrastive objective that mixes the hidden representations of DNA sequences at randomly selected layers and trains the model to recognize and differentiate these mixed proportions at the output layer. We further enhance it with the proposed Curriculum Contrastive Learning (C$^2$LR) strategy. Empirical results on 18 diverse datasets showed DNABERT-S's remarkable performance. It outperforms the top baseline's performance in 10-shot species classification with just a 2-shot training while doubling the Adjusted Rand Index (ARI) in species clustering and substantially increasing the number of correctly identified species in metagenomics binning. The code, data, and pre-trained model are publicly available at https://github.com/Zhihan1996/DNABERT_S.
A manifold learning-based CSI feedback framework for FDD massive MIMO
Apr 28, 2023



Abstract:Massive multi-input multi-output (MIMO) in Frequency Division Duplex (FDD) mode suffers from heavy feedback overhead for Channel State Information (CSI). In this paper, a novel manifold learning-based CSI feedback framework (MLCF) is proposed to reduce the feedback and improve the spectral efficiency of FDD massive MIMO. Manifold learning (ML) is an effective method for dimensionality reduction. However, most ML algorithms focus only on data compression, and lack the corresponding recovery methods. Moreover, the computational complexity is high when dealing with incremental data. To solve these problems, we propose a landmark selection algorithm to characterize the topological skeleton of the manifold where the CSI sample resides. Based on the learned skeleton, the local patch of the incremental CSI on the manifold can be easily determined by its nearest landmarks. This motivates us to propose a low-complexity compression and reconstruction scheme by keeping the local geometric relationships with landmarks unchanged. We theoretically prove the convergence of the proposed algorithm. Meanwhile, the upper bound on the error of approximating the CSI samples using landmarks is derived. Simulation results under an industrial channel model of 3GPP demonstrate that the proposed MLCF method outperforms existing algorithms based on compressed sensing and deep learning.
Instance-aware Model Ensemble With Distillation For Unsupervised Domain Adaptation
Nov 15, 2022
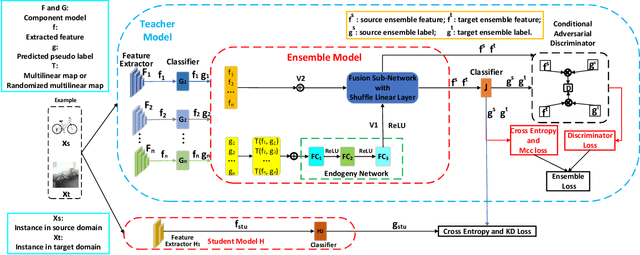
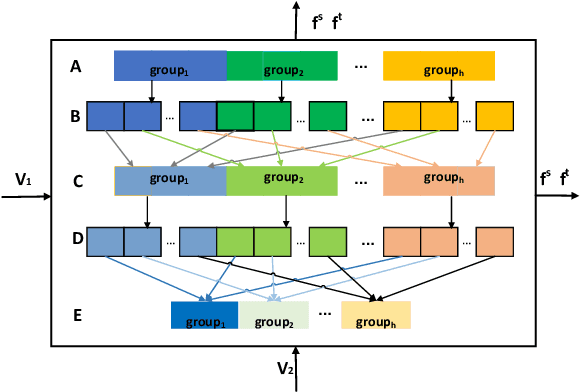
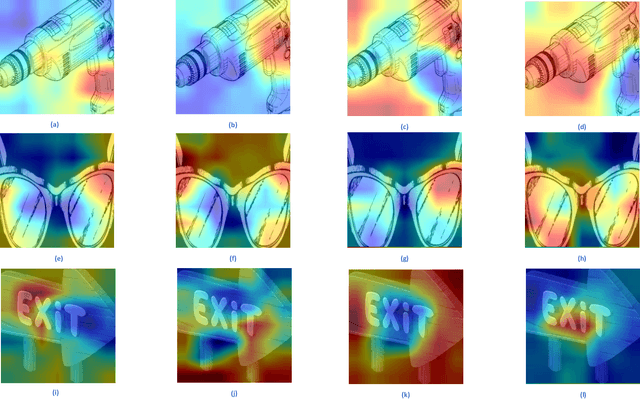
Abstract:The linear ensemble based strategy, i.e., averaging ensemble, has been proposed to improve the performance in unsupervised domain adaptation tasks. However, a typical UDA task is usually challenged by dynamically changing factors, such as variable weather, views, and background in the unlabeled target domain. Most previous ensemble strategies ignore UDA's dynamic and uncontrollable challenge, facing limited feature representations and performance bottlenecks. To enhance the model, adaptability between domains and reduce the computational cost when deploying the ensemble model, we propose a novel framework, namely Instance aware Model Ensemble With Distillation, IMED, which fuses multiple UDA component models adaptively according to different instances and distills these components into a small model. The core idea of IMED is a dynamic instance aware ensemble strategy, where for each instance, a nonlinear fusion subnetwork is learned that fuses the extracted features and predicted labels of multiple component models. The nonlinear fusion method can help the ensemble model handle dynamically changing factors. After learning a large capacity ensemble model with good adaptability to different changing factors, we leverage the ensemble teacher model to guide the learning of a compact student model by knowledge distillation. Furthermore, we provide the theoretical analysis of the validity of IMED for UDA. Extensive experiments conducted on various UDA benchmark datasets, e.g., Office 31, Office Home, and VisDA 2017, show the superiority of the model based on IMED to the state of the art methods under the comparable computation cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge