Solving Trojan Detection Competitions with Linear Weight Classification

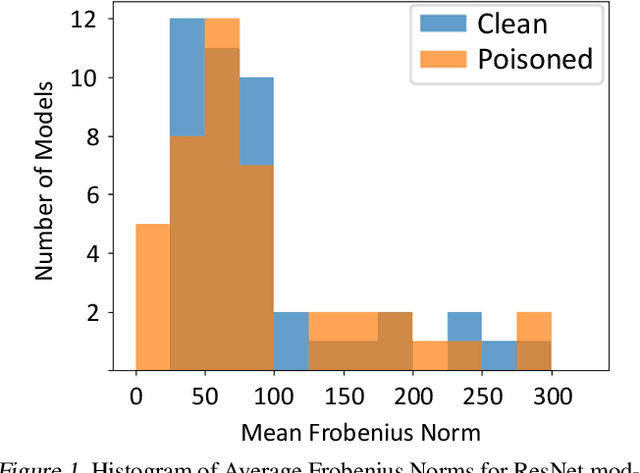
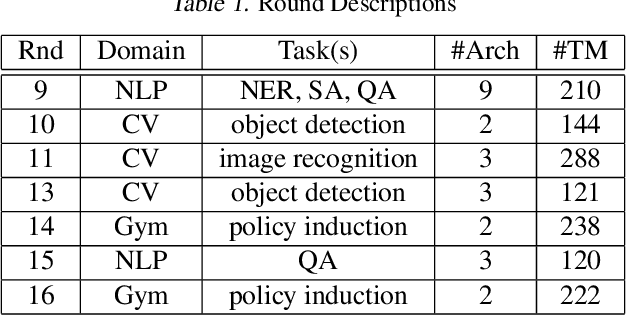
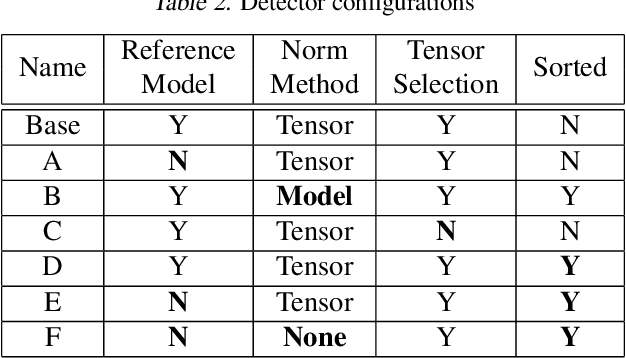
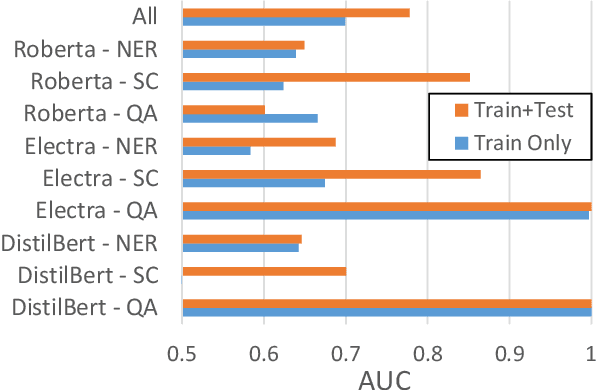
Neural networks can conceal malicious Trojan backdoors that allow a trigger to covertly change the model behavior. Detecting signs of these backdoors, particularly without access to any triggered data, is the subject of ongoing research and open challenges. In one common formulation of the problem, we are given a set of clean and poisoned models and need to predict whether a given test model is clean or poisoned. In this paper, we introduce a detector that works remarkably well across many of the existing datasets and domains. It is obtained by training a binary classifier on a large number of models' weights after performing a few different pre-processing steps including feature selection and standardization, reference model weights subtraction, and model alignment prior to detection. We evaluate this algorithm on a diverse set of Trojan detection benchmarks and domains and examine the cases where the approach is most and least effective.

Privacy Leakage Avoidance with Switching Ensembles

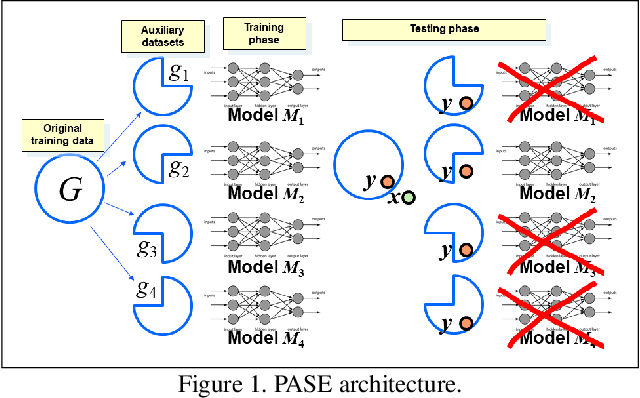
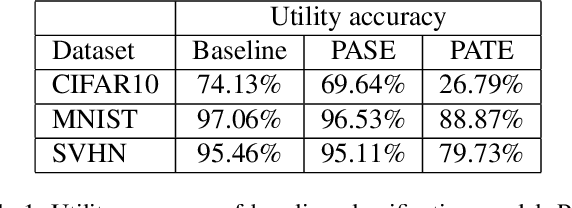
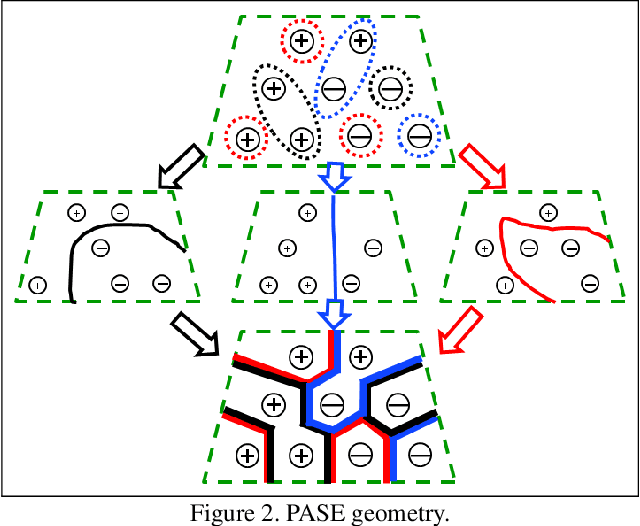
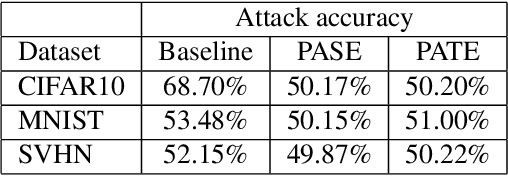
We consider membership inference attacks, one of the main privacy issues in machine learning. These recently developed attacks have been proven successful in determining, with confidence better than a random guess, whether a given sample belongs to the dataset on which the attacked machine learning model was trained. Several approaches have been developed to mitigate this privacy leakage but the tradeoff performance implications of these defensive mechanisms (i.e., accuracy and utility of the defended machine learning model) are not well studied yet. We propose a novel approach of privacy leakage avoidance with switching ensembles (PASE), which both protects against current membership inference attacks and does that with very small accuracy penalty, while requiring acceptable increase in training and inference time. We test our PASE method, along with the the current state-of-the-art PATE approach, on three calibration image datasets and analyze their tradeoffs.

MathQA: Towards Interpretable Math Word Problem Solving with Operation-Based Formalisms

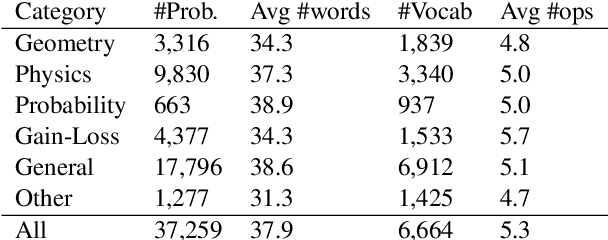
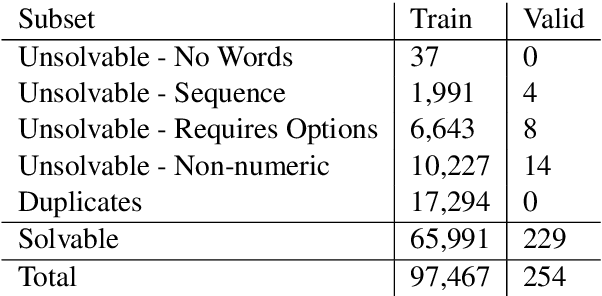
We introduce a large-scale dataset of math word problems and an interpretable neural math problem solver that learns to map problems to operation programs. Due to annotation challenges, current datasets in this domain have been either relatively small in scale or did not offer precise operational annotations over diverse problem types. We introduce a new representation language to model precise operation programs corresponding to each math problem that aim to improve both the performance and the interpretability of the learned models. Using this representation language, our new dataset, MathQA, significantly enhances the AQuA dataset with fully-specified operational programs. We additionally introduce a neural sequence-to-program model enhanced with automatic problem categorization. Our experiments show improvements over competitive baselines in our MathQA as well as the AQuA dataset. The results are still significantly lower than human performance indicating that the dataset poses new challenges for future research. Our dataset is available at: https://math-qa.github.io/math-QA/