Covariates-Adjusted Mixed-Membership Estimation: A Novel Network Model with Optimal Guarantees

This paper addresses the problem of mixed-membership estimation in networks, where the goal is to efficiently estimate the latent mixed-membership structure from the observed network. Recognizing the widespread availability and valuable information carried by node covariates, we propose a novel network model that incorporates both community information, as represented by the Degree-Corrected Mixed Membership (DCMM) model, and node covariate similarities to determine connections. We investigate the regularized maximum likelihood estimation (MLE) for this model and demonstrate that our approach achieves optimal estimation accuracy for both the similarity matrix and the mixed-membership, in terms of both the Frobenius norm and the entrywise loss. Since directly analyzing the original convex optimization problem is intractable, we employ nonconvex optimization to facilitate the analysis. A key contribution of our work is identifying a crucial assumption that bridges the gap between convex and nonconvex solutions, enabling the transfer of statistical guarantees from the nonconvex approach to its convex counterpart. Importantly, our analysis extends beyond the MLE loss and the mean squared error (MSE) used in matrix completion problems, generalizing to all the convex loss functions. Consequently, our analysis techniques extend to a broader set of applications, including ranking problems based on pairwise comparisons. Finally, simulation experiments validate our theoretical findings, and real-world data analyses confirm the practical relevance of our model.

Covariate Assisted Entity Ranking with Sparse Intrinsic Scores

This paper addresses the item ranking problem with associate covariates, focusing on scenarios where the preference scores can not be fully explained by covariates, and the remaining intrinsic scores, are sparse. Specifically, we extend the pioneering Bradley-Terry-Luce (BTL) model by incorporating covariate information and considering sparse individual intrinsic scores. Our work introduces novel model identification conditions and examines the regularized penalized Maximum Likelihood Estimator (MLE) statistical rates. We then construct a debiased estimator for the penalized MLE and analyze its distributional properties. Additionally, we apply our method to the goodness-of-fit test for models with no latent intrinsic scores, namely, the covariates fully explaining the preference scores of individual items. We also offer confidence intervals for ranks. Our numerical studies lend further support to our theoretical findings, demonstrating validation for our proposed method

Inferences on Mixing Probabilities and Ranking in Mixed-Membership Models

Network data is prevalent in numerous big data applications including economics and health networks where it is of prime importance to understand the latent structure of network. In this paper, we model the network using the Degree-Corrected Mixed Membership (DCMM) model. In DCMM model, for each node $i$, there exists a membership vector $\boldsymbol{\pi}_ i = (\boldsymbol{\pi}_i(1), \boldsymbol{\pi}_i(2),\ldots, \boldsymbol{\pi}_i(K))$, where $\boldsymbol{\pi}_i(k)$ denotes the weight that node $i$ puts in community $k$. We derive novel finite-sample expansion for the $\boldsymbol{\pi}_i(k)$s which allows us to obtain asymptotic distributions and confidence interval of the membership mixing probabilities and other related population quantities. This fills an important gap on uncertainty quantification on the membership profile. We further develop a ranking scheme of the vertices based on the membership mixing probabilities on certain communities and perform relevant statistical inferences. A multiplier bootstrap method is proposed for ranking inference of individual member's profile with respect to a given community. The validity of our theoretical results is further demonstrated by via numerical experiments in both real and synthetic data examples.

Uncertainty Quantification of MLE for Entity Ranking with Covariates

This paper concerns with statistical estimation and inference for the ranking problems based on pairwise comparisons with additional covariate information such as the attributes of the compared items. Despite extensive studies, few prior literatures investigate this problem under the more realistic setting where covariate information exists. To tackle this issue, we propose a novel model, Covariate-Assisted Ranking Estimation (CARE) model, that extends the well-known Bradley-Terry-Luce (BTL) model, by incorporating the covariate information. Specifically, instead of assuming every compared item has a fixed latent score $\{\theta_i^*\}_{i=1}^n$, we assume the underlying scores are given by $\{\alpha_i^*+{x}_i^\top\beta^*\}_{i=1}^n$, where $\alpha_i^*$ and ${x}_i^\top\beta^*$ represent latent baseline and covariate score of the $i$-th item, respectively. We impose natural identifiability conditions and derive the $\ell_{\infty}$- and $\ell_2$-optimal rates for the maximum likelihood estimator of $\{\alpha_i^*\}_{i=1}^{n}$ and $\beta^*$ under a sparse comparison graph, using a novel `leave-one-out' technique (Chen et al., 2019) . To conduct statistical inferences, we further derive asymptotic distributions for the MLE of $\{\alpha_i^*\}_{i=1}^n$ and $\beta^*$ with minimal sample complexity. This allows us to answer the question whether some covariates have any explanation power for latent scores and to threshold some sparse parameters to improve the ranking performance. We improve the approximation method used in (Gao et al., 2021) for the BLT model and generalize it to the CARE model. Moreover, we validate our theoretical results through large-scale numerical studies and an application to the mutual fund stock holding dataset.

Distillation $\approx$ Early Stopping? Harvesting Dark Knowledge Utilizing Anisotropic Information Retrieval For Overparameterized Neural Network

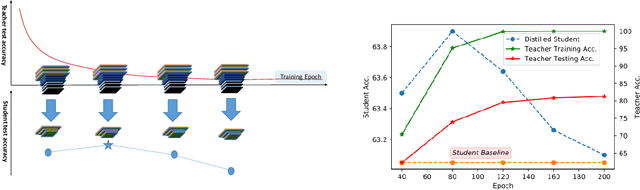
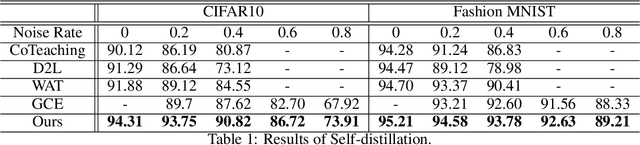
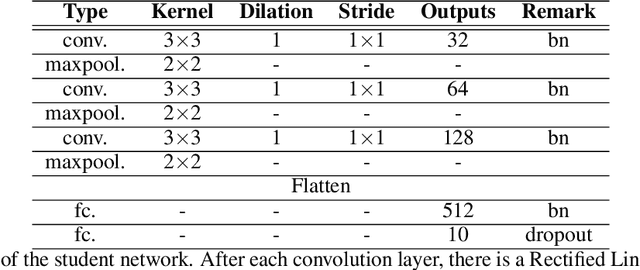
Distillation is a method to transfer knowledge from one model to another and often achieves higher accuracy with the same capacity. In this paper, we aim to provide a theoretical understanding on what mainly helps with the distillation. Our answer is "early stopping". Assuming that the teacher network is overparameterized, we argue that the teacher network is essentially harvesting dark knowledge from the data via early stopping. This can be justified by a new concept, {Anisotropic Information Retrieval (AIR)}, which means that the neural network tends to fit the informative information first and the non-informative information (including noise) later. Motivated by the recent development on theoretically analyzing overparameterized neural networks, we can characterize AIR by the eigenspace of the Neural Tangent Kernel(NTK). AIR facilities a new understanding of distillation. With that, we further utilize distillation to refine noisy labels. We propose a self-distillation algorithm to sequentially distill knowledge from the network in the previous training epoch to avoid memorizing the wrong labels. We also demonstrate, both theoretically and empirically, that self-distillation can benefit from more than just early stopping. Theoretically, we prove convergence of the proposed algorithm to the ground truth labels for randomly initialized overparameterized neural networks in terms of $\ell_2$ distance, while the previous result was on convergence in $0$-$1$ loss. The theoretical result ensures the learned neural network enjoy a margin on the training data which leads to better generalization. Empirically, we achieve better testing accuracy and entirely avoid early stopping which makes the algorithm more user-friendly.

A Gram-Gauss-Newton Method Learning Overparameterized Deep Neural Networks for Regression Problems

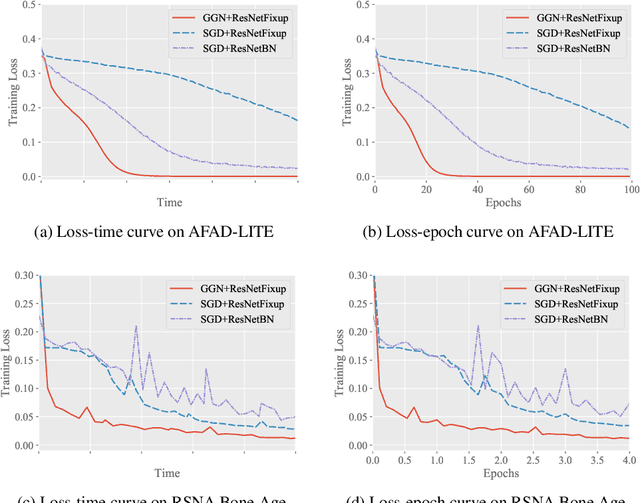
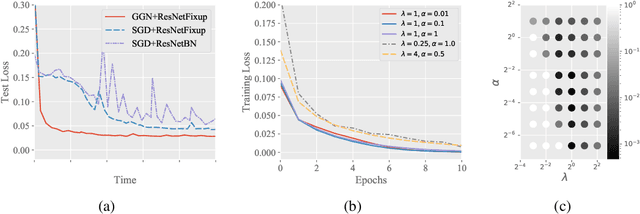
First-order methods such as stochastic gradient descent (SGD) are currently the standard algorithm for training deep neural networks. Second-order methods, despite their better convergence rate, are rarely used in practice due to the prohibitive computational cost in calculating the second order information. In this paper, we propose a novel Gram-Gauss-Newton (GGN) algorithm to train deep neural networks for regression problems with square loss. Different from typical second-order methods that have heavy computational cost in each iteration, our proposed GGN only has minor overhead compared to first-order methods such as SGD. We also provide theoretical results to show that for sufficiently wide neural networks, the convergence rate of the GGN algorithm is quadratic. Preliminary experiments on regression tasks demonstrate that for training standard networks, the GGN algorithm converges faster and achieves better performance than SGD.