A Gram-Gauss-Newton Method Learning Overparameterized Deep Neural Networks for Regression Problems

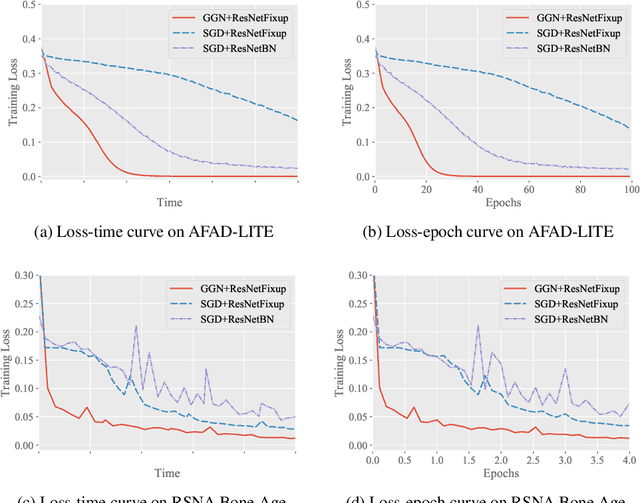
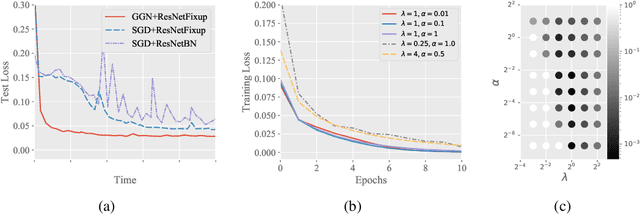
First-order methods such as stochastic gradient descent (SGD) are currently the standard algorithm for training deep neural networks. Second-order methods, despite their better convergence rate, are rarely used in practice due to the prohibitive computational cost in calculating the second order information. In this paper, we propose a novel Gram-Gauss-Newton (GGN) algorithm to train deep neural networks for regression problems with square loss. Different from typical second-order methods that have heavy computational cost in each iteration, our proposed GGN only has minor overhead compared to first-order methods such as SGD. We also provide theoretical results to show that for sufficiently wide neural networks, the convergence rate of the GGN algorithm is quadratic. Preliminary experiments on regression tasks demonstrate that for training standard networks, the GGN algorithm converges faster and achieves better performance than SGD.