Fundamental Computational Limits in Pursuing Invariant Causal Prediction and Invariance-Guided Regularization

Pursuing invariant prediction from heterogeneous environments opens the door to learning causality in a purely data-driven way and has several applications in causal discovery and robust transfer learning. However, existing methods such as ICP [Peters et al., 2016] and EILLS [Fan et al., 2024] that can attain sample-efficient estimation are based on exponential time algorithms. In this paper, we show that such a problem is intrinsically hard in computation: the decision problem, testing whether a non-trivial prediction-invariant solution exists across two environments, is NP-hard even for the linear causal relationship. In the world where P$\neq$NP, our results imply that the estimation error rate can be arbitrarily slow using any computationally efficient algorithm. This suggests that pursuing causality is fundamentally harder than detecting associations when no prior assumption is pre-offered. Given there is almost no hope of computational improvement under the worst case, this paper proposes a method capable of attaining both computationally and statistically efficient estimation under additional conditions. Furthermore, our estimator is a distributionally robust estimator with an ellipse-shaped uncertain set where more uncertainty is placed on spurious directions than invariant directions, resulting in a smooth interpolation between the most predictive solution and the causal solution by varying the invariance hyper-parameter. Non-asymptotic results and empirical applications support the claim.

Causality Pursuit from Heterogeneous Environments via Neural Adversarial Invariance Learning

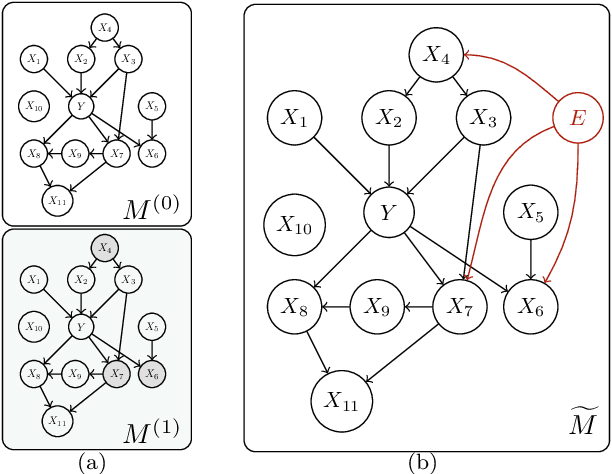
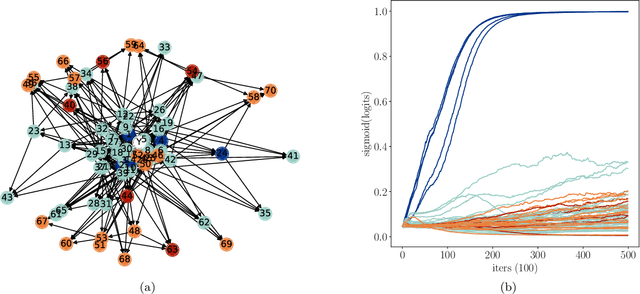
Statistics suffers from a fundamental problem, "the curse of endogeneity" -- the regression function, or more broadly the prediction risk minimizer with infinite data, may not be the target we wish to pursue. This is because when complex data are collected from multiple sources, the biases deviated from the interested (causal) association inherited in individuals or sub-populations are not expected to be canceled. Traditional remedies are of hindsight and restrictive in being tailored to prior knowledge like untestable cause-effect structures, resulting in methods that risk model misspecification and lack scalable applicability. This paper seeks to offer a purely data-driven and universally applicable method that only uses the heterogeneity of the biases in the data rather than following pre-offered commandments. Such an idea is formulated as a nonparametric invariance pursuit problem, whose goal is to unveil the invariant conditional expectation $m^\star(x)\equiv \mathbb{E}[Y^{(e)}|X_{S^\star}^{(e)}=x_{S^\star}]$ with unknown important variable set $S^\star$ across heterogeneous environments $e\in \mathcal{E}$. Under the structural causal model framework, $m^\star$ can be interpreted as certain data-driven causality in general. The paper contributes to proposing a novel framework, called Focused Adversarial Invariance Regularization (FAIR), formulated as a single minimax optimization program that can solve the general invariance pursuit problem. As illustrated by the unified non-asymptotic analysis, our adversarial estimation framework can attain provable sample-efficient estimation akin to standard regression under a minimal identification condition for various tasks and models. As an application, the FAIR-NN estimator realized by two Neural Network classes is highlighted as the first approach to attain statistically efficient estimation in general nonparametric invariance learning.

The Implicit Bias of Heterogeneity towards Invariance and Causality

It is observed empirically that the large language models (LLM), trained with a variant of regression loss using numerous corpus from the Internet, can unveil causal associations to some extent. This is contrary to the traditional wisdom that ``association is not causation'' and the paradigm of traditional causal inference in which prior causal knowledge should be carefully incorporated into the design of methods. It is a mystery why causality, in a higher layer of understanding, can emerge from the regression task that pursues associations. In this paper, we claim the emergence of causality from association-oriented training can be attributed to the coupling effects from the heterogeneity of the source data, stochasticity of training algorithms, and over-parameterization of the learning models. We illustrate such an intuition using a simple but insightful model that learns invariance, a quasi-causality, using regression loss. To be specific, we consider multi-environment low-rank matrix sensing problems where the unknown r-rank ground-truth d*d matrices diverge across the environments but contain a lower-rank invariant, causal part. In this case, running pooled gradient descent will result in biased solutions that only learn associations in general. We show that running large-batch Stochastic Gradient Descent, whose each batch being linear measurement samples randomly selected from a certain environment, can successfully drive the solution towards the invariant, causal solution under certain conditions. This step is related to the relatively strong heterogeneity of the environments, the large step size and noises in the optimization algorithm, and the over-parameterization of the model. In summary, we unveil another implicit bias that is a result of the symbiosis between the heterogeneity of data and modern algorithms, which is, to the best of our knowledge, first in the literature.

Environment Invariant Linear Least Squares

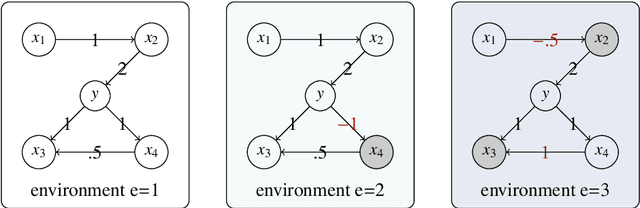
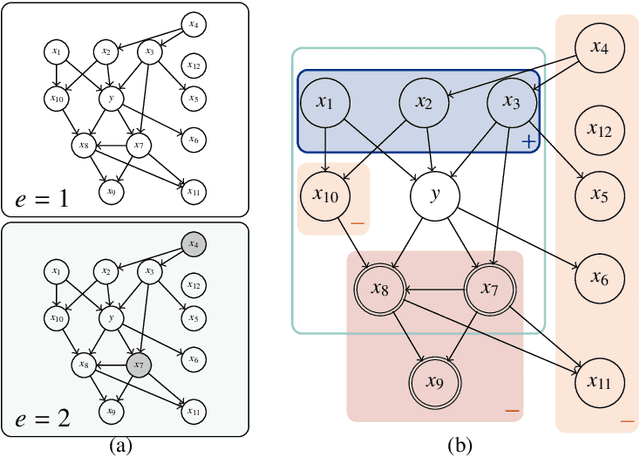
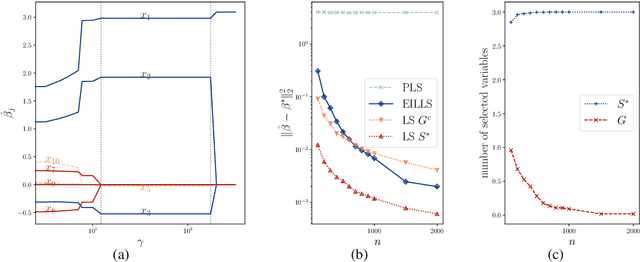
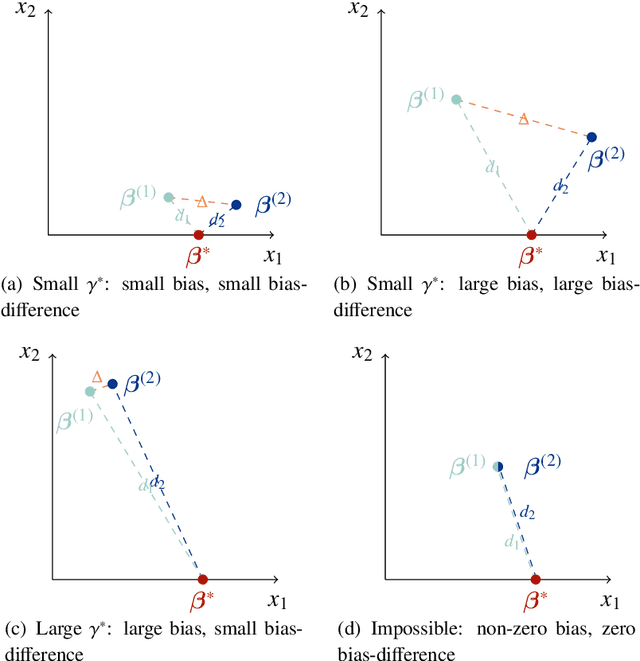
This paper considers a multiple environments linear regression model in which data from multiple experimental settings are collected. The joint distribution of the response variable and covariate may vary across different environments, yet the conditional expectation of $y$ given the unknown set of important variables are invariant across environments. Such a statistical model is related to the problem of endogeneity, causal inference, and transfer learning. The motivation behind it is illustrated by how the goals of prediction and attribution are inherent in estimating the true parameter and the important variable set. We construct a novel {\it environment invariant linear least squares (EILLS)} objective function, a multiple-environment version of linear least squares that leverages the above conditional expectation invariance structure and heterogeneity among different environments to determine the true parameter. Our proposed method is applicable without any additional structural knowledge and can identify the true parameter under a near-minimal identification condition. We establish non-asymptotic $\ell_2$ error bounds on the estimation error for the EILLS estimator in the presence of spurious variables. Moreover, we further show that the EILLS estimator is able to eliminate all endogenous variables and the $\ell_0$ penalized EILLS estimator can achieve variable selection consistency in high-dimensional regimes. These non-asymptotic results demonstrate the sample efficiency of the EILLS estimator and its capability to circumvent the curse of endogeneity in an algorithmic manner without any prior structural knowledge.

How do noise tails impact on deep ReLU networks?

This paper investigates the stability of deep ReLU neural networks for nonparametric regression under the assumption that the noise has only a finite p-th moment. We unveil how the optimal rate of convergence depends on p, the degree of smoothness and the intrinsic dimension in a class of nonparametric regression functions with hierarchical composition structure when both the adaptive Huber loss and deep ReLU neural networks are used. This optimal rate of convergence cannot be obtained by the ordinary least squares but can be achieved by the Huber loss with a properly chosen parameter that adapts to the sample size, smoothness, and moment parameters. A concentration inequality for the adaptive Huber ReLU neural network estimators with allowable optimization errors is also derived. To establish a matching lower bound within the class of neural network estimators using the Huber loss, we employ a different strategy from the traditional route: constructing a deep ReLU network estimator that has a better empirical loss than the true function and the difference between these two functions furnishes a low bound. This step is related to the Huberization bias, yet more critically to the approximability of deep ReLU networks. As a result, we also contribute some new results on the approximation theory of deep ReLU neural networks.

Convex Formulation of Overparameterized Deep Neural Networks

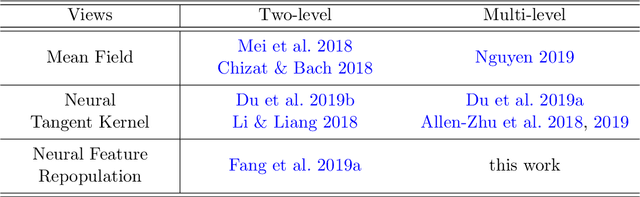
Analysis of over-parameterized neural networks has drawn significant attention in recentyears. It was shown that such systems behave like convex systems under various restrictedsettings, such as for two-level neural networks, and when learning is only restricted locally inthe so-called neural tangent kernel space around specialized initializations. However, there areno theoretical techniques that can analyze fully trained deep neural networks encountered inpractice. This paper solves this fundamental problem by investigating such overparameterizeddeep neural networks when fully trained. We generalize a new technique called neural feature repopulation, originally introduced in (Fang et al., 2019a) for two-level neural networks, to analyze deep neural networks. It is shown that under suitable representations, overparameterized deep neural networks are inherently convex, and when optimized, the system can learn effective features suitable for the underlying learning task under mild conditions. This new analysis is consistent with empirical observations that deep neural networks are capable of learning efficient feature representations. Therefore, the highly unexpected result of this paper can satisfactorily explain the practical success of deep neural networks. Empirical studies confirm that predictions of our theory are consistent with results observed in practice.

Cross Domain Imitation Learning

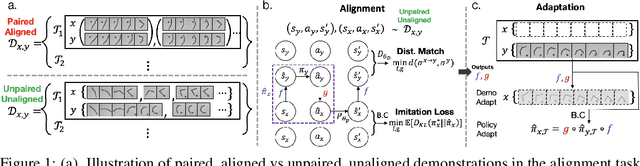
We study the question of how to imitate tasks across domains with discrepancies such as embodiment and viewpoint mismatch. Many prior works require paired, aligned demonstrations and an additional RL procedure for the task. However, paired, aligned demonstrations are seldom obtainable and RL procedures are expensive. In this work, we formalize the Cross Domain Imitation Learning (CDIL) problem, which encompasses imitation learning in the presence of viewpoint and embodiment mismatch. Informally, CDIL is the process of learning how to perform a task optimally, given demonstrations of the task in a distinct domain. We propose a two step approach to CDIL: alignment followed by adaptation. In the alignment step we execute a novel unsupervised MDP alignment algorithm, Generative Adversarial MDP Alignment (GAMA), to learn state and action correspondences from unpaired, unaligned demonstrations. In the adaptation step we leverage the correspondences to zero-shot imitate tasks across domains. To describe when CDIL is feasible via alignment and adaptation, we introduce a theory of MDP alignability. We experimentally evaluate GAMA against baselines in both embodiment and viewpoint mismatch scenarios where aligned demonstrations don't exist and show the effectiveness of our approach.

Language Modeling with Sparse Product of Sememe Experts

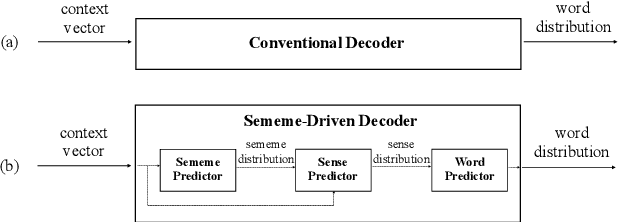
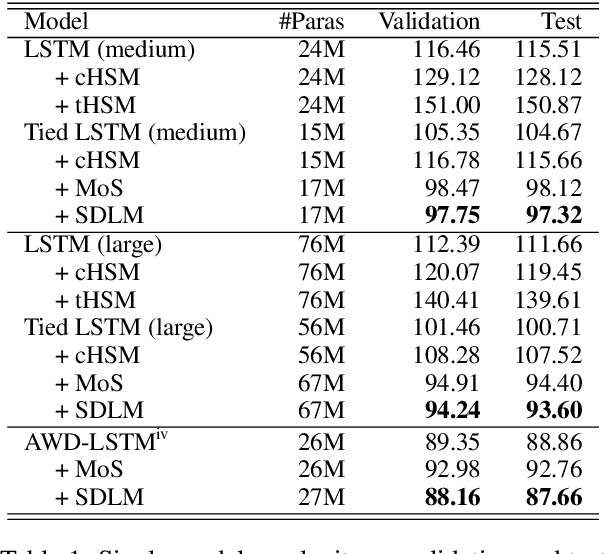
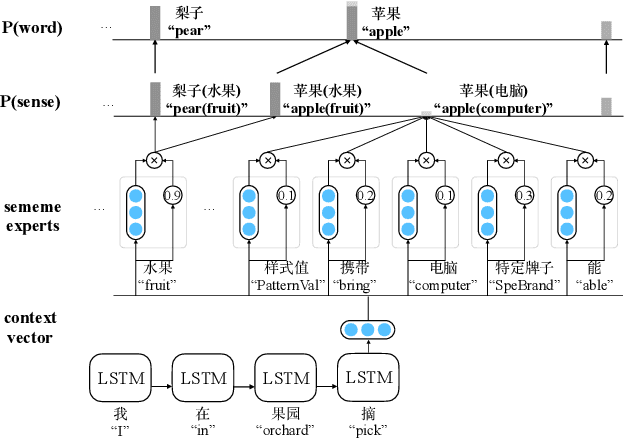
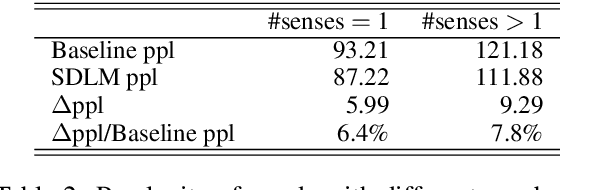
Most language modeling methods rely on large-scale data to statistically learn the sequential patterns of words. In this paper, we argue that words are atomic language units but not necessarily atomic semantic units. Inspired by HowNet, we use sememes, the minimum semantic units in human languages, to represent the implicit semantics behind words for language modeling, named Sememe-Driven Language Model (SDLM). More specifically, to predict the next word, SDLM first estimates the sememe distribution gave textual context. Afterward, it regards each sememe as a distinct semantic expert, and these experts jointly identify the most probable senses and the corresponding word. In this way, SDLM enables language models to work beyond word-level manipulation to fine-grained sememe-level semantics and offers us more powerful tools to fine-tune language models and improve the interpretability as well as the robustness of language models. Experiments on language modeling and the downstream application of headline gener- ation demonstrate the significant effect of SDLM. Source code and data used in the experiments can be accessed at https:// github.com/thunlp/SDLM-pytorch.

ZhuSuan: A Library for Bayesian Deep Learning

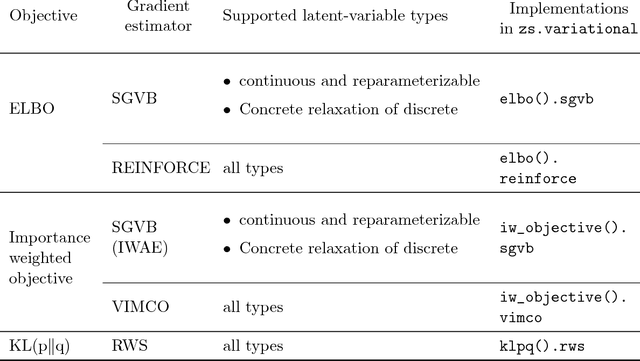
In this paper we introduce ZhuSuan, a python probabilistic programming library for Bayesian deep learning, which conjoins the complimentary advantages of Bayesian methods and deep learning. ZhuSuan is built upon Tensorflow. Unlike existing deep learning libraries, which are mainly designed for deterministic neural networks and supervised tasks, ZhuSuan is featured for its deep root into Bayesian inference, thus supporting various kinds of probabilistic models, including both the traditional hierarchical Bayesian models and recent deep generative models. We use running examples to illustrate the probabilistic programming on ZhuSuan, including Bayesian logistic regression, variational auto-encoders, deep sigmoid belief networks and Bayesian recurrent neural networks.