Convex Formulation of Overparameterized Deep Neural Networks
Paper and Code
Nov 18, 2019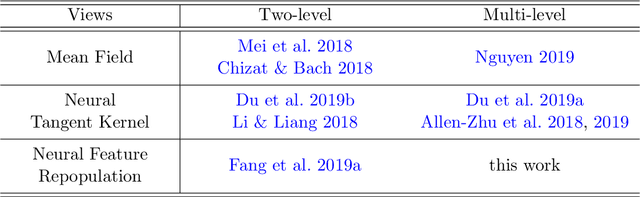



Analysis of over-parameterized neural networks has drawn significant attention in recentyears. It was shown that such systems behave like convex systems under various restrictedsettings, such as for two-level neural networks, and when learning is only restricted locally inthe so-called neural tangent kernel space around specialized initializations. However, there areno theoretical techniques that can analyze fully trained deep neural networks encountered inpractice. This paper solves this fundamental problem by investigating such overparameterizeddeep neural networks when fully trained. We generalize a new technique called neural feature repopulation, originally introduced in (Fang et al., 2019a) for two-level neural networks, to analyze deep neural networks. It is shown that under suitable representations, overparameterized deep neural networks are inherently convex, and when optimized, the system can learn effective features suitable for the underlying learning task under mild conditions. This new analysis is consistent with empirical observations that deep neural networks are capable of learning efficient feature representations. Therefore, the highly unexpected result of this paper can satisfactorily explain the practical success of deep neural networks. Empirical studies confirm that predictions of our theory are consistent with results observed in practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge