Environment Invariant Linear Least Squares

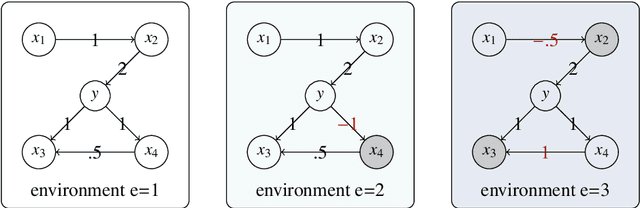
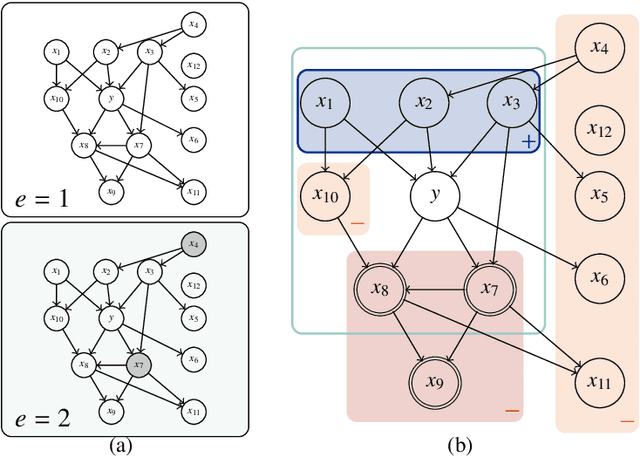
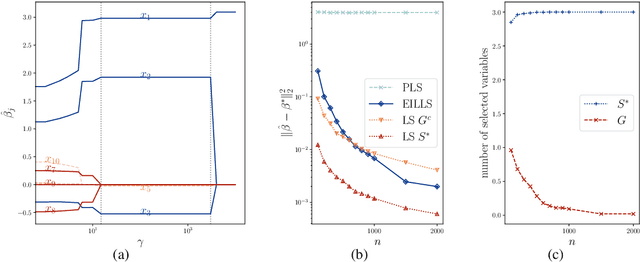
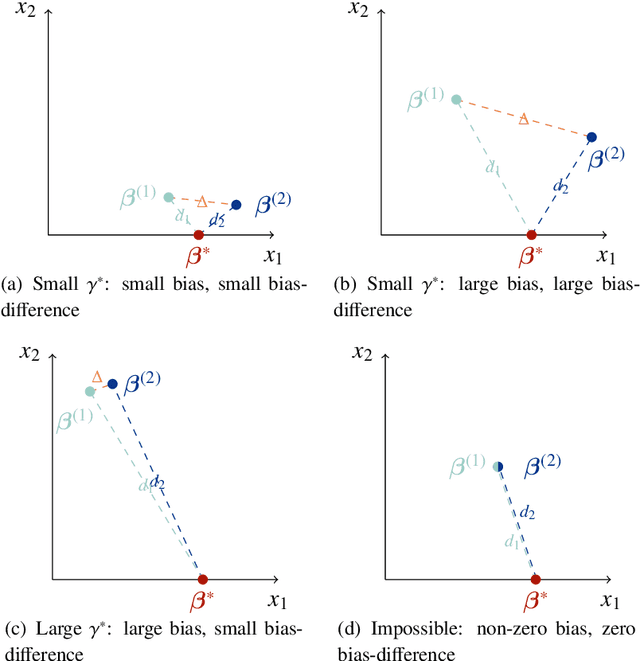
This paper considers a multiple environments linear regression model in which data from multiple experimental settings are collected. The joint distribution of the response variable and covariate may vary across different environments, yet the conditional expectation of $y$ given the unknown set of important variables are invariant across environments. Such a statistical model is related to the problem of endogeneity, causal inference, and transfer learning. The motivation behind it is illustrated by how the goals of prediction and attribution are inherent in estimating the true parameter and the important variable set. We construct a novel {\it environment invariant linear least squares (EILLS)} objective function, a multiple-environment version of linear least squares that leverages the above conditional expectation invariance structure and heterogeneity among different environments to determine the true parameter. Our proposed method is applicable without any additional structural knowledge and can identify the true parameter under a near-minimal identification condition. We establish non-asymptotic $\ell_2$ error bounds on the estimation error for the EILLS estimator in the presence of spurious variables. Moreover, we further show that the EILLS estimator is able to eliminate all endogenous variables and the $\ell_0$ penalized EILLS estimator can achieve variable selection consistency in high-dimensional regimes. These non-asymptotic results demonstrate the sample efficiency of the EILLS estimator and its capability to circumvent the curse of endogeneity in an algorithmic manner without any prior structural knowledge.